最近线性代数学了行化简算法解矩阵方程，老师布置课后思考题要我们用代码实现解线性方程组QwQ。所以今天就让我们一同学习一些高斯消元和约旦消元两种解线性方程组的方法吧！

线性方程组和增广矩阵

首先，什么是线性方程呢？我们定义形如a1x1+a2x2+……+anxn=b的方程为线性方程，即每个未知数的次数都是一次的方程我们称为线性方程。那什么是线性方程组呢？顾名思义，就是由一个或多个线性方程组成的方程组，其大致形式如下：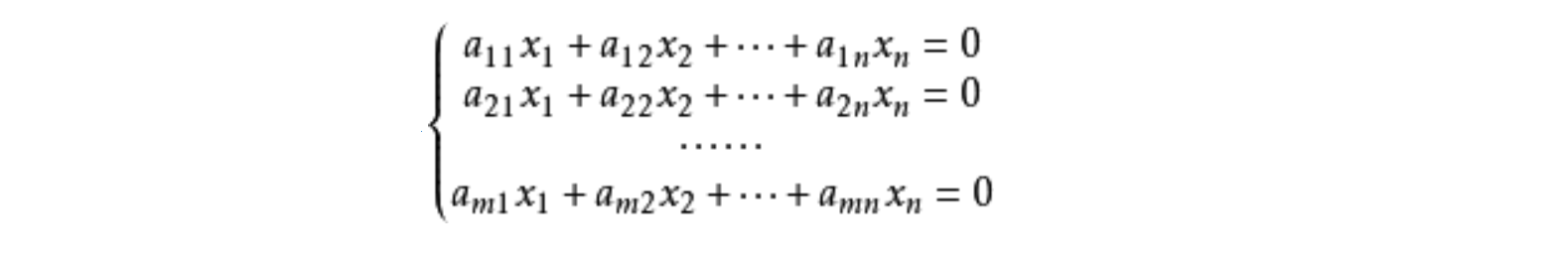
举个例子吧，如下图，左边为线性方程组，右边为非线性方程组：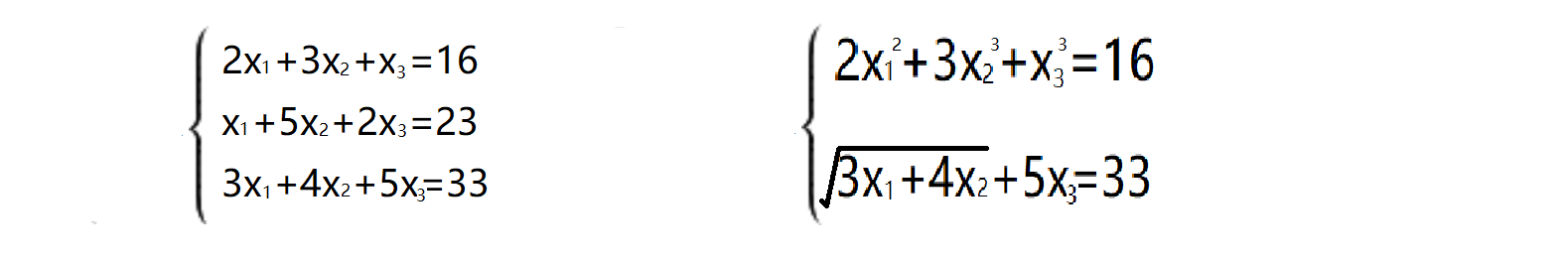

那么我们什么是增广矩阵呢？我们把包括常数项的线性方程组的每一项的系数抽取出来，组成的矩阵，就是增广矩阵，如下：

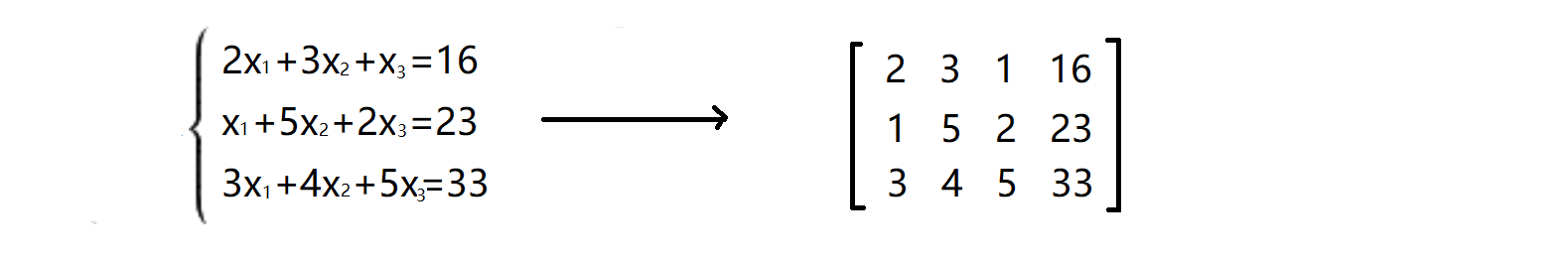
如上图，在方程组中我们知道若将三个方程分别标记为①②③，则下面三种操作不会改变方程组的解：

1.交换任意两个线性方程；
2.将一个线性方程两边都乘以一个不为0的数；
3.将一个线性方程替换为自己的一个非0倍数和方程组中另一个线性方程的和；

同样的变换成矩阵后，相应地，下面三种操作也不会改变矩阵所对应的线性方程组的解：

1.交换任意两行；
2.将矩阵的一行同时乘以一个不为0的数；
3.将矩阵的一行替换为自己的一个非0倍数和矩阵中另一行的和；

上述变化我们称之为初等行变化。

接着通过消元法我们希望矩阵能变成：

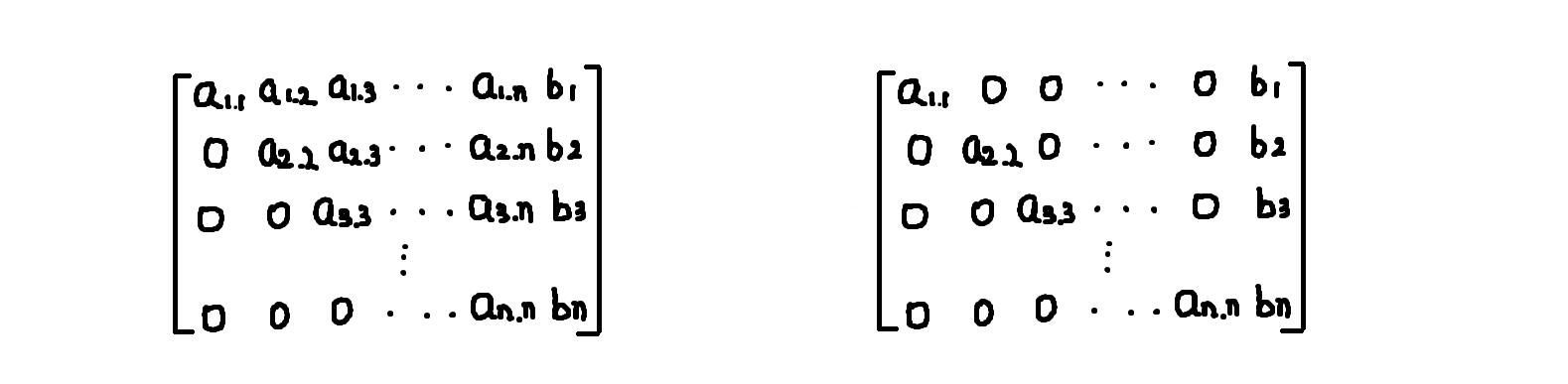
在上述左图中，我们可以先解出第n行的an，接着带回第n-1行解出an-1……以从类推就能解出a1-an了。对于上述右图，就更简单了，对于第i行，左边只剩下了ai*xi，右边剩下bi，所以xi=bi / ai（ai≠0）。此时当ai＝0的的时候，若bi也等于0，那么xi取任何值方程都成立，此时方程有多组解，我们也称xi为自由元；若bi≠0，那么就出现了0＝bi的情况，显然此时方程组无解。

那么如何将增广矩阵化简为上述两种矩阵呢？下面就让我们分别学习两种矩阵的化简方法——高斯消元法和约旦消元法。

高斯消元法

算法思路

高斯消元法的目标就是把增广矩阵化简为上述两种矩阵中左图的那种阶梯型矩阵，也叫上三角矩阵，并解出方程组：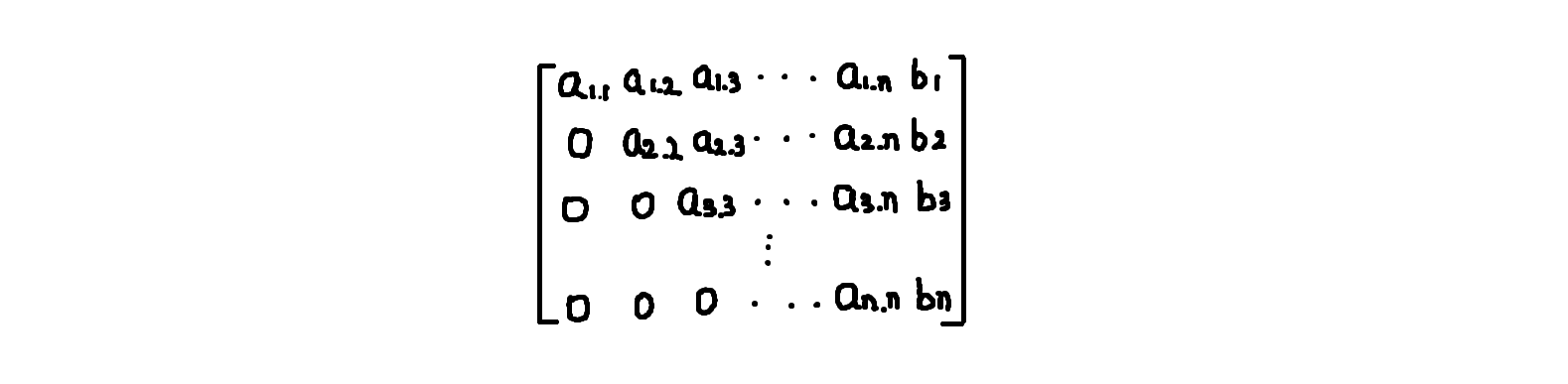
那么我们具体怎么操作呢？其实一共分为4步：

1.从左到右枚举第i列(即枚举主元列)[只枚举线性方程组中未知数的那几列即1-n-1列]，判断第i列上的系数是否全为0，若是，则方程无解或存在多解，跳过看下一列；
2.寻找第i列中系数绝对值最大的一行，将其与第i行交换，保证第i行第i列不为0（即保证主元系数不为0）；
3.通过初等行变化(即减去第i行的某个倍数)，我们将第i+1行到第n行的第i列都变成0；
4.从底向上一步一步带回求解。

这样我们就能把增广矩阵化简为阶梯型矩阵，进而求出方程组的解，下面我们来举个例子吧，假如我们开始时有个普通的增广矩阵，我们设ri表示第i行：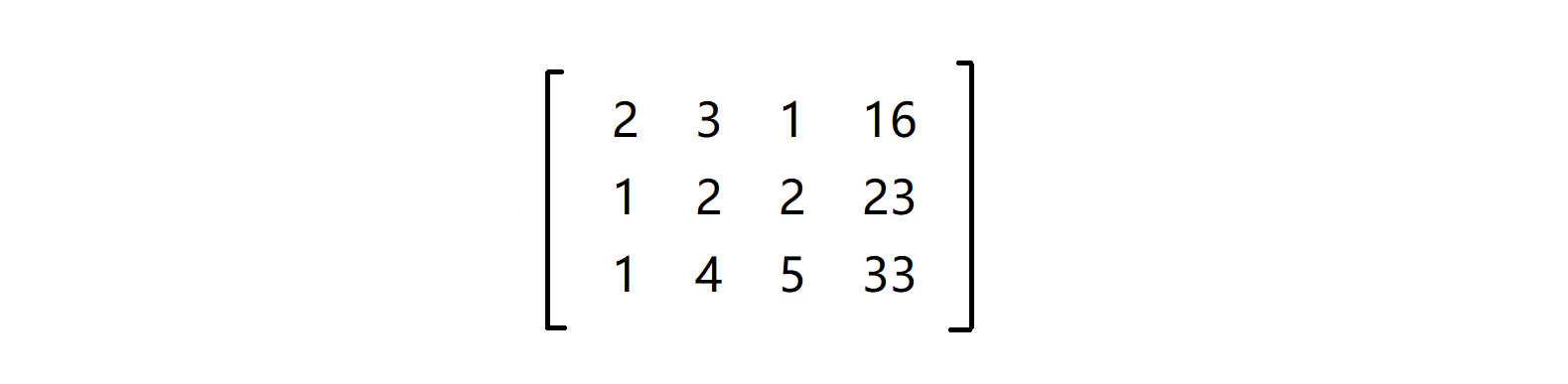

枚举到第一列时，我们发现第一行系数最大，不需要调换，接着把第二行到第三行的第一列系数都变为0：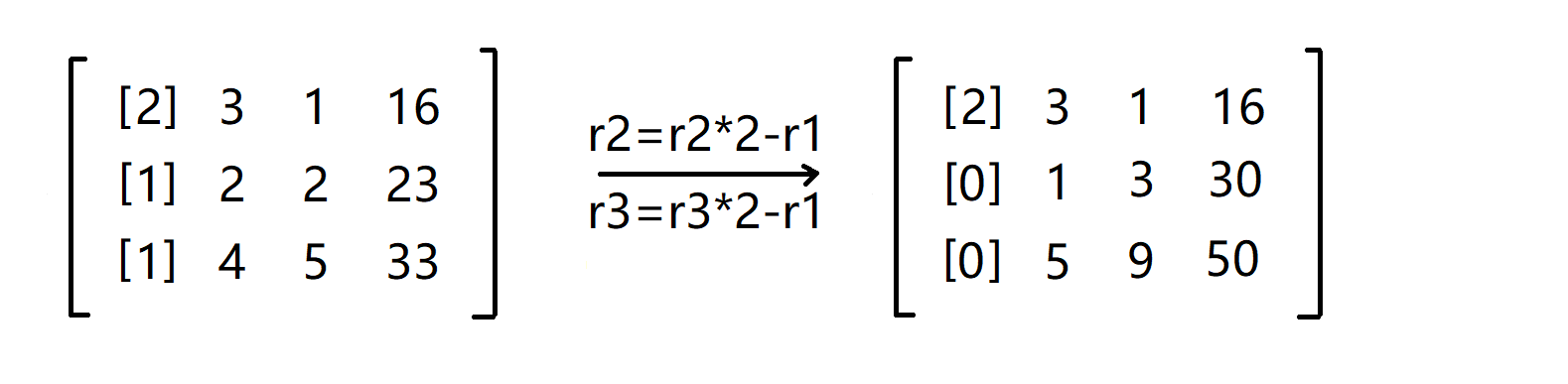

枚举到第二列时，我们发现第三行系数最大，这时我们交换二，三行，接着把第三行的第二列系数变为0：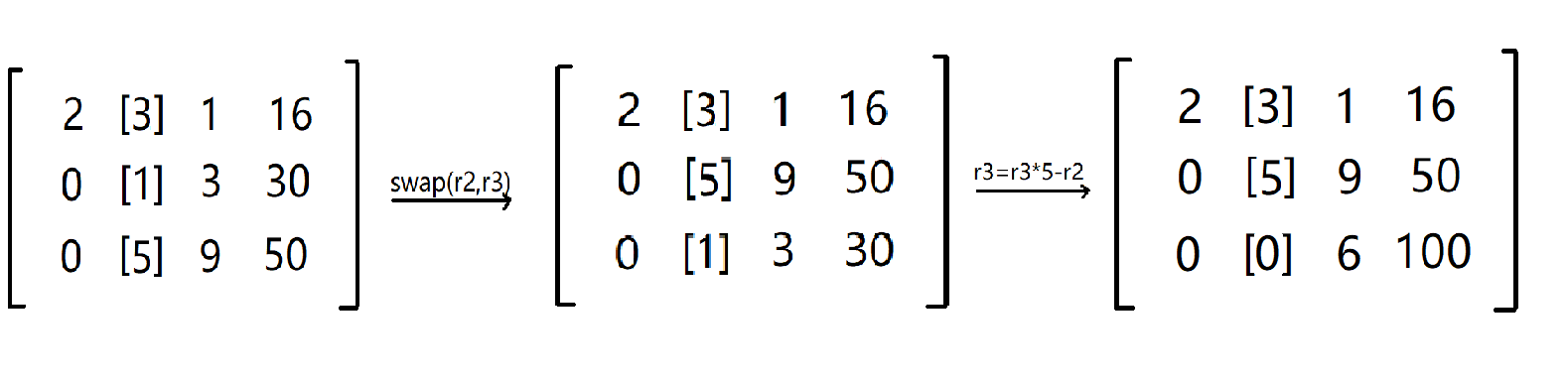

枚举第三列时我们发现已经到最后一行了，枚举的也是最后一个未知数x3的系数了，这时直接自底向上求解出方程组的解：

到这里，高斯消元就做完了！

程序实现

为了方便起见，我们的程序以这道模板题为例子：

经典例题[luogu p3389]

题目背景
Gauss消元

题目描述
给定一个线性方程组，对其求解

输入格式
第一行，一个正整数 n

第二至 n+1行，每行 n+1 个整数，为a1, a2, ……, an和 b，代表一组方程。

输出格式
共n行，每行一个数，第i行为 xi（保留2位小数）

如果不存在唯一解或无解，在第一行输出"No Solution".

输入输出样例
输入 #1
3
1 3 4 5
1 4 7 3
9 3 2 2

输出 #1
-0.97
5.18
-2.39

高斯消元模板

这就是解线性方程组的模板题，直接贴上板子：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
int n, m, js, jl, jk, maxnum, maxline, flag=0;
double a[110][110], multi, ans[110], num;
const double EPS=1e-7;//精度处理 
int main() {
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= n + 1; j++)
            scanf("%lf", &a[i][j]);
    }//读入线性方程组 

    for(int i = 1; i <= n; i++) {//从左到右枚举第i列(即枚举主元列)
        maxnum=0;maxline=0;
        for(int j = i; j <= n; j++) {
            if(fabs(a[j][i]) > maxnum) {
                maxnum = fabs(a[j][i]);
                maxline = j;
            }
        }
        //寻找第i列中系数绝对值最大的一行
        //其与第i行交换，保证第i行第i列不为0（即保证主元系数不为0）；

        if(maxnum < EPS) {
            flag = 1;
            break;
            //判断第i列上的系数是否全为0，若是，则方程无解或存在多解
            //直接特判flag=1输出"No Solution"
        }

        swap(a[i], a[maxline]);
        for(int j = i+1; j <= n; j++) {
            if(a[j][i] == 0)continue;
            else multi = a[j][i]/a[i][i];
            for(int k = i; k <= n + 1; k++) {
                a[j][k] -= a[i][k] * multi;
            }
        }
        //通过初等行变化(即减去第i行的某个倍数)，我们将第i+1行到第n行的第i列都变成0； 
    }

    if(flag == 1) {
        printf("No Solution");
        exit(0);
    }

    for(int i = n; i >= 1; i--) {
        num = a[i][n + 1];
        for(int j = i + 1; j <= n; j++)num -= a[i][j] * ans[j];
        ans[i] = num / a[i][i]; 
    }
    //从底向上一步一步带回求解 

    for(int i = 1; i <=n; i++)printf("%0.2lf\n", ans[i]);
    return 0;
} 

约旦消元法

算法思路

不同于高斯消元法，约旦消元法的目标就是把增广矩阵化简为上述两种矩阵中右图的那种简化阶梯型矩阵，也叫标准型矩阵，并解出方程组：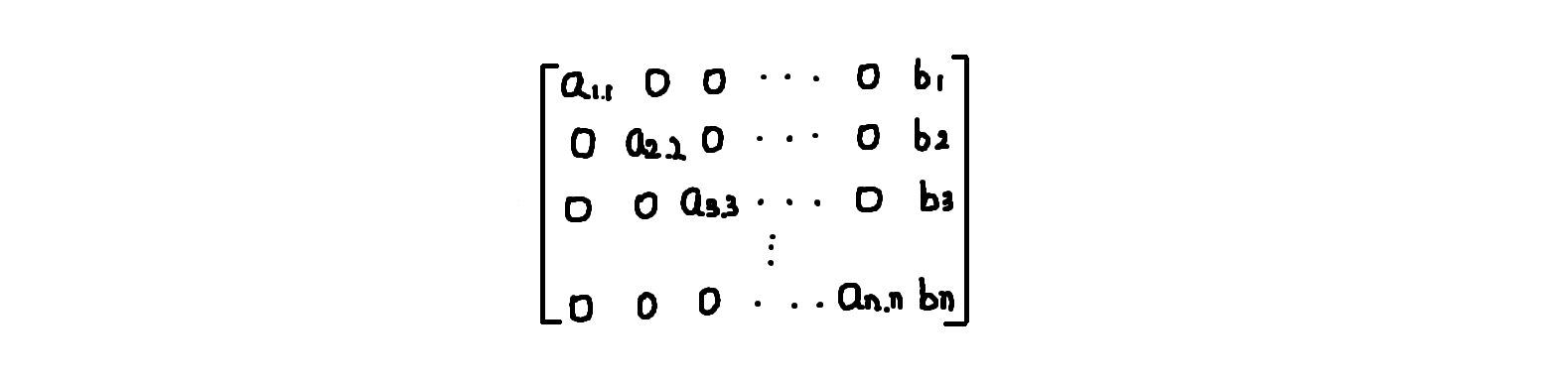

和高斯消元相似地，其步骤其实一共也分为4步：

1.从左到右枚举第i列(即枚举主元列)[只枚举线性方程组中未知数的那几列即1-n-1列]，判断第i列上的系数是否全为0，若是，则方程无解或存在多解，跳过看下一列；
2.寻找第i列中系数绝对值最大的一行，将其与第i行交换，保证第i行第i列不为0（即保证主元系数不为0）；
3.通过初等行变化(即减去第i行的某个倍数)，我们将除去第i行外的第1行到第n行的第i列都变成0，即每一行只留第i个系数(不包含b)；
4.直接求出每个未知数的值。

那么为什么可以通过初等行变化(即减去第i行的某个倍数)，将除去第i行外的第1行到第n行的第i列都变成0呢？我们想，在处理第i列的时候，前i-1列都只有一个系数不为0的元素，换句话说，第i行前i-1个元素都为0，所以对其他列加减一个第i行的某个倍数，是不会破坏之前i-1列每一列的系数的(已决定元素加减一个0*k，无影响)。

下面我们还是举个例子来说明吧，假如我们开始时还是那个普通的增广矩阵，我们设ri表示第i行：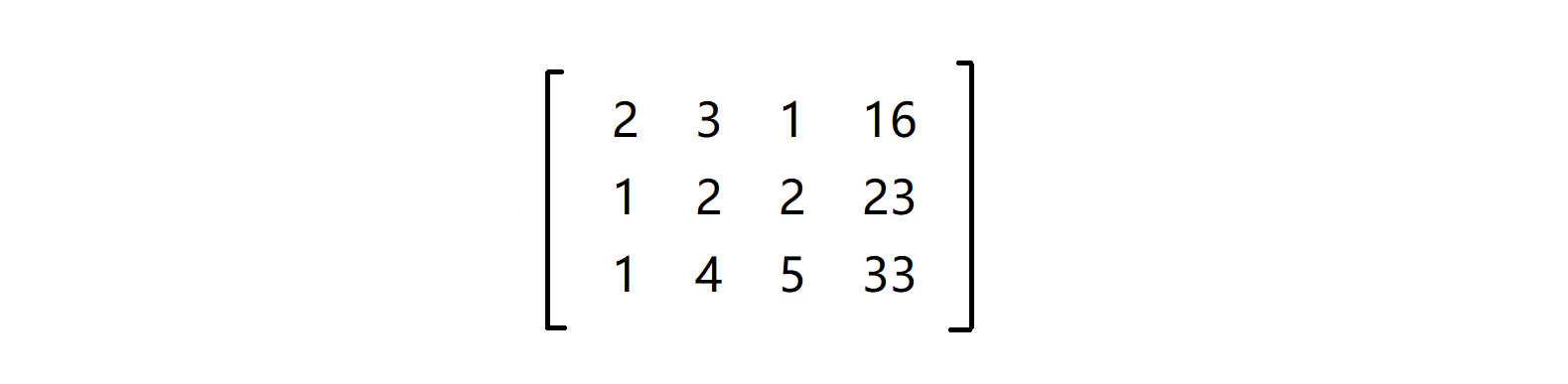

枚举到第一列时，我们发现第一行系数最大，不需要调换，接着把除第一行的第一列系数都变为0：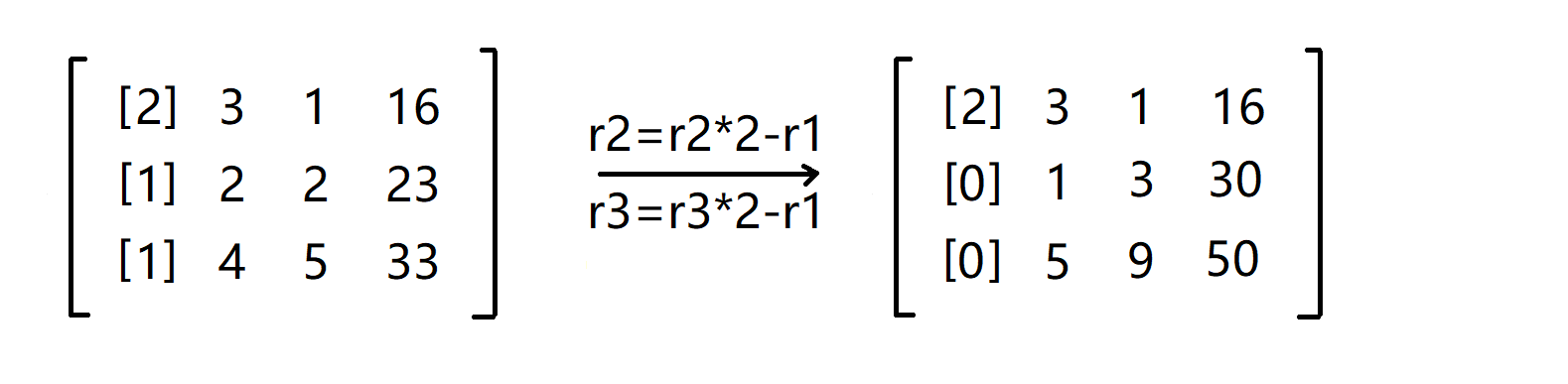

枚举到第二列时，我们发现第三行系数最大，这时我们交换二，三行，接着把除第二行外的第二列系数变为0：

枚举第三列时我们发现已经到最后一行了，枚举的也是最后一个未知数x3的系数了，这时我们把把除第三行外的第三列系数变为0后直接求解出方程组的解：

到这里，约旦消元就做完了！

程序实现

为了方便起见，我们的程序以这道模板题为例子：

经典例题[luogu p3389]

题目背景
Gauss消元

题目描述
给定一个线性方程组，对其求解

输入格式
第一行，一个正整数 n

第二至 n+1行，每行 n+1 个整数，为a1, a2, ……, an和 b，代表一组方程。

输出格式
共n行，每行一个数，第i行为 xi（保留2位小数）

如果不存在唯一解或无解，在第一行输出"No Solution".

输入输出样例
输入 #1
3
1 3 4 5
1 4 7 3
9 3 2 2

输出 #1
-0.97
5.18
-2.39

约旦消元模板

这就是解线性方程组的模板题，直接贴上板子：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
int n, m, js, jl, jk, maxnum, maxline, flag=0;
double a[110][110], multi, ans[110], num;
const double EPS=1e-7;//精度处理 
int main() {
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= n + 1; j++)
            scanf("%lf", &a[i][j]);
    }//读入线性方程组 

    for(int i = 1; i <= n; i++) {//从左到右枚举第i列(即枚举主元列)
        maxnum=0;maxline=0;
        for(int j = i; j<=n; j++) {
            if(fabs(a[j][i]) > maxnum) {
                maxnum = fabs(a[j][i]);
                maxline = j;
            }
        }
        //寻找第i列中系数绝对值最大的一行
        //其与第i行交换，保证第i行第i列不为0（即保证主元系数不为0）；
        if(maxnum < EPS) {
            flag = 1;
            break;
        }
        //判断第i列上的系数是否全为0，若是，则方程无解或存在多解
        //直接特判flag=1输出"No Solution"

        swap(a[i], a[maxline]);
        for(int j = 1; j <= n; j++) {
            if(j != i) {
                if(a[j][i] == 0)continue;
                else multi= a[j][i] / a[i][i];
                for(int k = i; k <= n+1; k++) {
                    a[j][k] -= a[i][k] * multi;
                }
            }
        }
        //通过初等行变化(即减去第i行的某个倍数)，我们将除第i行的第i列都变成0；
    }

    if(flag == 1) {
        printf("No Solution");
        exit(0);
    }

    for(int i = n; i >= 1; i--) {
        ans[i] = a[i][n+1] / a[i][i]; 
    }//直接算出答案 

    for(int i = 1; i <=n; i++)printf("%0.2lf\n", ans[i]);

    return 0;
} 

一些常见问题

Q1：方程无解怎么判断呢？
若你得到一行 0 0 0 0 …… 0 b(b≠0），
那就无解了！

Q2：方程多解是什么情况？
若你得到一行 0 0 0 0 …… 0 b(b＝0），
那么就出现了自由元（不受约束自由取值的未知数），
自由元的个数等于除常数列全部外为0的列数，
这样就多解了！

Q3：方程唯一解长什么样？
就是完美的，标准的上述两种矩阵。

Q4：如何解异或方程组？
例如经典的开关问题，
使用的思想不变，转化的矩阵边也一样，只不过通常只有0，1了，
但消元变成异或消元（1 xor 1=0），
若要解变量i，则找一个i不为0的移动到当前行，用其他不为0的与其异或，进而转化为上述两种矩阵，进而求解。
解的个数：2^n（n为自由元的个数）【自由元再自由在这也只能取0和1】

结语

通过这篇BLOG，相信你已经对线性代数有了初步的了解，也学会了如何求解线性方程组。最后希望你喜欢这篇BLOG！