这周做了新加入的ACCMM协会的热身赛的题目,真的都非常有意思啊,(就是被各路大佬吊锤QWQ),下面就让我们一起来看看吧。
A.Ziyin写作业
题目部分
题目描述:
输入格式:
输出格式:
输入样例:
5 2
1 0
-1 0
0 0
-1 0
1 0输出样例:
1
解题思路
这题作为这套题目的签到题还是有点意思的。首先一个很显然的做法就是两边for循环,枚举所有可能的点积,但是这样做的时间复杂度是 O(n^2), 是无法在时限内通过1e5的数据的,所以我们考虑一下最大值有什么性质。
仔细阅读样例解释我们发现,进行点积的两个向量可以选取同一个向量,那么通过我们发现最大值一定是某个向量i自身与自身的点积(即 i * i)。这是为什么呢,我们用反证法,见下图: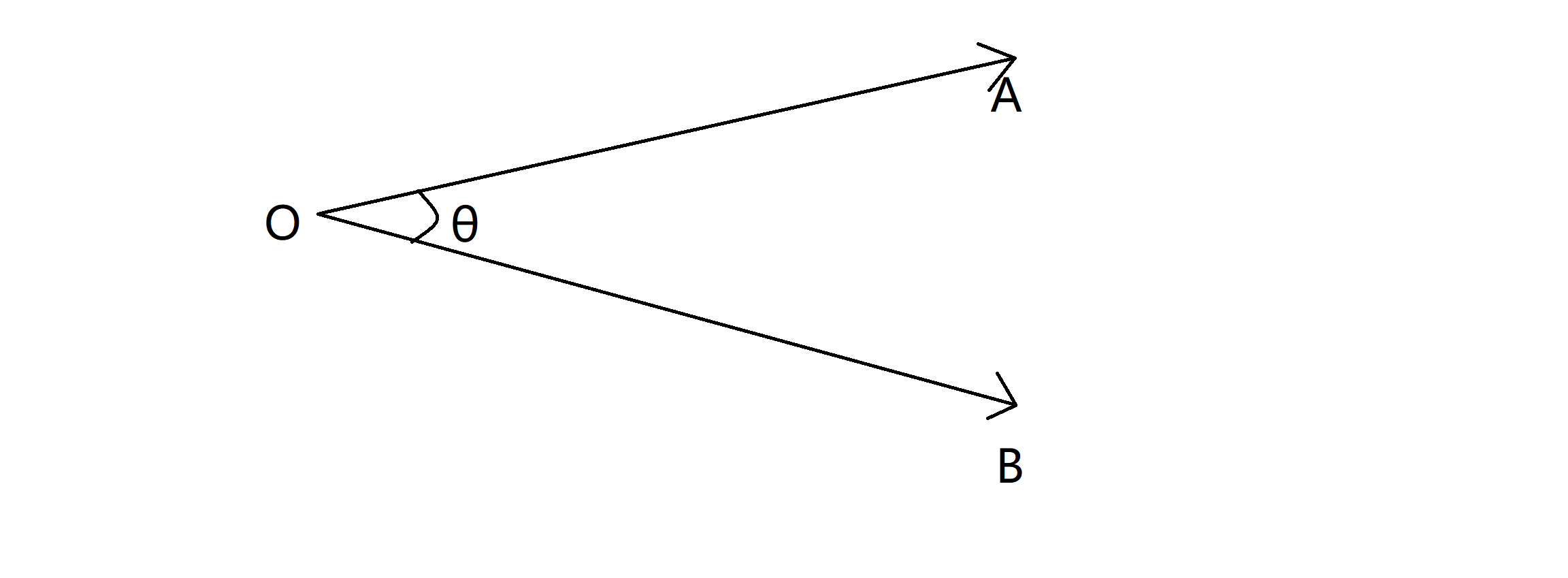
假设我们存在两个不相等的向量A和B,它们的点积是整个向量集里面最大的。设他们的夹角为θ,两向量各自的长度分别为|A|和|B|,则他们点积 X = |A|*|B|*Cosθ。由于Cosθ<=1,那么问题就出现了:
1.若 |A|=|B|,则|A||A| = |B||B| >= |A||B|Cosθ;
2.若 |A|>|B|,则|A||A| >= |A||B|Cosθ;
3.若|B|>|A|,则|B||B| >= |A||B|Cosθ;
即无论如何,当A和B不相同时,都存在某向量与自身的点积,使得其大于等于A和B的点积。所以最大值一定是某个向量i自身与自身的点积。
所以题目就变得很简单了,直接循环一遍,取每个向量与自身点积的最大值就是答案。
代码实现
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
int n, m;
int a[110];
int main() {
long long max_num = 0, jl;
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) {
jl = 0;
for(int j = 1; j <= m; j++) {
scanf("%d", &a[j]);
jl += a[j] * a[j];
}
max_num = max(max_num, jl);
}
printf("%lld\n", max_num);
return 0;
}B.谁去洗碗
题目部分
题目描述:
输入格式:
输出格式:
输入样例:
3 2输出样例:
No
解题思路
这是一道经典的巴什博奕(Bash Game)的题目,其题目原先就是只有一堆n个物品,两个人轮流从这堆物品中取物,规定每次至少取一个,最多取m个。最后取光者得胜。
这类题目我们一般我们从结束状态往前推。显然,如果n=m+1,那么由于一次最多只能取m个,所以,无论先取者拿走多少个,后取者都能够一次拿走剩余的物品,后者取胜。因此我们发现了如何取胜的法则:如果n=(m+1)r+s,(r为任意自然数,s≤m),那么先取者要拿走s个物品,如果后取者拿走k(k≤m)个,那么先取者再拿走m+1-k个,结果剩下(m+1)*(r-1)个,以后保持这样的取法,那么先取者肯定获胜。总之,要保持给对手留下(m+1)的倍数,就能最后获胜。
即若n=k*(m+1),则后取着胜,反之,存在先取者获胜的取法,换言之只有n%(m+1)==0. 先取者才必败。
这种游戏还可以有一种变相的玩法:两个人轮流报数,每次至少报一个,最多报十个,谁能报到100者胜,其实也就等价于从一堆100个石子中取石子,最后取完的胜。所以代码实现就很简单啦。
程序实现
#include<stdio.h>
int main() {
int n, k;
scanf("%d%d", &n, &k);
if(n % (k + 1) == 0) printf("No\n");
else printf("Yes\n");
return 0;
}C.Ziyin的报复
题目部分
题目描述:
输入格式:
输出格式:
输入样例:
3输出样例:
2
解题思路
这又是一道伯努利-欧拉装错信封问题,其递推公式很简单,就是f[0]=1,f[1]=0,f[i]=(f[i-1]+f[i-2])*(i-1) (i>=2)。至于证明和推到过程,我在之前的BLOG当中已经进行过研究了,还不了解的同学可以点击这里!
程序实现
#include<stdio.h>
int main() {
long long f[110000];
int i, n;
scanf("%d", &n);
f[0] = 1; f[1] = 0;
for(i = 2; i <= n; i++) {
f[i] = ((f[i - 1] + f[i - 2]) * (i - 1)) % 998244353;
}
printf("%lld\n", f[n]);
return 0;
}D.Ziyin的数学课
题目部分
题目描述:
输入格式:
输出格式:
输入样例:
3 2输出样例:
6
解题思路
我们对于n,设 a1,a2,……,am 为其全部约数,∑ai 为全部约数的和,∑1/ai 为全部约数的倒数的和,那么我们有:

所以答案就是 n = a * b。
程序实现
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
const double EPS = 1e-6;
int a, b, n, tot, sum;
int num[110];double cum;
int main() {
scanf("%d%d", &a, &b);
printf("%d\n", a * b);
return 0;
}E.Zayin学化学
题目部分
题目描述:
输入格式:
输出格式:
输入样例:
5输出样例:
3
解题思路
这题也算是一道经典题吧,我们首先可以想到的是,只要确定了前n - 1瓶中有没有硫酸钠以及哪一瓶是,第n瓶也就确定了,所以我们实际上只需要考虑前n - 1瓶试剂。我们考虑,对于任一装置,只有产生沉淀和不产生沉淀两种情况,所以想到二进制,考虑到在二进制中确定一个数,就是要知道它的int(log2(n-1)) + 1个二进制位(然后想到类似于字典树贪心解异或题的操作思路(划掉)),所以很显然答案应该是int(log2(n-1)) + 1。那我们要怎么操作呢?
方便起见,假如我们现在 n - 1 = 1000。我们先给1000个瓶分别标上如下标签(10位长度):
0000000001 (第1瓶)
0000000010 (第2瓶)
0000000011 (第3瓶)
.
1111101000 (第1000瓶)
接着从编号最后1位是1的所有的瓶子里面取出1滴混在一起(比如从第一瓶,第三瓶……里分别取出一滴混在一起)并标上记号为1;编号倒数第二位是1的所有的瓶子里面取出1滴混在一起……(比如从第二瓶,第三瓶……里分别取出一滴混在一起)并标上记号为2……以此类推……直到从编号第一位是1的所有的瓶子里面取出1滴混在一起并标上记号为10.现在我们得到了得到有10个编号的混合液,我们将它们编号从小到大按从左到右的顺序排序,并分别给它们滴氯化钡,然后我们观察现象:
从左到右,出现了白色沉淀贴上标签1,没出现白色沉淀的贴上0,最后得到一个序号,把这个序号从右到左的二进制序列换成十进制的数字,就是含有硫酸钠试剂的编号。
检验一下:假如第三瓶有硫酸钠,0000000011 (第3瓶),则第1号和第2号混合液有毒,因此组成的二进制序列为00000011(编号为1,2的试管出现白色沉淀),0000000011二进制序列转换成十进制=3号瓶有硫酸铵。
所以当有int(log2(n-1)) + 1个装置时,就一定可以确定,所以答案就是 n - 1 的二进制序列的长度。
程序实现
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
using namespace std;
int n, ans = 0;
int main() {
scanf("%d", &n);
n--;
while(n > 0) {
ans++;
n /= 2;
}
printf("%d\n", ans);
return 0;
}结语
作为一次热身训练,这次的题目质量非常好,在码量不大的前提下对思维又有着一定的锻炼。现在我将这份题分享给你,最后喜欢你喜欢这篇BLOG!





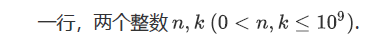



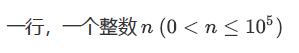
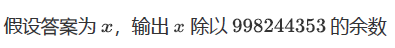


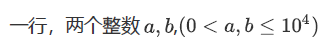






公蒻太强了,毫无几何知识的小蒟蒻过来膜拜Orz
tql
T3 还可以构造递推矩阵用矩阵快速幂O(logn)下求解
T5 我当时是想着就是二分法找假硬币,把每一次的分情况的每一次测量都作为一个机器,即每个机器都有两种情况下的部分,如此来看机器数就是ceil(logn/log2)
cum
tql