上次写完叉积之后感觉意犹未尽，就耗尽了我蒟蒻的所有智商，又去学习了一下二维凸包，发现和叉积一样不(nan)是(dao)太(tu)难(xie)，至于为什么不搞三维凸包......因为搞不来啊:sob:

什么是凸包

首先，什么是凸包问题？
在一个平面上有n个点，过某些点做一个多边形能把所有点“包”起来，当这个多边形是凸多边形时，我们就把它叫做“凸包”，如下图：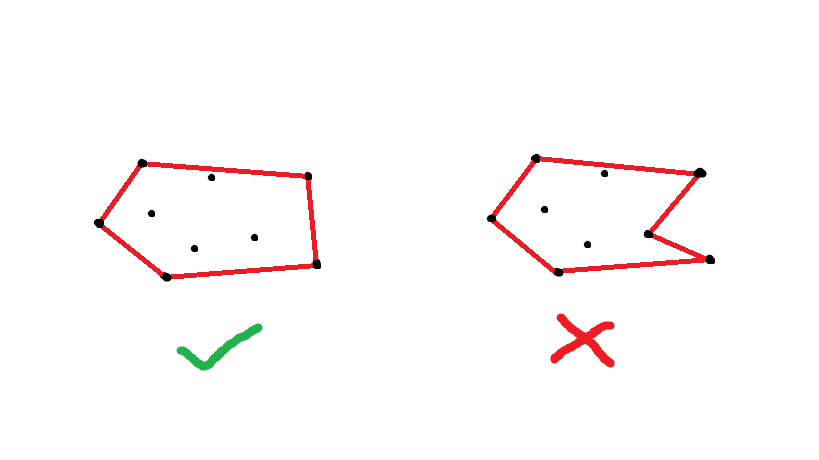
我们把这些点放在二维坐标系中，那么每个点都能用坐标（x，y）表示，现给出点的数量及坐标，求构成凸包的点？

这一类要在二维平面中求解凸包的问题就称为是二维凸包问题。

要怎么求解

在这篇博客中，我会介绍四种解法，难度由浅入深，复杂度也由大到小，下面就让我先来介绍这几种方法：

【一】暴力穷举法

我们都知道两点确定一条直线，这样，我们只需要暴力枚举任意两个点连成一条直线，若其他点都在这条直线的同一侧，那么这两个点就一定是构成凸包上的点，反之就不是。
即这个算法分两步进行：

1.将点两两配对，连成直线
2.对于每条直线，检查剩余（n-2）个点，看是否在直线的同一侧

总的时间复杂度为O(n^3)[n为点的数量]

剩下的问题就是，如何判断剩余点是否在直线的同一侧，让我来介绍一种算法，设p1(x1,y1),p2(x2,y2),p3(x3,y3)，如何判断p3在直线p1，p2的哪一边呢？其实很简单利用上个博客讲到的差积可以推导出计算公式：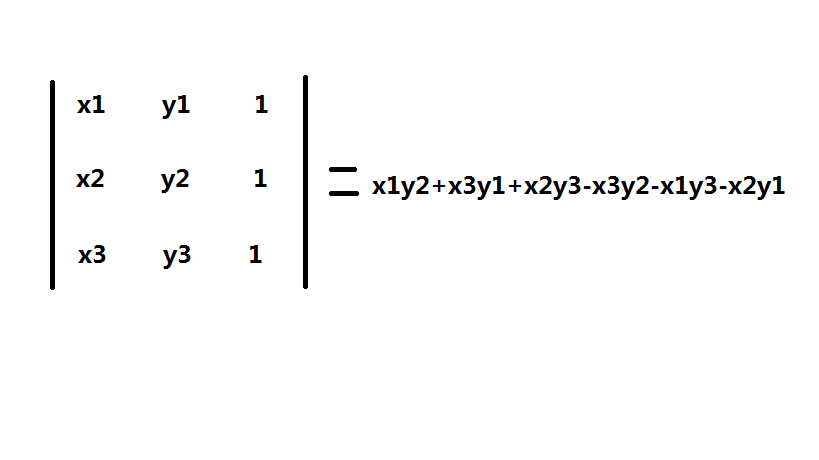
当上式为正时，p3在直线p1p2(即向量p1p2)的左侧
当上式为负时，p3在直线p1p2(即向量p1p2)的右侧
通过以上方法，就可以在O(n^3)的复杂度里求解凸包问题。

【二】分治法

分治法顾名思义就是分而治之，就是把大问题细分为几个小问题进而进行求解，思路其实就是把大凸包不断切成小凸包进行操作，具体步骤如下：

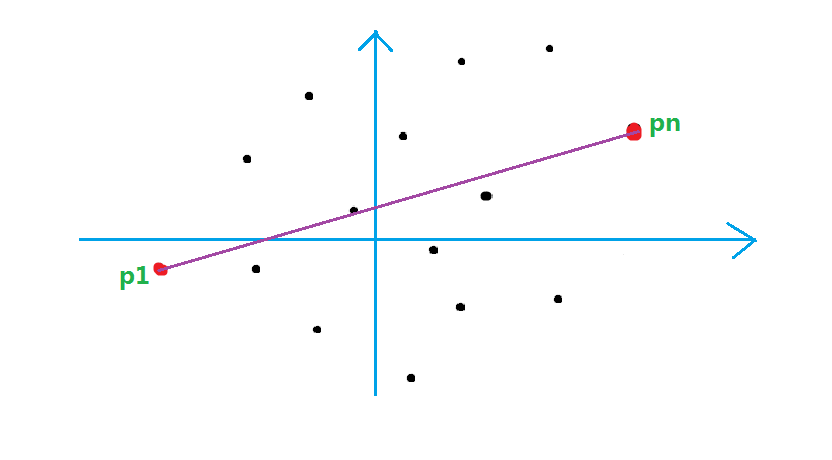
1.把所有点放在二维坐标系中，最左和最右的两个点一定是凸包上的点，分别设为p1 和 pn
2.连接p1、pn，直线P1Pn把点集分为两部分，叫做上包和下包

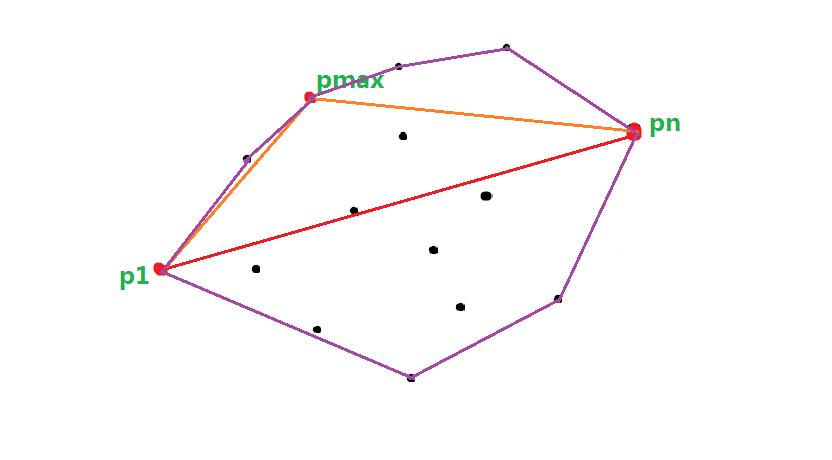
3.对于上包，寻找距离直线p1pn最远的点，设这个点为pmax，做直线P1Pmax，PnPmax,把直线P1Pmax左侧当成上包，把直线PnPmax也当成上包，重复2.3.，对下包也做类似操作即可（如下图）

所以总的时间复杂度为O(nH).[H为凸包上点的个数]
又剩下一个问题了，怎么计算一个点p3到直线P1P2的距离了？这里还是要用到叉积，用到上面的公式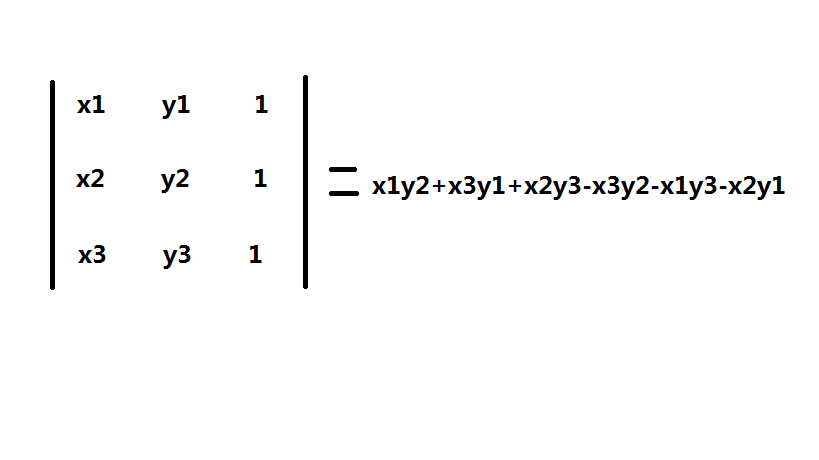其实对结果取绝对值，则绝对值越大，那么点p3到直线P1P2的距离就越大。

【PS】特别需要注意的是，在操作1.中，若横坐标最小的不止一个，那么这些点都是凸包上的点，此时，上包和下包的划分有所不同，需要特别注意。

【三】Jarvis步进法

首先纵坐标最小的点(p0)一定是凸包上的点，从p0开始，按照逆时针方向，逐个找凸包上的点，每次前进一步到下一个点，所以叫步进法。

那么怎么找下一个点？这时我们就要利用向量间的夹角了。如下图，假设现在已经找到了前三个点{p0，p1，p2}了，要找到下一个点，只需在剩下的点中枚举点pi，分别和p2组成向量P2Pi，设这个向量和P1P2的夹角为β，当β最小时就是要求的下一个点了，此处为p3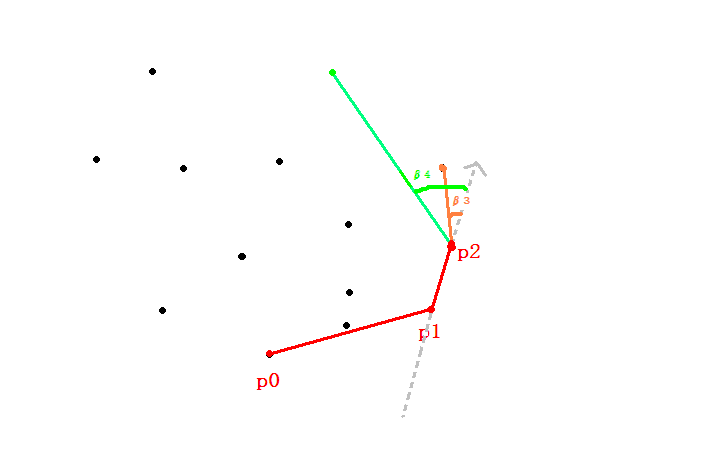

所以总的时间复杂度为O(nH).[H为凸包上点的个数]
剩下的问题就是，如何求β的大小呢？相信大家都学过了平面向量，那么很明显有

【PS】 1.从p0找p1时，通过比较P0Pi与水平线的夹角α的大小，求出α最小的点即为p1.
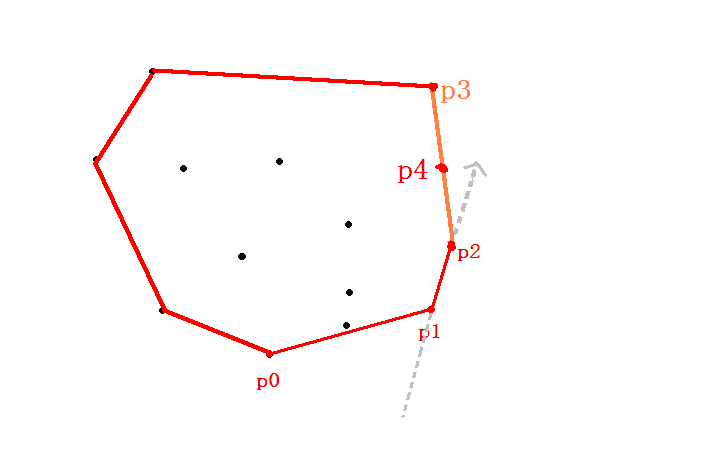
2.当出现三点或以上共线的情况该怎么办？如果p2，p3上还有一点p4，此时三点共线，则p3，p4都为构成凸包的点，并用距离p2最远的点p3作为最后搜索的点，继续找它下一个连接点.(如下图)

【四】Graham扫描法(附模板)

这是在稳定的凸包中很快的算法了，时间复杂度达到了O(nlogn)，我们重点讲解这种神奇的凸包算法。这个算法分为三个部分进行：

1.寻找点集中最下方的点。由于最下方的点一定在凸包上，所以我们可以选取这个点作为起始点（你一定要选最上方我也不拦你）。为了找到这个点，只要在读入的时候判断一下,把我们找到的点放到数组开始（也就是p【1】的位置）就可以了（PS.如果最下的点不止一个，就选取最左边的那个）对应代码如下：

    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",&p[i].x,&p[i].y);
        if(p[i].y<p[1].y ||(p[i].y==p[1].y && p[i].x<p[1].x))
        {
            node t=p[1];p[1]=p[i];p[i]=t;
        }//找最下方的点 
    }

2.对所有点进行快排，但当然不是简单的快排了，所以要写个自定义比较器cmp。那么我们到底要对什么快排呢？没错，就是对p1与剩下点的连线的斜率进行排序，这样做也顺便可以求出第二个凸包上的点（因为斜率最小的那个点也一定在凸包上），排好序的点如下图：
代码如下，其中multi为上次讲到的叉积：

double multi(node p1,node p2, node p0)
{
    double x1=p1.x-p0.x;
    double y1=p1.y-p0.y; 

    double x2=p2.x-p0.x;
    double y2=p2.y-p0.y;

    return(x1*y2-x2*y1); 
}//计算叉积 

bool cmp(node p1,node p2)
{
    int tt=multi(p1,p2,p[1]);
    //当tt＜0时，p2在p1的顺时针方向，所以p2与起始点的斜率小于p1
    if(tt<0)return(0);
    if(tt==0 && dis(p1,p[1])>dis(p2,p[1]))return(0);
    return(1);
}

3.通过上面的操作，我们以及确定了凸包上的前两个点p【1】和p【2】，接下来我们只要按顺序枚举剩下的点，判断剩下的点是否是凸包上的点就行了，同时不要忘记凸包由p【1】开始，由p【1】结束，所以要在p数组的末尾加上p【1】就行了。附上代码：

void graham()
{
    sort(p+2,p+n+1,cmp);
    for(int i=1;i<=2;i++)sta[i]=p[i];
    top=2;
    n++;p[n]=p[1];

    for(int i=3;i<=n;i++)
    {
        while(top>1 && multi(sta[top],p[i],sta[top-1])<=0)top--;
        top++;
        sta[top]=p[i];

    }
}

什么，你看不懂上面这段代码？没事，我们用之前的例子来具体讲讲第三步：

首先，sta数组表示哪些点是凸包上的点，top表示sta数组现在有多少个点。通过1.2.，我们先确定了p1，p2为凸包上的点；

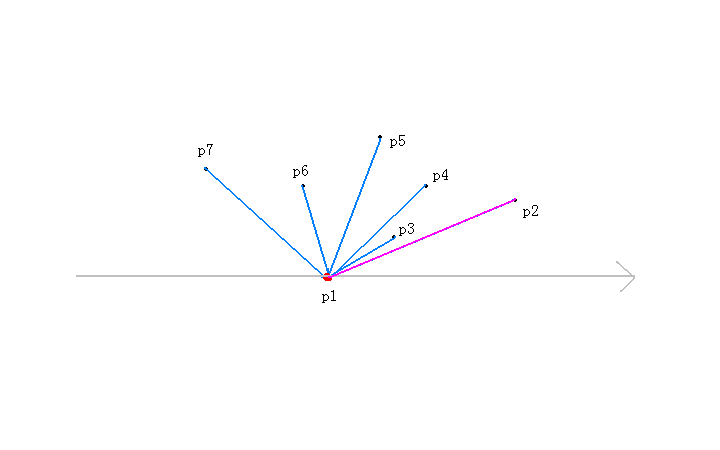
接着我们试着加入第三个点，进入while循环

然后我们对于p【top-1】也就是p【1】来说，p【top】也就是p【2】到p【3】为逆时针，所以multi大于0,不执行top--操作，

加入p【3】这个点。也就是说就前三个点来看，p【3】有可能是凸包上的点；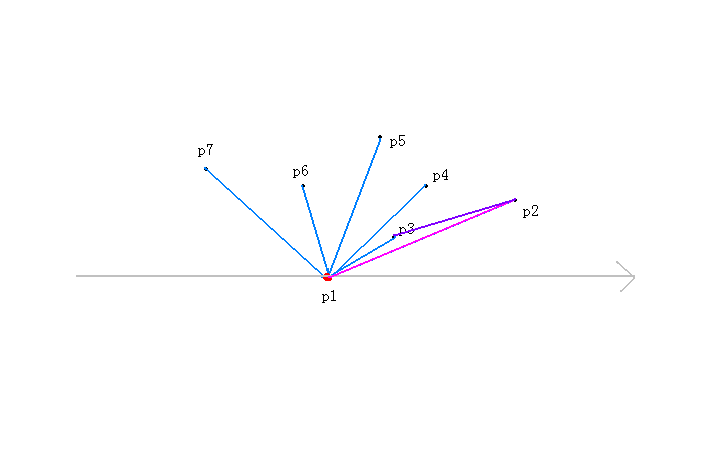

接着我们来看第四个点，进入while循环

1.对于p【top-1】也就是p【2】来说，p【top】也就是p【3】到p【4】为顺时针，所以multi小于0,执行top--操作，也就是说去掉了p【3】这个点；
2.接着继续看，对于p【top-1】也就是p【1】来说，p【top】也就是p【2】到p【4】为逆时针，所以multi大于0,不执行top--操作；

接着加入p【4】这个点。也就是说就前四个点来看，p【4】有可能是凸包上的点；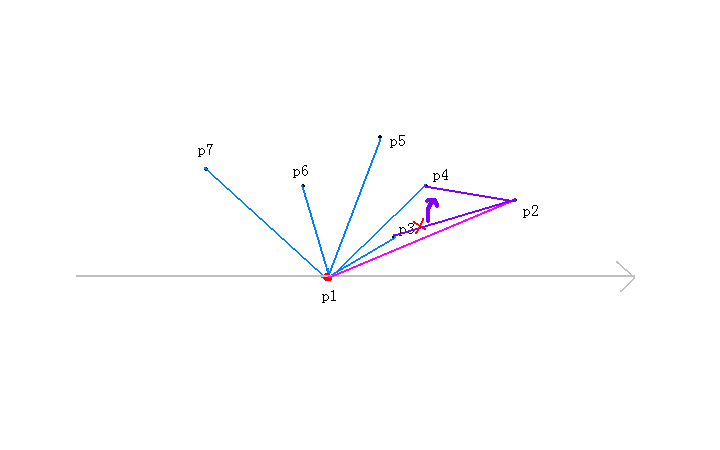

接着我们来看第五个点，进入while循环

1.对于p【top-1】也就是p【2】来说，p【top】也就是p【4】到p【5】为顺时针，所以multi小于0,执行top--操作，也就是说去掉了p【4】这个点；
2.接着继续看，对于p【top-1】也就是p【1】来说，p【top】也就是p【2】到p【5】为逆时针，所以multi大于0,不执行top--操作；

接着加入p【5】这个点。也就是说就前五个点来看，p【5】有可能是凸包上的点；

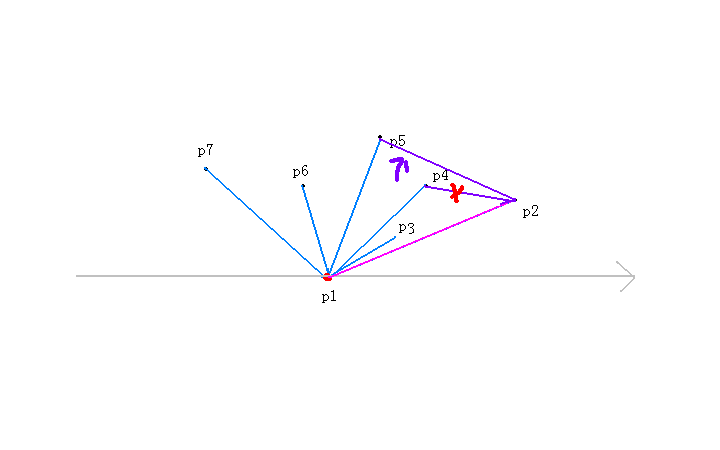
接着我们试着加入第六个点，进入while循环

我们对于p【top-1】也就是p【2】来说，p【top】也就是p【5】到p【6】为逆时针，所以multi大于0,不执行top--操作，

加入p【6】这个点。也就是说就前六个点来看，p【6】有可能是凸包上的点；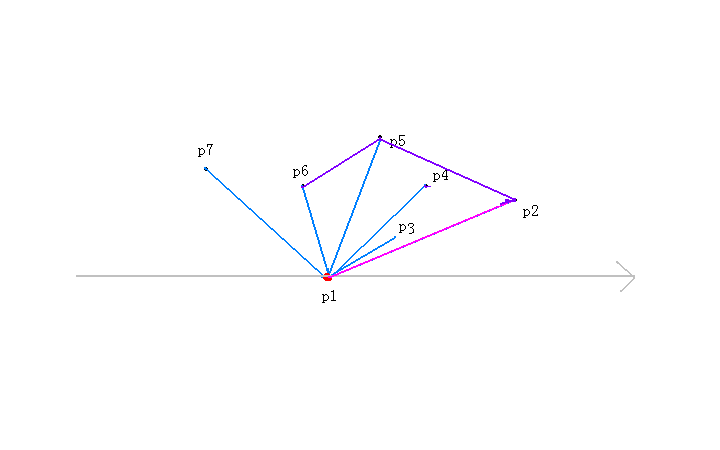

接着我们来看第七个点，进入while循环

1.对于p【top-1】也就是p【5】来说，p【top】也就是p【6】到p【7】为顺时针，所以multi小于0,执行top--操作，也就是说去掉了p【6】这个点；
2.接着继续看，对于p【top-1】也就是p【2】来说，p【top】也就是p【5】到p【7】为逆时针，所以multi大于0,不执行top--操作；

接着加入p【7】这个点。也就是说就前七个点来看，p【7】有可能是凸包上的点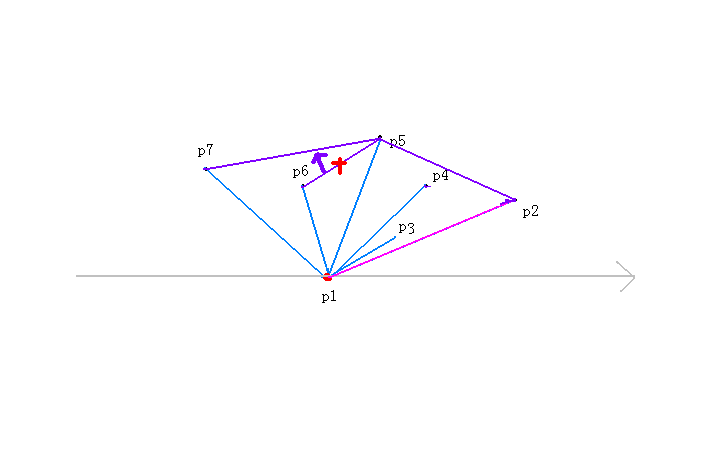

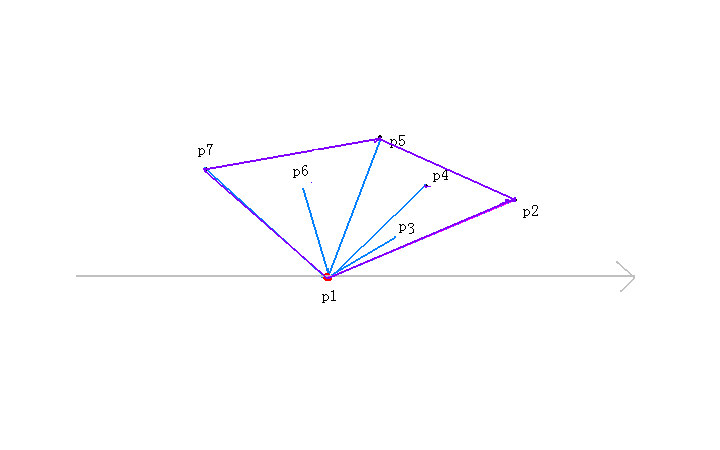
最后我们来看一号点p【1】，进入while循环

我们对于p【top-1】也就是p【5】来说，p【top】也就是p【7】到p【1】为逆时针，所以multi大于0,不执行top--操作，

加入一号点p【1】到sta，凸包完美的连成了一个闭合的图形！是不是很清晰明了呢？

为了方便起见，一般把一号点加到p数组末尾，但其实是不必要的，这是为什么呢？

如下图，当我们操作到原p数组最后一个点时，如果不判断，直接连接pn和p1（图中红色边），就有可能画出来的图形不是一个凸包，所以需要在队尾加上p【1】，在连接前把不合法的点退掉，看起来这样才能得到正确的答案！但是我们仔细想想，我们的每个点都是经过极角排序的，所以连接顺序不可能出现下图这个情况。

简单的模板题

【caioj 1214】凸包

时间限制: 1 Sec 内存限制: 128 MB
题目描述
【题意】
在一个平面坐标系上有n个点，用笔画一个多边形，使得多边形包含这n个点（点在多边形的边上也算包含）。
求多边形的最小周长。
【输入格式】
第一行整数 n (1 <= n <= 1000),表示有n个点。
下来n行，每行两个整数x（横坐标）和y（纵坐标），表示点坐标（-10000<=x,y<=10000)。
【输出格式】
一行一个实数，即多边形的最小周长（保留4位小数）。
【样例1输入】
4
2 1
5 1
5 5
2 5
【样例1输出】
14.0000
【样例2输入】
5
2 1
5 1
3 2
5 3
2 3
【样例2输出】
10.0000

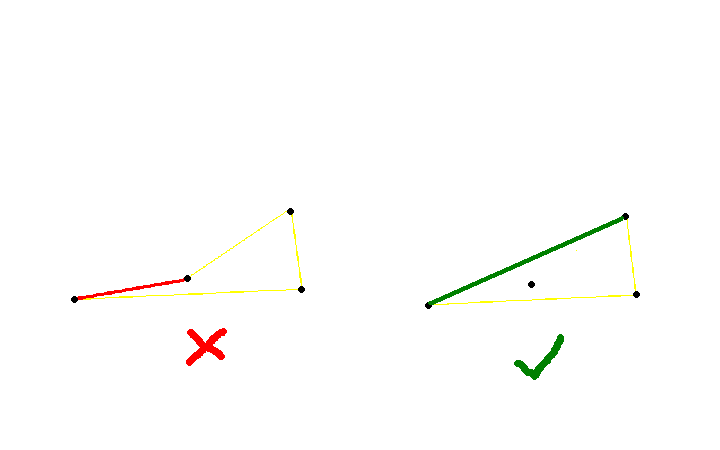
这道题要求的是一个能包围所有点的多边形，且周长最短，很明显，周长最短时就是这些点集的凸包【不知道为什么？看一下下图】

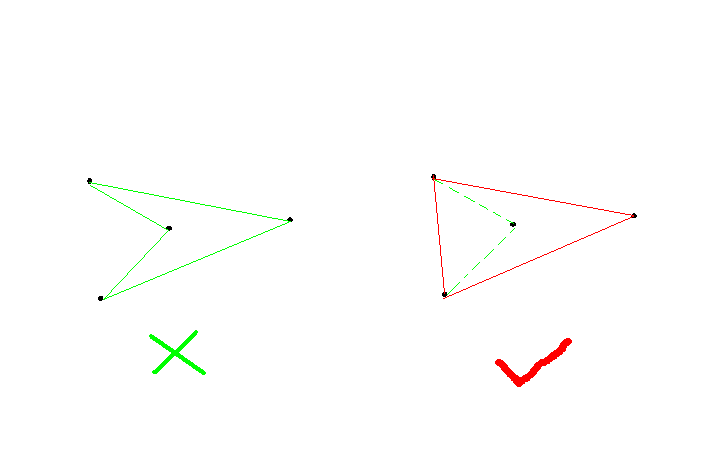
从图的右边可以很明显的看出，凸多边形的周长小于凹多边形（毕竟三角形中，两边之和大于第三边）。所以只要凸包求出凸包上的所有点，继而计算凸包的周长就行了。

附上模板（也是凸包模板）：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
struct node
{
    int x,y;
}p[11000],sta[11000];

int i,j,k,m,n,o,js,jl,top;
double ans;

double multi(node p1,node p2, node p0)
{
    double x1=p1.x-p0.x;
    double y1=p1.y-p0.y; 

    double x2=p2.x-p0.x;
    double y2=p2.y-p0.y;

    return(x1*y2-x2*y1); 
}//计算叉积 

double dis(node p1,node p2)
{
    return sqrt(double((p1.x-p2.x)*(p1.x-p2.x))+double((p1.y-p2.y)*(p1.y-p2.y)));
}//计算任意两点间距离 

bool cmp(node p1,node p2)
{
    int tt=multi(p1,p2,p[1]);
    if(tt<0)return(0);
    if(tt==0 && dis(p1,p[1])>dis(p2,p[1]))return(0);
    return(1);
}

void graham()
{
    sort(p+2,p+n+1,cmp);
    for(int i=1;i<=2;i++)sta[i]=p[i];
    top=2;
    n++;p[n]=p[1];

    for(int i=3;i<=n;i++)
    {
        while(top>1 && multi(sta[top],p[i],sta[top-1])<=0)top--;
        top++;
        sta[top]=p[i];

    }
}

int main()
{

    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",&p[i].x,&p[i].y);
        if(p[i].y<p[1].y ||(p[i].y==p[1].y && p[i].x<p[1].x))
        {
            node t=p[1];p[1]=p[i];p[i]=t;
        }//找最下方的点 
    }

    top=0;//记录凸包上点的个数 
    graham();
    double ans=0.0;
    for(int i=2;i<=top;i++)ans=ans+dis(sta[i],sta[i-1]);

    printf("%0.4lf",ans);

    return 0;
}

结语

上次本来说可能在计算几何的路上走不下去了，现在看来好像还能走一小段路啊__（接下来的貌似就难到飞起了）:smiley:希望这篇博客能帮助到你或者给你一点点启发！
最后给大家推荐一些题目：
练习：

pku1113 wall 赤裸裸的凸包问题，凸包周长加上圆周
pku2007 Scrambled Polygon 凸包，按极角序输出方案
pku1228 Grandpa's Estate爷爷的房地产 确定凸包的唯一性（就是每条土包边至少三个点以上），两个点的图形不算凸包。
pku3348 cows 求凸包的面积/50 的整数部分。用叉积求面积。
pku1873 The Fortified Forest 99年worldfinal的题。值得推荐的。枚举+凸包
pku1654 Area 刘汝佳的题！推荐。计算有向面积，要固定一个点。题目默认固定了（0，0）点(注意会超内存的，而且估算一下要用LL）
fzu1015 地主分地 判断线段相交+找点点规律
pku1269 Intersecting Lines 判断 直线相交并且求交点
pku2653 Pick-up sticks 判断线段相交