在比赛中，我们经常会遇到看到题目一时想不到正解的情况。这时我们要做的并不是放弃题目启动扫雷，而是应该先从部分分的思路想起。因为许多题目正解的解题思路，就隐藏在部分分的解决方法中。

从部分分到正解

解决一道题目时，依照不同的部分分写不同复杂度的算法是
很简单的，这只是一个经验问题。今天要讲的是如何根据部分分（特殊情况），找到突破口，进而解决全部问题。

一般来讲，典型的部分分（特殊情况）的转化有：“n, m” ->“n = m”、“树” -> “链”、“图” -> “ 树”、“ 动态” -> “ 静态”、
“在线” -> “离线” 等。

接下来就让我们从几道例题来深入体会这种解题技巧吧！

树上连续路径

题目描述

给出一棵 n 个点的树，问树上有多少条路径，满足编号的
范围是连续的。(1 ≤ n ≤ 3 × 105)

解题思路

直接考虑树上情况好像不好处理，所以我们先考虑如果是一条链怎么办：假设这条链上第 i 个点的编号是 a[i]，编号为 i 的点位于 b[i] 处，也就是说 a[b[i]] = i。

接下来我们考虑如何判断一段链上的一段区间[l,r]编号是否连续呢？我们有两种很显然的方法：

第一种方法我们可以统计链上[l,r]上的编号的最大值max和最小值min，如果max-min+1==lenth；那么[l，r]这一段的编号一定是连续的；但是貌似在程序中不太好操作，查询最值耗时也比较大，所以我们考虑另一种做法；

第二种做法我们可以设f(l,r) 表示 [l,r] 这段区间的长度减去这段区间中形如(i, i + 1) 这种点对的出现次数，那么当且仅当 f(l,r) = 0 时，[l,r]是一条合法的路径。

这时我们先假设我们求解出来了f数组，接下来我们只要建立一个二维坐标系，横轴表示 l，纵轴表示 r，(l,r) 处表示 f(l,r)。那么只需要统计这个坐标系中 1 ≤ l,r ≤ n 这 n^2 个点中有多少个 0 即可。

剩下的问题就是如何快熟计算f(l,r)了：对于 (ai
, ai+1) 这个点对，其会对满足 1 ≤ l ≤ i, i + 1 ≤ r ≤ n 的点的 f 值产生 1 的贡献，因为这些区间都包含了(ai, ai+1) 这个点对。

而对于 (i, i + 1) 这个点对，其会对所有满足1 ≤ l ≤ min(bi, bi+1), max(bi, bi+1) ≤ r ≤ n 的点的 f 值产生 −1 的贡献，如下图所示：

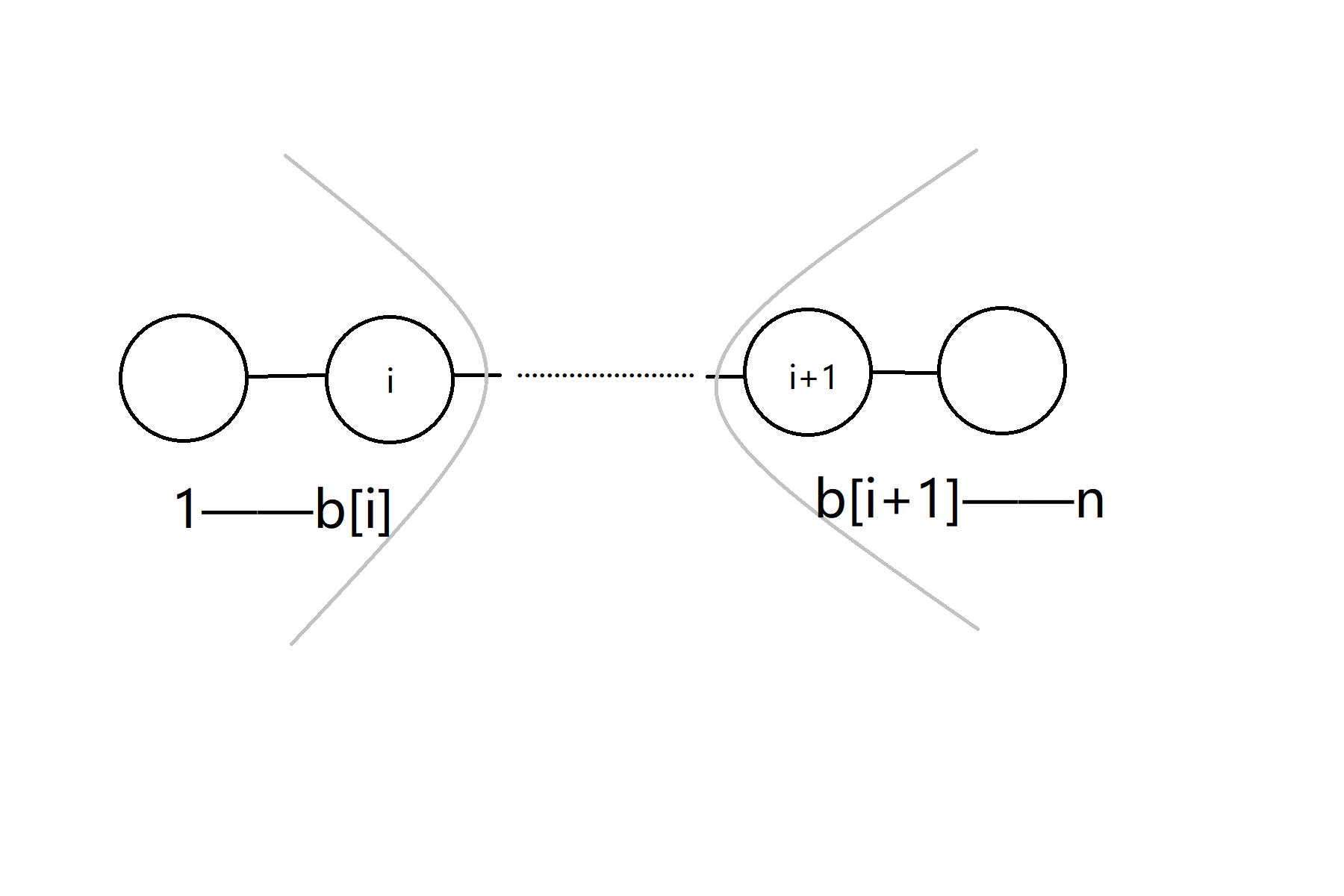
这些贡献都是一块矩形区域，扫描线 + 线段树维护即可。
时间复杂度 O(n log n)。具体为什么是一个矩阵呢？比如上图我们x从[1,b[i]]y从[b[i+1],n]都要减一，我们要操作的区间就如下图所示：

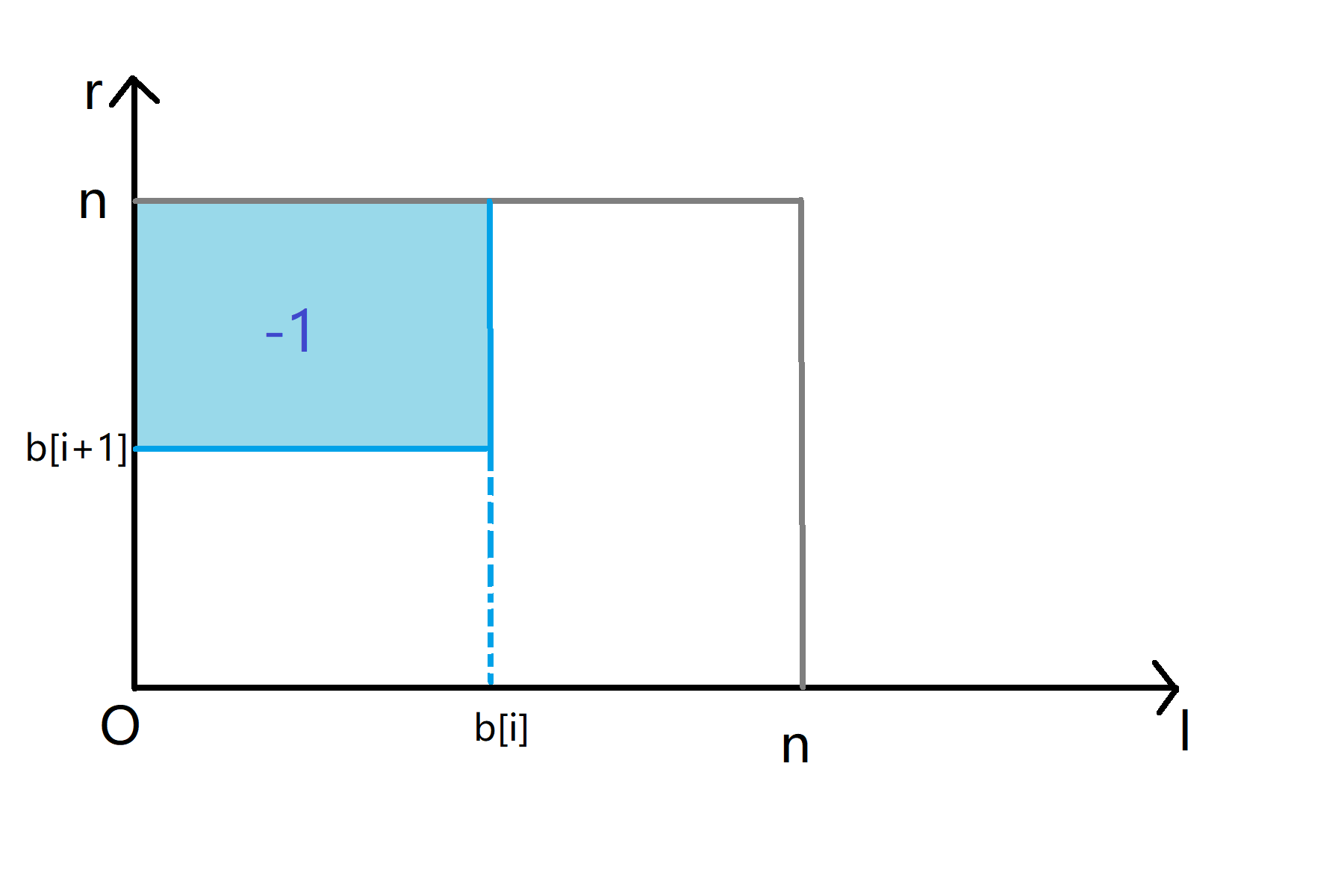
这样这道题链的情况就做完了。但是你肯定不满足与此，于是你开始考虑上述做法如何推广到树上？

首先很显然的一个结论，就是树上任意一颗子树内所有点的DFS序是连续的。所以问题就很简单了。我们先在树上跑出每个点的DFS序，接着我们考虑如何想上面链的情况一样处理每一条边的权值。我们先考虑对于一条边 (u, v)，不妨设 v 是 u 的父亲，那么其会一个端点在 u 的子树内，一个端点在 v 的子树外（包括 v）的所有路径产生 1 的贡献。然后又由于是对子树的贡献，容易发现如果用 dfs 序来表示，贡献也是若干个矩形。正如下图，我们设整棵树一共有n个节点，以i为根节点的一个子树中根节点i的DFS序为dfn[i]，这颗子树中DFS序最大的点DFS序为low[i],那么如下图：

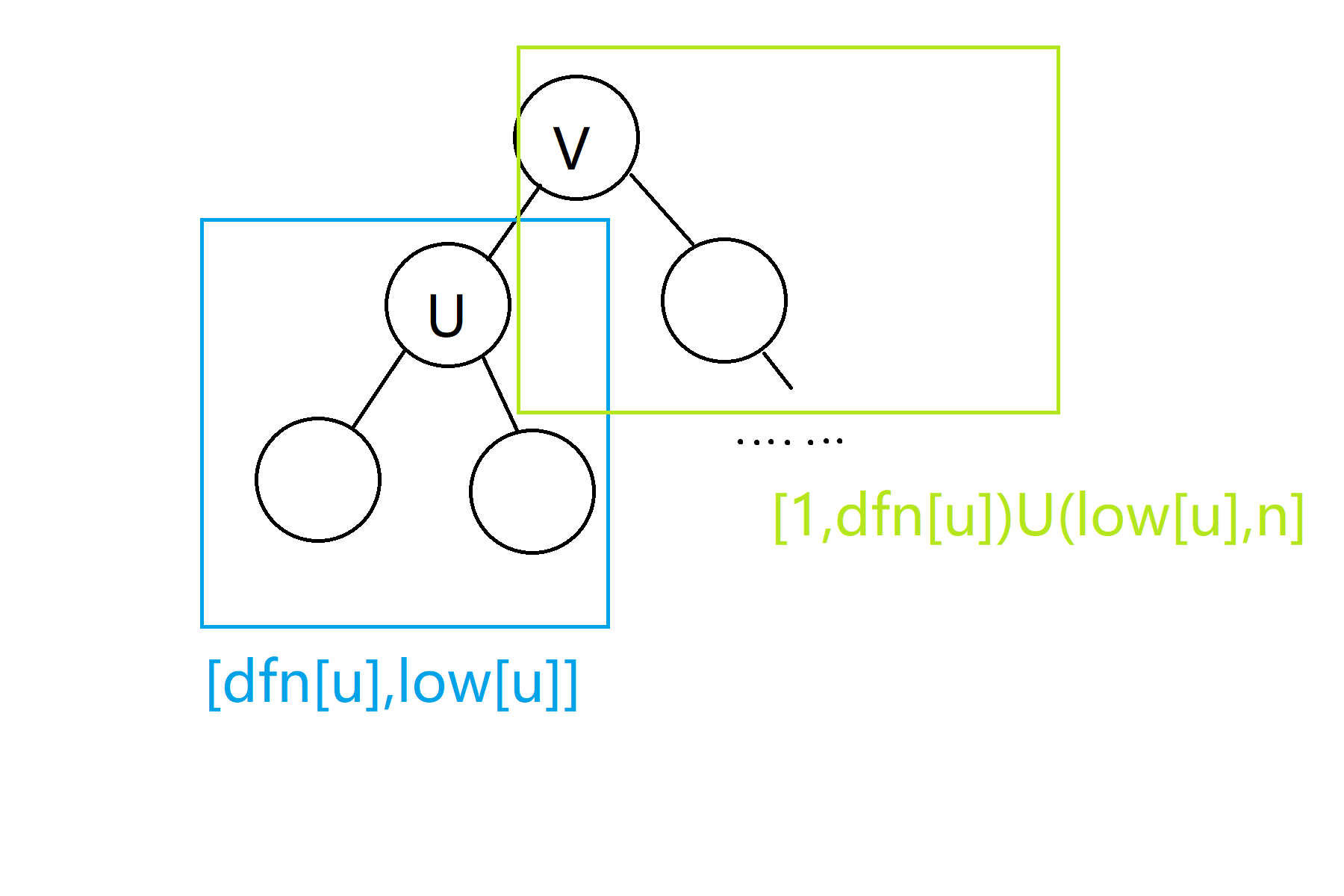
接着对于一个点对 (i, i + 1)，经过讨论也可以发现贡献也和上面所述的情况类似，是 dfs序上的矩形，所以一样的操作就可以啦。

所以总的来说树上的维护和链上维护方式相同，时间复杂度 O(n log n)

Alice 和 Bob

题目描述

Alice 和 Bob 在玩游戏，开始时有 n 堆石子，第 i 堆石子有 ai 个，Alice 和 Bob 轮流取石子。Alice 每次必须从一堆石子内恰好取 x 个，Bob 每次必须从一堆石子内恰好取 y 个。谁不能取了谁输，Alice 先手，两人都以最优策略取，问谁会赢。
1 ≤ n ≤ 10^5。
1 ≤ ai , x, y ≤ 10^9。

解题思路

首先，乍一看这道题，貌似确实没有想到什么特别好的思路，所以我们首先先考虑一下最特殊的情况——x=y；

x=y

对于第 i 堆石子，可以被取 [ai/x] 次。所有石子可以被取 ∑[ai/x] 次，只需要判断这个数的奇偶性即可。

接着我们发现在x=y的时候，对于任意一堆石子不论是加上2kx个石子，还是减去2kx个石子，答案的奇偶性都不会改变，答案也不会发生改变；

更进一步，我们发现对于一堆石子 ai，其加上 k(x + y) 或减去 k(x + y) 都不影响答案，即如果 ai = ai mod (x + y)，答案不变。

经过归纳发现这个结论在 n != m 时也成立。接下来我们考虑一下普通的情况：

x<y

由于 ai 对 x + y 取模后答案不变，所以将 ai 对 x + y 取模，那么 0 ≤ ai < x + y，即：一堆石子至多只能被一个人取。又因为 ai < x 的石子没有贡献，不妨删掉，所以有 x ≤ ai < x + y。

接下来我们又分两种情况进行讨论：

如果存在一个 i，使得 x ≤ ai < y，那么先手必胜。因为先手总可以优先取 ai ≥ y 的堆直到取完，这时他还有石子可以取，而后手已经没有可以取的石子了。

如果不存在这样的堆，那么所有堆都有 ai ≥ y。此时如果存在一堆满足 ai ≥ 2x，那么先手必胜。因为先手可以开场取这堆，从而构造出一堆满足 x ≤ ai < y 的石子。否则每堆石子都只能恰好被取一次，判断石子堆数的奇偶性即可。

x>y

情况和上面类似：

一样的由于 ai 对 x + y 取模后答案不变，所以将 ai 对 x + y 取模，那么 0 ≤ ai < x + y，同样有一堆石子至多只能被一个人取。又因为 ai < y 的石子没有贡献，不妨删掉，所以有 y ≤ ai < x + y。

接下来我们同样又分两种情况进行讨论：

我们发现，如果存在一个 i，使得 y ≤ ai < x，那么后手一定必胜吗?不一定，在这种情况下，只有两种可能后手能取胜，一个是存在另一个j，使得 y ≤ aj < x；或者此时能产生贡献的石子的堆数为偶数；

同样的，在第二种大情况下，如果不存在y ≤ ai < x的堆，那么所有堆都有 ai ≥ x。此时如果存在两堆满足 ai ≥ 2y，那么后手必胜。因为先手足够聪明，一定会开场取一堆这样的堆，只有后手再取一堆这样的堆，从而构造出一堆满足 x ≤ ai < y 的石子。否则每堆石子都只能恰好被取一次，判断石子堆数的奇偶性即可。

到这里这道题就做完啦。

卡片机器

题目描述

初始时你有一张卡片 (a, b) 以及三台机器，这三台机器的功能分别如下：
投入一张 (x, y)，生成一张 (x + 1, y + 1)。
投入一张 (x, y)，生成一张 (x / 2 ,y / 2)。需保证 x, y 均为偶数。
投入一张 (x, y) 和 (y, z)，生成一张 (x, z)。
注意：机器工作完成后会将投入的卡片返还。
现在你希望得到卡片 (c, d)，问是否能在 10000 步内达成，
如果能，输出方案，否则输出 −1。
1 ≤ a, b, c, d ≤ 1000。

解题思路

这道题看到的第一眼——完了没思路怎么办。不要慌张，我们可以先从最特殊的情况入手——a = b；

首先考虑 a = b 的情况：
容易发现如果 a = b，生成的所有卡片也是两数相等的。又因为显然可以用前两台机器将 (a, b) 变为 (1, 1)，(1, 1)又能变成任意(x, x),所以只要c = d，就一定可以。否则一定不行。

接下来考虑 a < b 的情况：
容易发现如果 a < b，生成的所有卡片也是第一个数小于第二个数的。我们可以使用前两台机器把 (a, b) 变为相差最小的两个数，即 (1, x)，其中 x 是偶数,因为如果 x 为奇数，则(1,x)--(2,1+x)--(1,(1+x)/2),又 x 大于 1 ，所以(1,(1+x)/2) 差会小于 (1, x) 的差，是更优的。那么 x − 1 是两数之差可能的最小值。也就是说如果d − c < x − 1，那一定无解。

如果有解，则显然需要满足 (x − 1)|(d − c)。假设
d − c = k(x − 1)，接下来只需要考虑如何将 (1, x) 变为(1, k(x − 1) + 1)。

其实很简单，先用前两部机器由 (1, x) 得到 (1, k(x − 1) + 1) 的策略如下：
先由 (1, x) 得到 (x, 2x − 1),(2x − 1, 3x − 2), · · · ,((k − 1)(x − 1) + 1, k(x − 1) + 1)，再由机器三得到 (1, 2x−1),(1, 3x−2), · · · ,(1, k(x−1) + 1) 即可。

接着a > b 的情况只需要交换 a, b 和 c, d 即可。所以这道题就做完啦。

循环的网格

题目描述

一个 n × m 的网格，你可以给每个格子填一个方向（右或
下），要求从左上角开始沿着给出的方向走，可以将所有格子恰好经过一次且返回起点。问有多少种定向方法。
网格是循环的，也就是说如果某一步走出了网格，你会到网格的另一边。（2 ≤ n, m ≤ 10^5）

解题思路

首先我们注意到，每个格子都的方向都只能是向下或向右，所以我们观察到到如果 (i, j) 处往右走，那么 (i, j + 1) 是从 (i, j) 过来的，也就意味着 (i − 1, j + 1) 处不能往下走，所以 (i − 1, j + 1) 也要往右走。同理往下走也一样。所以可以得到：网格的次对角线上的格子的方向一定相同。即对于每一个格子，他填的方向与他右上方的格子填的方向是一样的。

考虑 gcd(n, m) = 1 的情况，此时从任意一点出发，不断向右上方走，可以走遍所有点，就如下图。即所有点的方向必须一样，这是显然不可以的，所以无解，所以gcd(n, m) ≠ 1。

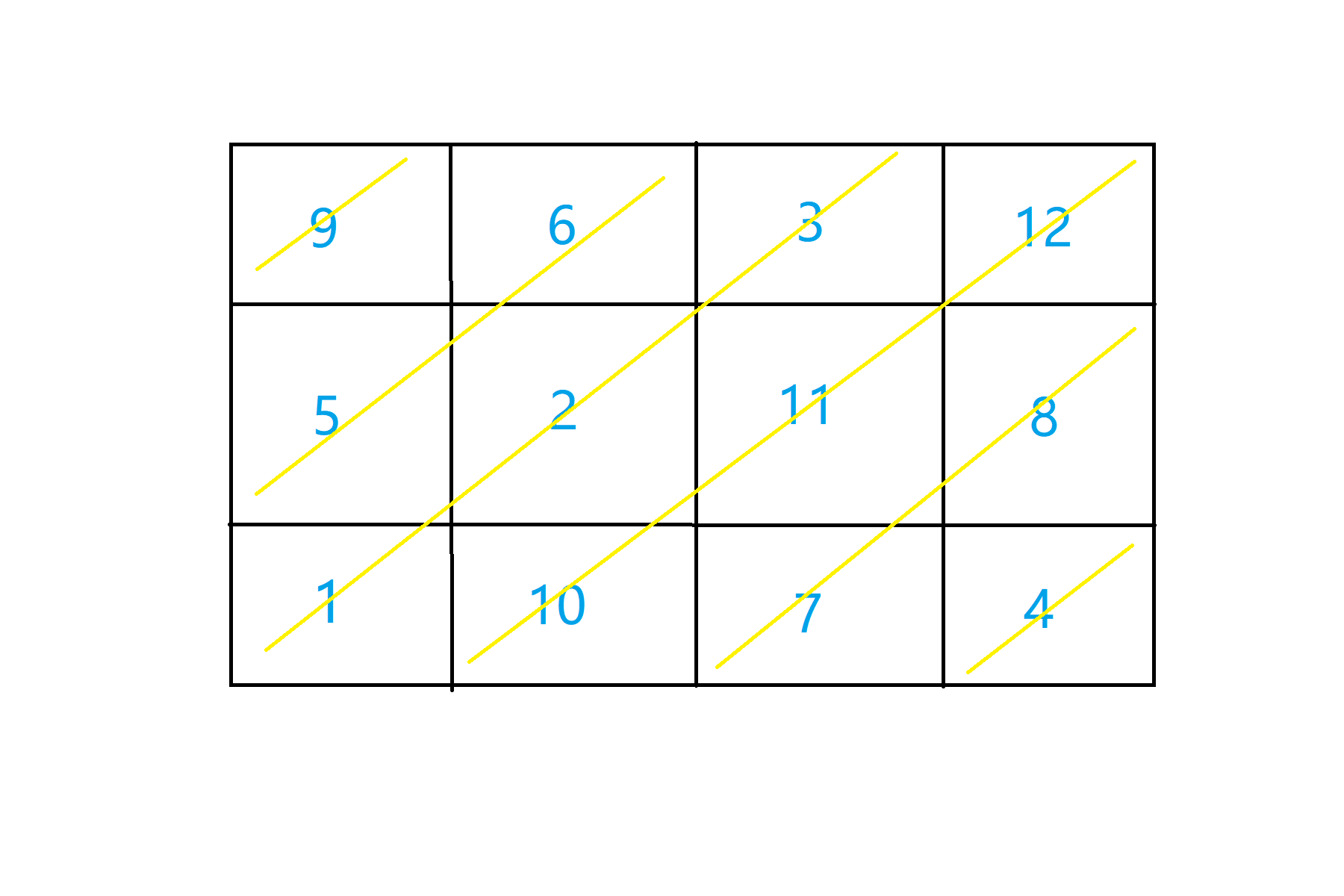
接下来考虑 n = m 的情况，此时恰好有 n 条次对角线，现在需要给这 n 条次对角线分配向右还是向下。

设这 n 条次对角线中有 i 个是向右走的，n − i 个向下走的。那么走 n^2 步之后会走到 (ni mod n, n(n − i) mod n) = (0, 0)，即无论怎么分配，走 n^2 步之后都会返回起点。

但是只保证走 n^2 步后返回起点还不够，要保证这 n^2 步经过的点都是不相同的。考虑从起点走 kn 步后会到哪里，因为 kn步经过了 k 轮次对角线，所以往右走了 ki 步，往下走了 k(n − i)步，即到了 (ki mod n, k(n − i) mod n) 这个点。我们需要保证当 k < n 时，这个点都不为 (0, 0)。

即问多少个 i 满足 ki mod n = 0, k(n - i) mod n = 0 当1 < k < n 时都不成立。显然当且仅当 gcd(i, n) = 1 时满足。所以枚举往右走的步数 i，只有 gcd(i, n) = 1 时有贡献，贡献为 n!/[i!(n-i)!]。故答案为：

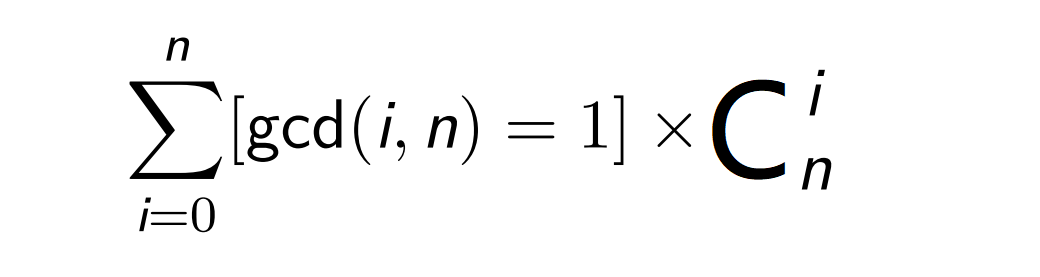
接下来考虑 n ̸= m 的情况，根据之前讨论，如果有解那么gcd(n, m) = g ̸= 1。画图后发现此时的网格共有 g 条次对角线，和 n = m 时使用相同的办法，可以发现当且仅gcd(i, n) = 1, gcd(g -i, m) = 1 时对答案有贡献，贡献为g!/[i!*(g-i)!]。所以答案为：

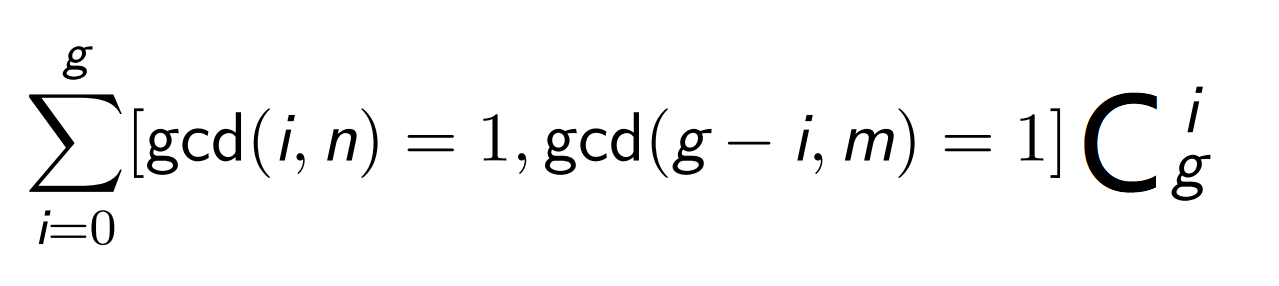
所以这道题就解决了！(听说NOI2018的冠军zzq6分钟就AC了这道题QwQ)

乌鸦抓松鼠

题目描述

给出一个 n 个点的树，开始时树上有两只乌鸦和一只松鼠，位于不同位置。现在要进行若干论操作，每轮操作将分为三步：
1、你选择一个乌鸦飞到天上。
2、松鼠在树上随机移动，但不能经过另一只乌鸦。
3、在天上的乌鸦降落回树上（落的位置在第一步确定）。
如果某次降落后，乌鸦恰好在松鼠所在位置，那么松鼠被抓住。问如何操作乌鸦，使得在最坏情况下抓住松鼠的步数最少。（2 ≤ n ≤ 10^5）

解题思路

在树上可能比较难思考，我们首先考虑一条链的情况：一种策略是两只乌鸦借助边界一步一步卡松鼠的活动范围：

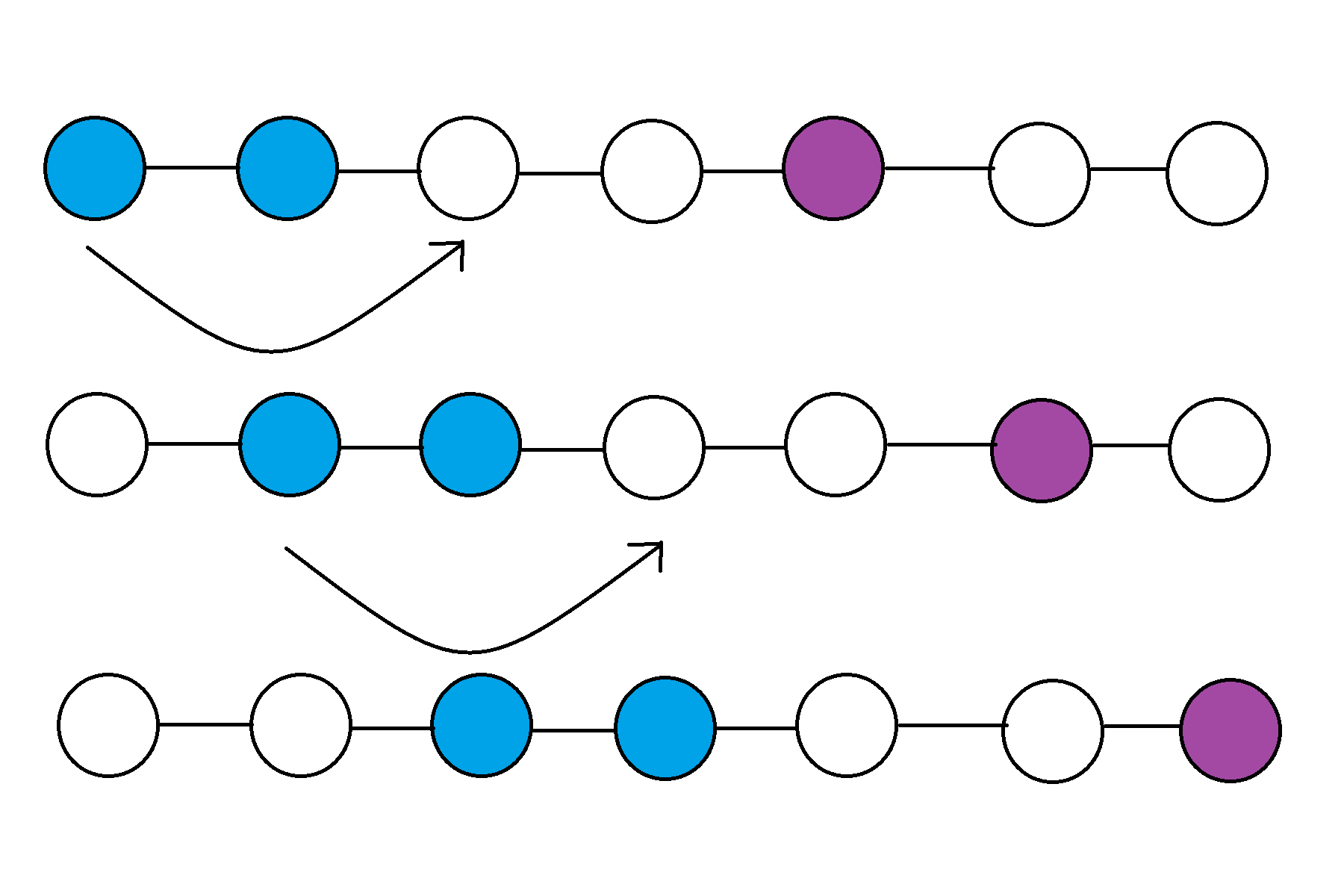
还有一种策略是某只乌鸦先到某一点，使得松鼠的活动范围减小，之后两只乌鸦再借助边界卡松鼠：

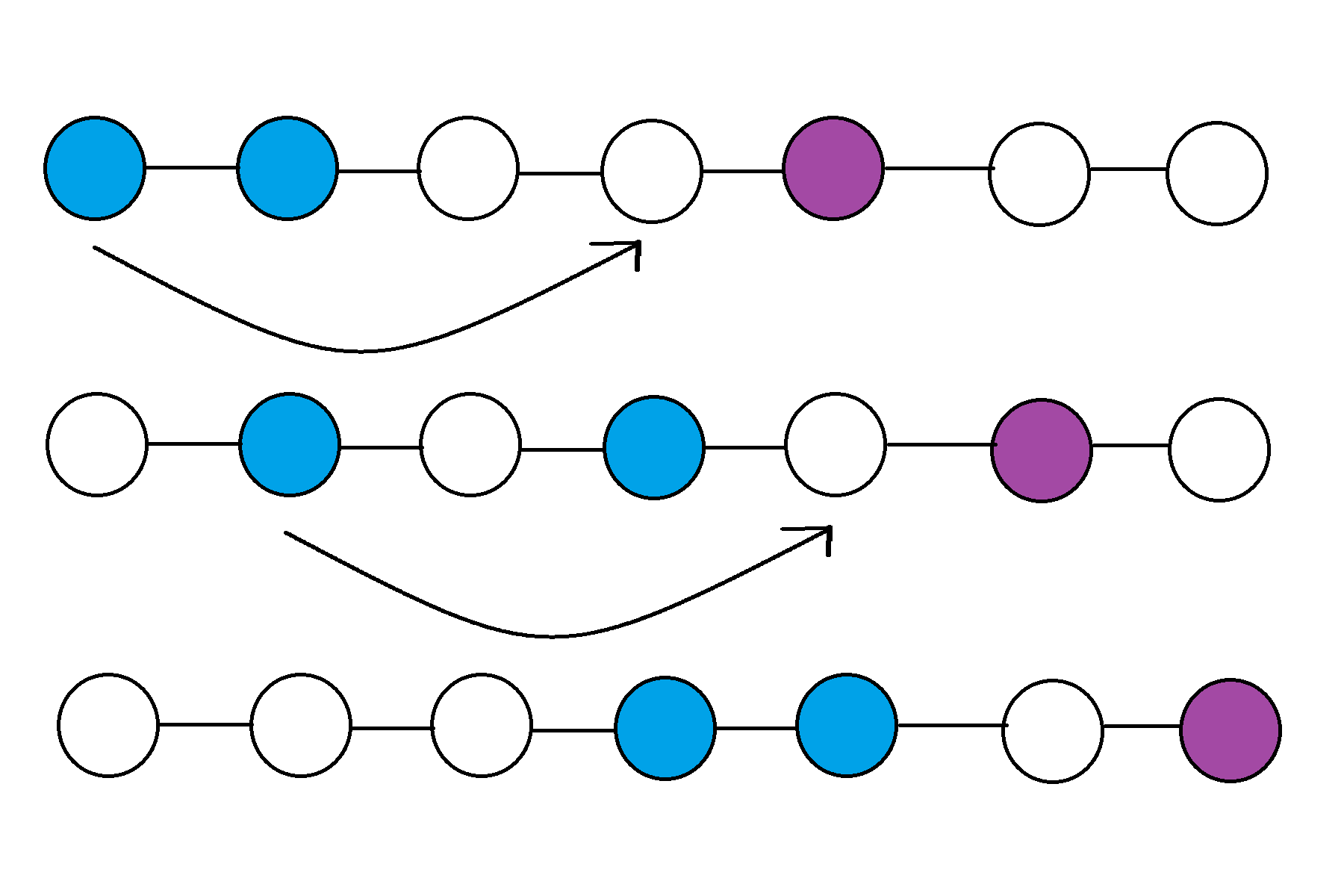
树上也是如此：
一种情况是以某只乌鸦为根，之后两只乌鸦轮流将松鼠往子树中卡，此时答案就是根的松鼠方向的儿子的子树的最大深度。

另一种情况是某只乌鸦先跳到某个点上，并以该点为根，接下来同上一种情况。对于第二种情况，需要枚举第一步前往的所有点，所以复杂度 O(n^2)。当然这个复杂度是过不了的，我们考虑一下优化。

注意到第二种情况的答案就是：

也即：

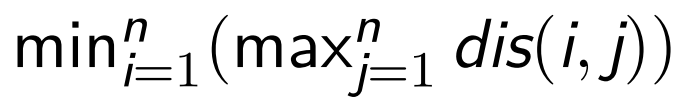
显然这个数为直径除以二上取整。时间复杂度 O(n)。

添加符号

题目描述

给出 n 个数，在这 n 个数的 n-1 个间隔中加入加号或乘号，问对于所有的 2^(n-1) 种情况，所有表达式的值的和为多少。答案模 10^9 + 7。
同时你还要支持 q 次修改操作：每次给你两个数 p b，表示把 p 处的值修改为 b，输出修改后的答案。1 ≤ n, q ≤ 10^5。

解题思路

首先不考虑修改操作：
用一个二元组 (ai, bi) 来表示一个表达式的值，含义为这个表达式最后一个加号前的结果为 ai，最后一个加号之后的数的乘积为 bi。那么如果在这个表达式后面加入一个数 c，将会产生两个新表达式 (ai + bi, c) 和 (ai, bi × c)。设当前一共有 n 个二元组，那么加入一个 c 之后，将变成2n 个二元组。

这么写有上面好处呢？我们设我们当前有n个表达式，我们看下图：

我们发现，设之前所有二元组的和为 (A,B)，那么加入一个 c 之后，将变成 (2A + B, c(n + B))。所以只要扫一遍并维护 A, B, n 即可。时间复杂度 O(n)。

考虑转移 (A,B, n) → (2A + B, c(n + B), 2n)。写成矩阵形式：

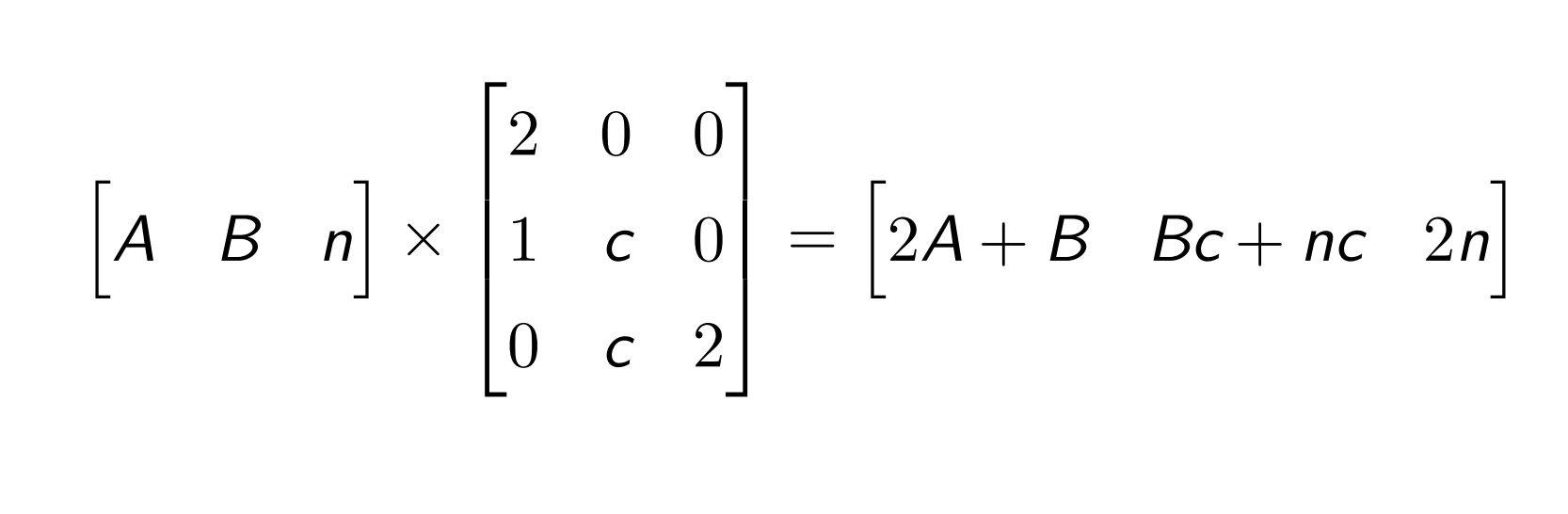
所以答案即为若干个矩阵的连乘，修改 c 即修改某个位置的矩阵。线段树维护即可，时间复杂度 O(n log n)。

最后再介绍一下线段树如何维护矩阵吧，我们每个叶子节点都是一个关于c的矩阵，第i个c要改变，就修改第i个叶子节点的矩阵，每个父亲节点代表的是其两个儿子节点的矩阵乘积，所以根节点就是我们的答案了，如下图：

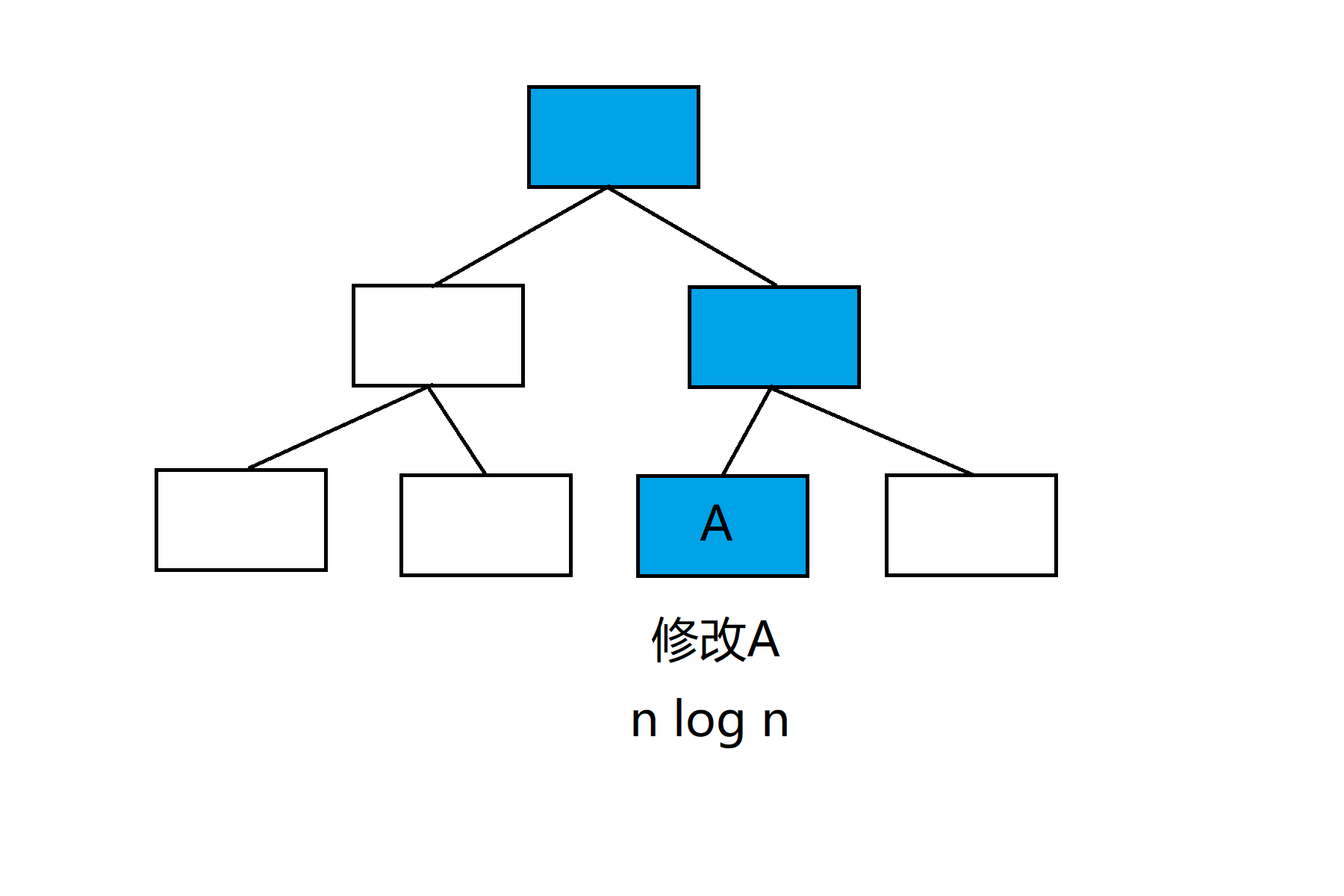
到这里这道题就结束啦。

结语

这篇BLOG我们介绍了一种很重要的思想——从特殊到一般，这是在众多学科中都适用的规律，最后希望你能掌握这项技能，也希望你能喜欢这篇BLOG!