在接下来的两篇BLOG中，我们将要学习一种新的无监督学习模型——推荐系统(recommender systems)，这也是我们日常生活中见到的最多的机器学习算法之一了，下面就让我们一起来看看吧！

推荐系统

我们在这个阶段学习推荐系统有两方面的动机，第一个原因就是它是机器学习的一个重要应用，过去的几年中推荐学习系统一直是硅谷的各种科技类公司所重点关注和运用的机器学习算法，在当今社会可以带来极大的经济收益；第二个原因是，对于机器学习来说特征量的选择对于算法而言是异常重要的，而一些推荐系统算法就能试图自动地替你学习到一组优良的特征量，可以应用到更多机器学习的算法上。

那说了这么多就让我们正式开始吧。我们先看看推荐系统问题是怎么样的。举个例子，预测电影评分这个时兴的问题大家应该都知道吧， 就是假想我们有的一个，销售或出租电影的网站，我们让用户使用0至5颗星给不同的电影评分，比如像下图这样：

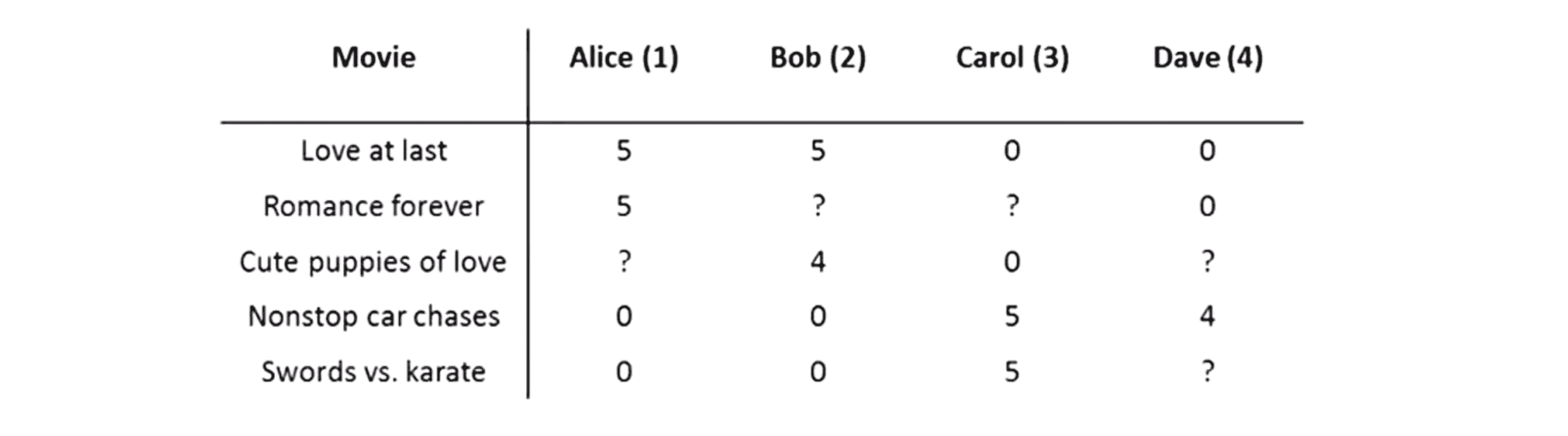
在这个例子中，我们有5部电影分别是 《爱到最后》 《浪漫永远》 《小爱犬》 《无尽狂飙》 还有 《剑与空手道》，我们有还4位用户 名叫 Alice Bob Carol 和 Dave 首字母为A B C和D。那些？代表的是用户没有评分的电影。为了更好地说明，我们在这里再引入一些符号：

我们将用 nu 表示用户数量，在这个例子中 nu = 4；我们用 nm 来表示电影数量，比如这里我有5部电影，于是 nm = 5；接着我们有数值 r(i, j) 表示如果用户 i 给电影 j 评过分，那么 r(i, j) = 1，反之等于 0；最后我们还有数值 y(i, j) 表示用户 j 给电影 i 的评分，当r(i, j) = 1时， y(i, j) 就会是一个 0 至 5 的数。

我们的推荐系统问题就是给定这些数据，然后我们能否通过浏览全部数据来预测这些带问号的地方应该是什么数值。为了解决这个问题，我们需要开发一个推荐系统算法，其主要工作就是通过学习已经填好的值，帮我们自动地填上这些缺失的数值。这样我们就能看一下用户还没看过哪些电影，然后向用户推荐新电影并试图预测还有什么电影可能会让这一位用户感兴趣。

这些就是推荐系统问题的正式表述，在下一部分，我们将开始开发一种学习算法来解决这个问题。

推荐系统算法

为了更方便地介绍推荐系统算法，我们还是用回刚刚的例子：假如我们有一些电影还有一些观众，他们每个人都对某些电影进行了一些评价打分我们想做的是通过这些用户的评价来预测出他们会怎样给还没看过的电影打分：

在这一部分中，我们将学习一种简单好用的推荐系统的方法，这种方法叫做“基于内容的推荐系统算法”。上图是我们之前的数据集，其nu = 4，代表有四名用户；nm = 5代表有五部电影，那么我应该如何预测这些缺少的值呢？

我们假设对这些电影的每一部我都用一些特征来描述，具体来说我们假设每部电影有两种特征分别用x1和x2代表，其中x1表示这部电影属于爱情电影的程度，x2表示这部电影属于动作电影的程度，然后我们得到了如下数据：

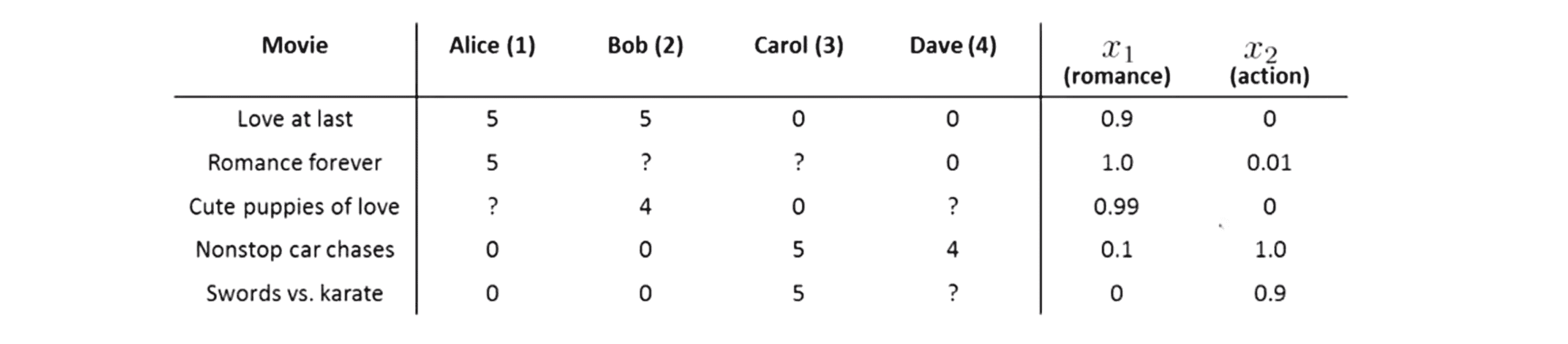
所以对于每部电影我们的特征都可以用一个特征向量来表示，比如对于第一部电影《爱到最后》 ，其特征向量就是[0.9, 0]，前后两个元素分别是 x1 和 x2。为了方便后续计算，我们还是像以前一样加一个额外的特征变量——截距特征变量 x0 其值恒为 1，把三个特征变量放在一起这样我就有了特征 x(1)：[1, 0.9, 0]。所以特征 x(1) 就是电影《爱到最后》的特征向量，对电影《浪漫永远》 我们有另外一个特征向量 x(2)等等以此类推最后电影《剑与空手道》 有另外一个向量 x(5)。

为了进行预测，我们可以这么做：我们可以把对每个观众打分的预测当成一个独立的线性回归问题。具体来说比如对于每一个用户 j ，我们都学习出一个参数 θ(j) 代表其对不同类型电影的喜好程度。在这里是 θ(j) 一个三维向量，更一般的情况是 θ(j) 为一个 n + 1 维向量，其中 n 是电影不包括截距项 x0 的特征数量。然后我们要根据参数向量θ 与特征 x(i) 的内积来预测用户 j 对电影i的评分。

我们来看一个具体的例子吧，现在假如我们想预测 Alice对电影 《小爱犬》 是如何评价的，那么这部电影有一个参数向量x(3) = [1 0.99 0]，其中1是截距项然后是两个特征 0.99和 0。假如说对于这个例子我们已经知道Alice的参数向量 θ(1) = [0 5 0] ，那么我们对这一项的预测 等于θ(1)^T * x(3) = 5 × 0.99 = 4.95,因此我对这个值的预测 其结果将为 4.95。这看起来算是一个比较合理的预测。而如果我们像预测所以的四个用户对第一部电影《爱到最后》的评分，我们也可以按如下步骤计算：

因此我们做的事情实际上就是对每个用户应用不同的线性回归模型，并得到每个用户分别对应的 θ 向量。写成如下更正式一些的形式，我们用r(i,j) = 1 来表示用户 j 对电影 i 进行了评分，y(i,j)则表示用户 j 对电影 i 的评分值。如果这个用户 j 对这部电影 i 没有进行过评价，那么我们就估计这个用户对这部电影的评分就为θ(j)^T * x(i)：

为了方便求解 θ ，我们需要临时引入一个表示符号 m(j)，我们用 m(j) 来表示用户j评价过的电影的数量。那具体为了学习参数向量 θ(j) 我们应该怎么做呢？这是一个基本的线性回归问题，我们要做的就是选择一个参数向量θ(j) 使得预测的结果与真实结果尽可能接近。即为了求解 θ(j) ，我们要将下面这个代价函数最小化：

即我们对那些 r(i,j) = 1 时的所有i（第 i 部电影），对所有用户 j 所评价过的电影的估计值（θ(j)^T * x(i)）与真实值（y(i,j)）相减再平方得到的平方误差进行累加，再加上我们的正则化项就得到了我们的代价函数。记得我们之前的代价函数前后两项的系数都是1/2m，这次我们同时乘上m系数变成1/2m其实代表的都是一样的意思。同样地需要注意的地方，再这里的正则化求和是从k等于1到n，我们仍然不需要对x0进行正则化。因此如果我们对这个式子关于θ(j)求最小值的话，就会得到一个很好的 θ(j) 的估计值来预测出用户 j 对电影的评分值。

当然在构建推荐系统的时候，我们也不想只对某一个用户学习出参数向量，我们想对所有的用户都学习出 θ。因为我有nu 个用户，所以我们希望一次性学习出所有的参数。我们要做的是将 nu 个代价函数累加再调整一下系数就得到了下面这个代价函数：

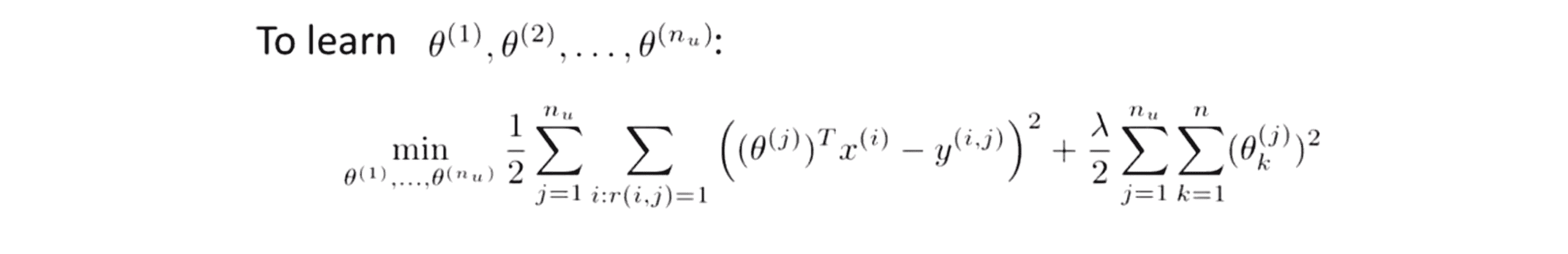
所以这里的表达式前面是1/2 这实际上就跟我们上面的一样，唯一不同的是现在不是只对一个 θ(j) 进行优化，现在我们要同时对所有的用户求这个目标函数的和进行优化求求最小值。当我这个式子关于θ(1) θ(2) 一直到 θ(nu) 最小化时，我们就会得到对每个用户不同的参数向量，然后我可以用它们来对所有的用户来作出预测了。

我们来总结一下方法，下图中最上面的就是我们的最优化目标，给这个项起一个名字吧，就叫它J(θ(1), ... ,θ(n_u))吧。同样地 J 还是我们要最小化的最优化目标函数。接下来为了求出这个最小值，我们可以使用梯度下降法来进行更新迭代，而在梯度下降中，我们需要求出代价函数的偏导数，其就如下图中下面这样， 每次更新我们就用 θ(j)k 减去学习速率 α 乘以右边这一项：

对于 k = 0 和 k ≠ 0 的情况，我们的式子有一点点区别。因为我们的正则化项只对 k 不为 0 的θ(j)k 进行正则化，因此我们不对 θ0 进行正则化。因此这实际上就是我们之前就熟悉的梯度下降法。

当然用这些微分项，如果你愿意的话，你也可以把它们用在 更高级的优化算法里，比如聚类下降或者L-BFGS(Limited-memory Broyden–Fletcher–Goldfarb–Shanno Algorithm) 或者别的方法来最小化代价函数 J。这就是我们基于内容的推荐系统算法的全部内容了。

结语

通过这篇BLOG，相信你应该知道了怎样应用基于内容的推荐系统算法来对未知的内容进行预测。但事实上对很多电影我们并没有这些特征，或者说我们很难得到所有电影的特征，或者很难知道我们要卖的产品有什么样的特征。所以在下一篇BLOG中，我们将谈到一种不基于内容的推荐系统来处理特征信息。最后希望你喜欢这篇BLOG！