我们之所以选择Octave作为我们机器学习的实现语言，其中还有一个很重要的原因就是Octave自带方便快捷的图像库，可以输出大量图像来为我们检测算法带来事半功倍的效果。下面就让我们一同来看看如何在Octave中实现图像的绘制吧。

为何要图像绘制

当开发学习算法的时候，往往几个简单的图就可以可以让我们更好地理解算法的内容，并且可以完整地检查算法是否正常运行。例如在之前BLOG中，我们提到了绘制代价函数J(θ) 可以帮助我们确认梯度下降算法是否收敛。

通常情况下绘制图像也同样会启发我们如何改进自己的学习算法。而Octave有非常方便的工具用来绘制大量，不同的图像。前辈的经验告诉我们，绘制数据、绘制学习算法往往是获得想法、改进算法的重要步骤。下面就让我们一同学习如何使用Octave的工具来绘制和可视化我们的数据。

函数图像绘制

在绘制函数图像前，我们要设置定义域t，其本质是一个均匀的数列，比如从0到0.98的集合：

接着让我们设置函数y1 = sin(2 * pi * 4 * t)（此处pi表示π）,而 y1 代表的就是一个定义域在[0, 0.98]的正弦函数。那我们如何绘制它呢？我只需要输入plot(t, y1);就出现了我们想要的图像：

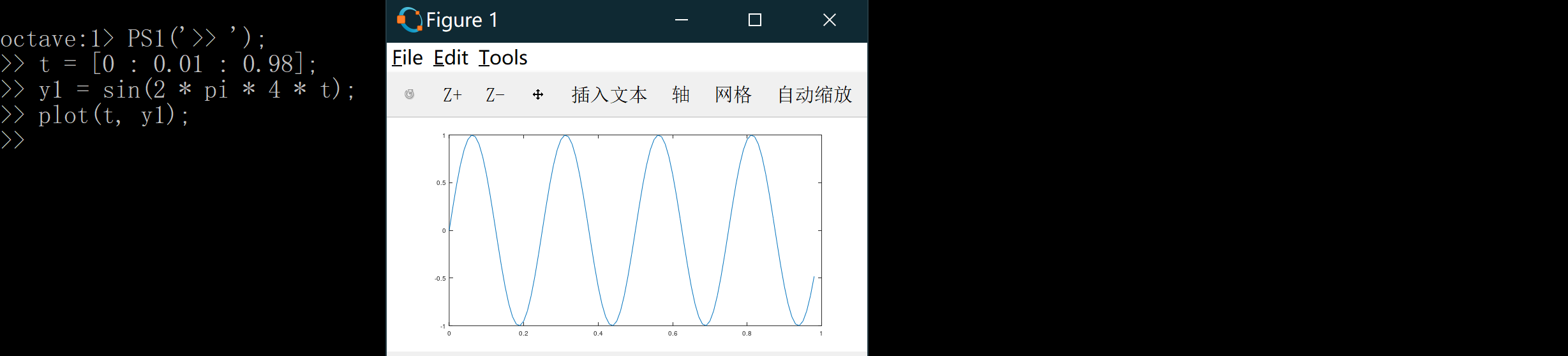
其中横轴是自变量 t ，纵轴是因变量 y1，也就是我们刚刚所输出的正弦函数。

让我们设置y2 = (cos 2 * pi * 4 * t) ,而如果我输入plot(t, y2);,Octave将会消除之前的正弦图,并且用这个余弦图来代替它:

如果你想要同时出现正弦图像和余弦图像，我们就可以我使用hold on;函数，其功能就是将新的图像绘制在旧的之上；同时我们可以用不同颜色绘制余弦函数plot(t, y2, 'r');:

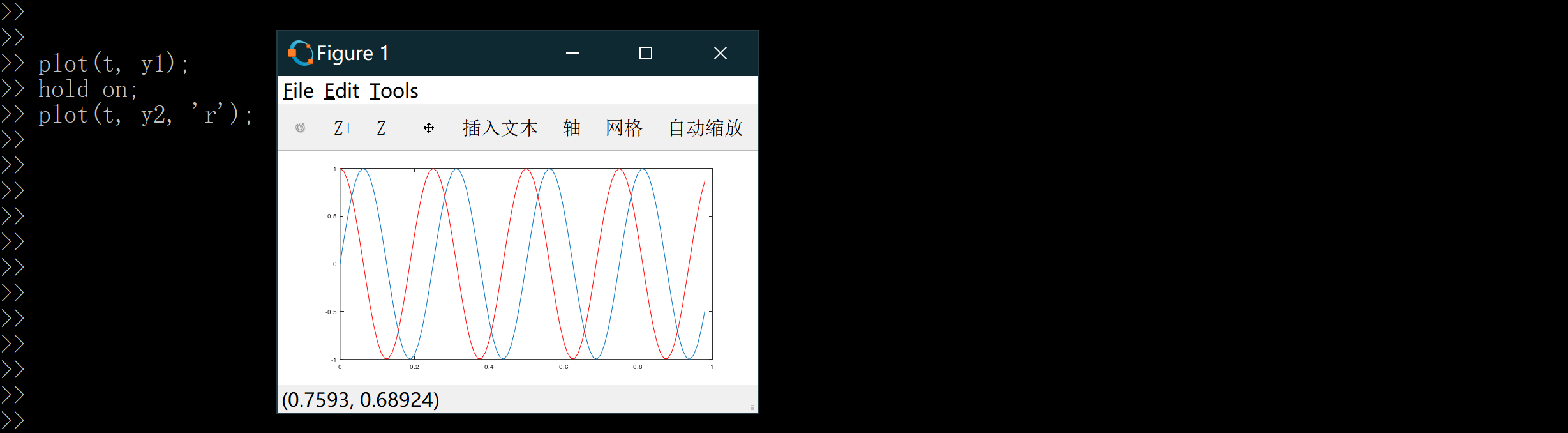
接下来我们可以使用命令xlabel('time'); 来标记X轴即水平轴的名字，用命令ylabel('value'); 来标记垂直轴的名字;同时我也可以用命令legend('sin', 'cos');来标记我的两条函数曲线,最后我们可以用命令title('myplot')在图像的顶部显示这幅图的标题：

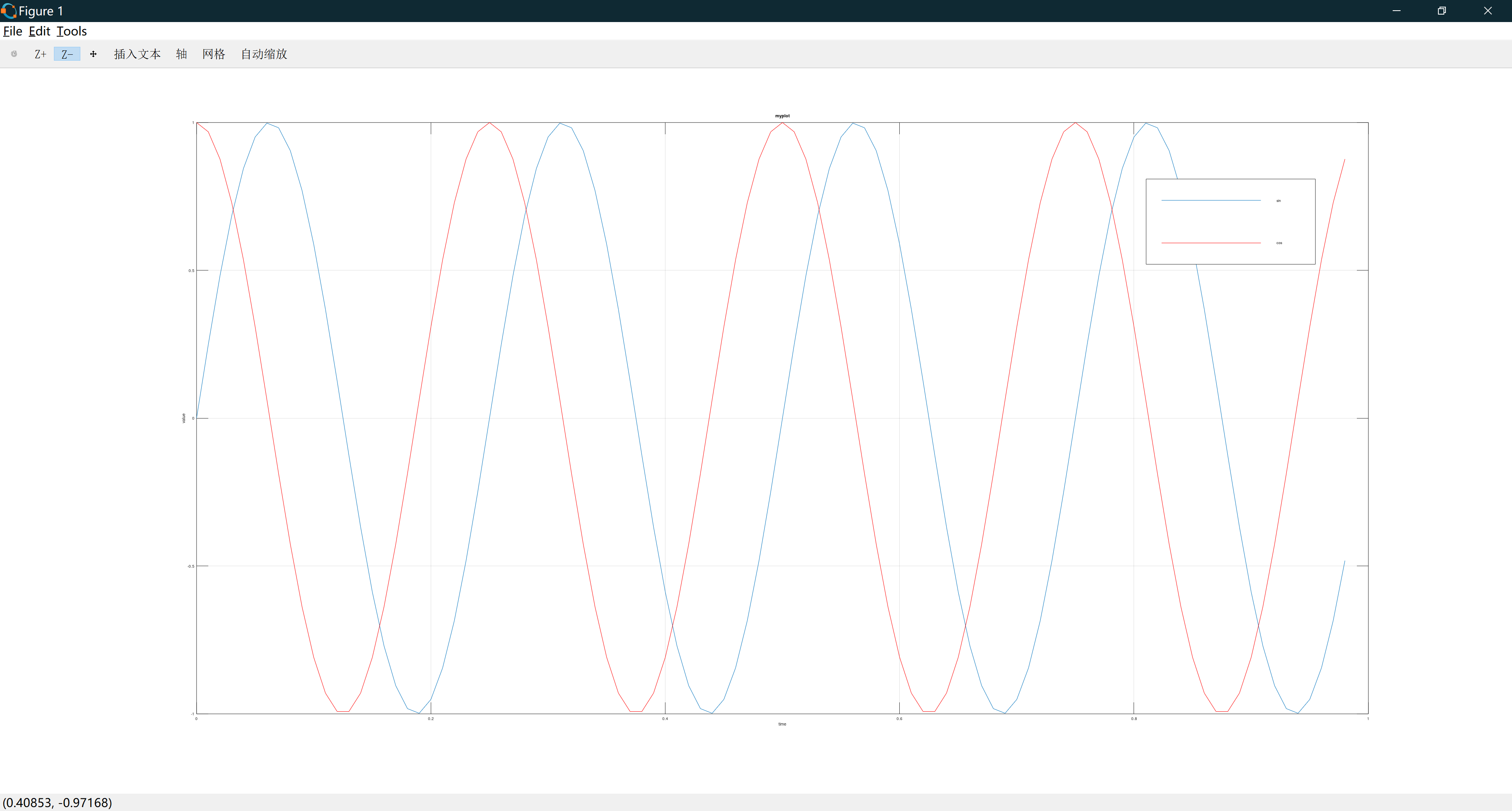
Octave也可以让你为图像标号，如果输入figure(1); plot(t, y1); 其将在第一个窗口显示第一张图，如果你想绘制第二个图，你可以指定一个不同的数字编号，比如输入figure(2); plot(t, y2); 其将在第二个窗口显示第二张图，正如这样：

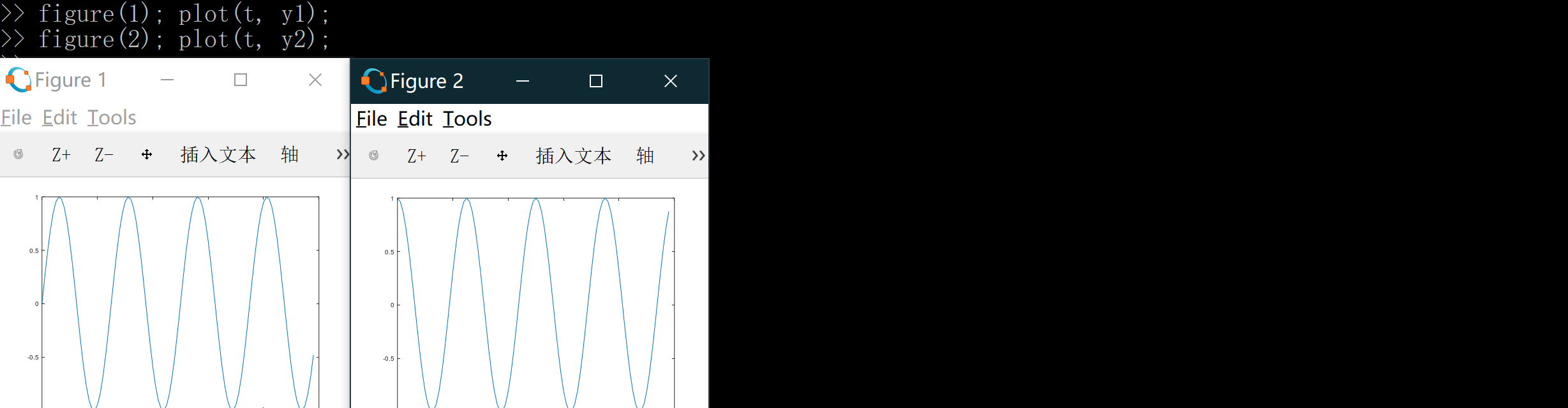
再经常介绍一个经常使用的命令-subplot()命令,如果我们想让两幅图分开显示在同一个窗口中，我们可以先使用subplot(1,2,1);将图像窗口分为一个 1*2 的区域，并且准备使用左边的区域:

然后我们使用命令subplot(1,2,1);plot(t, y1);就让 第一幅图显示在左边的区域，而如果我输入subplot(1,2,2);plot(t, y2); 就让第二幅图显示在右边的区域：

再介绍一个命令axis()，其改变轴的刻度，比如axis([0.5 1 -1 1])就是让横轴的范围调整至0.5到1 纵轴的范围为 -1 到 1：

最后再介绍一下命令 clf，其可以清除一幅图像：

顺带一提最后如果你想关闭这个图像窗口，你可以使用命令close来让这个图像窗口关掉。

矩阵图像绘制

Octave不仅可以输出函数图像，还可以用色块来输出矩阵。比如我们设置 A 是一个 5 × 5 的奇幻方阵，我们可以用一个巧妙的方法来可视化矩阵，也就是命令imagesc(A)，它将会绘制一个 5 * 5 的彩色格图矩阵，不同的颜色对应 A 矩阵中的不同值：

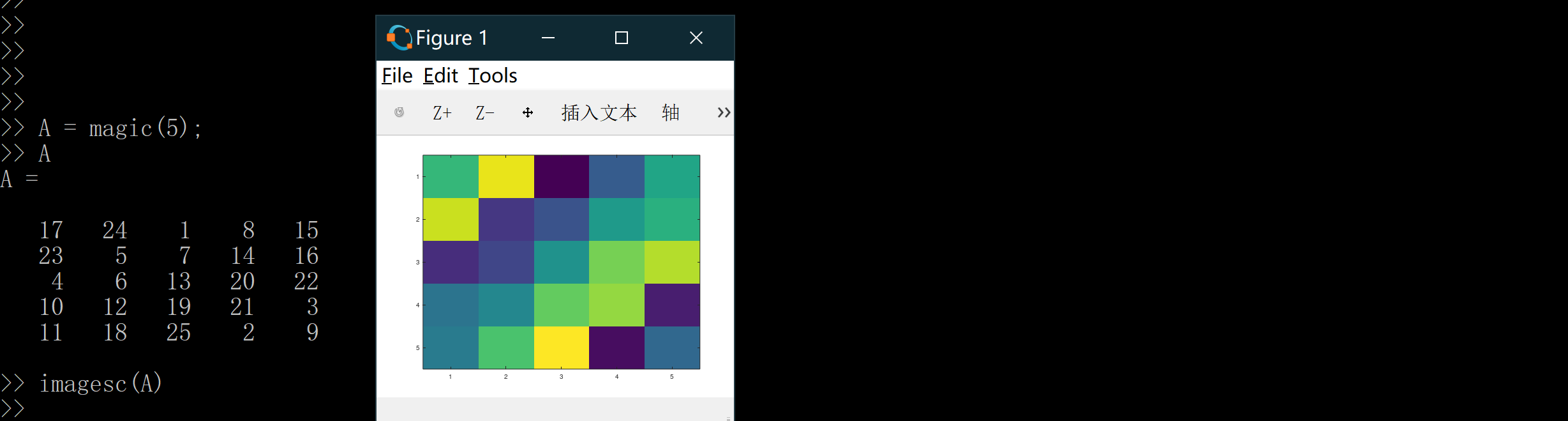
为了看得更清楚，我们可以使用一个更加复杂的命令 imagesc(A), colorbar, colormap gray; 这实际上是在同一时间运行三个命令,然后它生成了一个灰度分布图，并在右边也加入一个颜色条以显示不同深浅的颜色所对应的值：

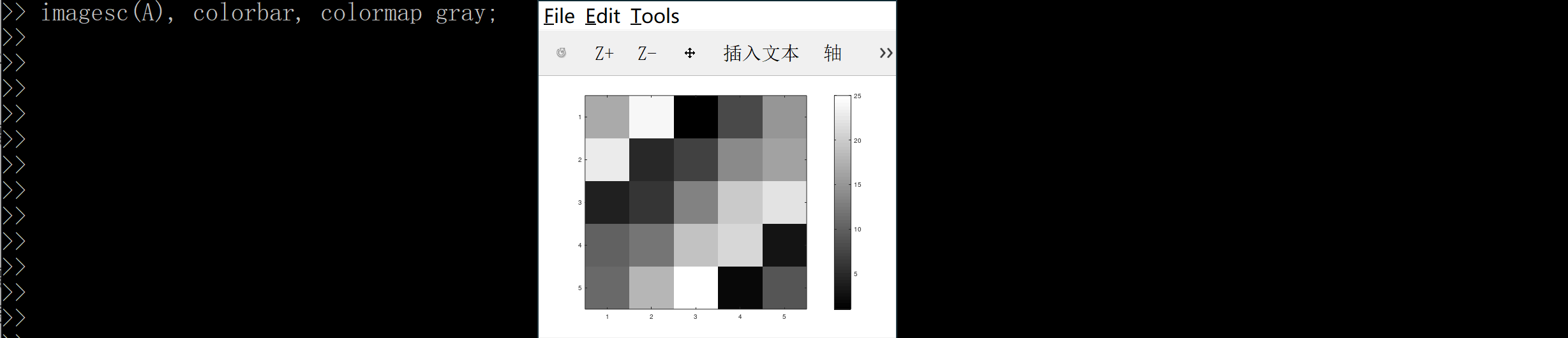
这里再举一个例子，我可以绘制一个更大的矩阵，比如imagesc(magic(15)), colorbar, colormap gray;我们将会得到一幅 15*15的magic方阵值的图：

图像输出保存

如果你想保存一幅图像，你只需要输入print -dpng 'myplot.png';就可以得到一个png图像文件：

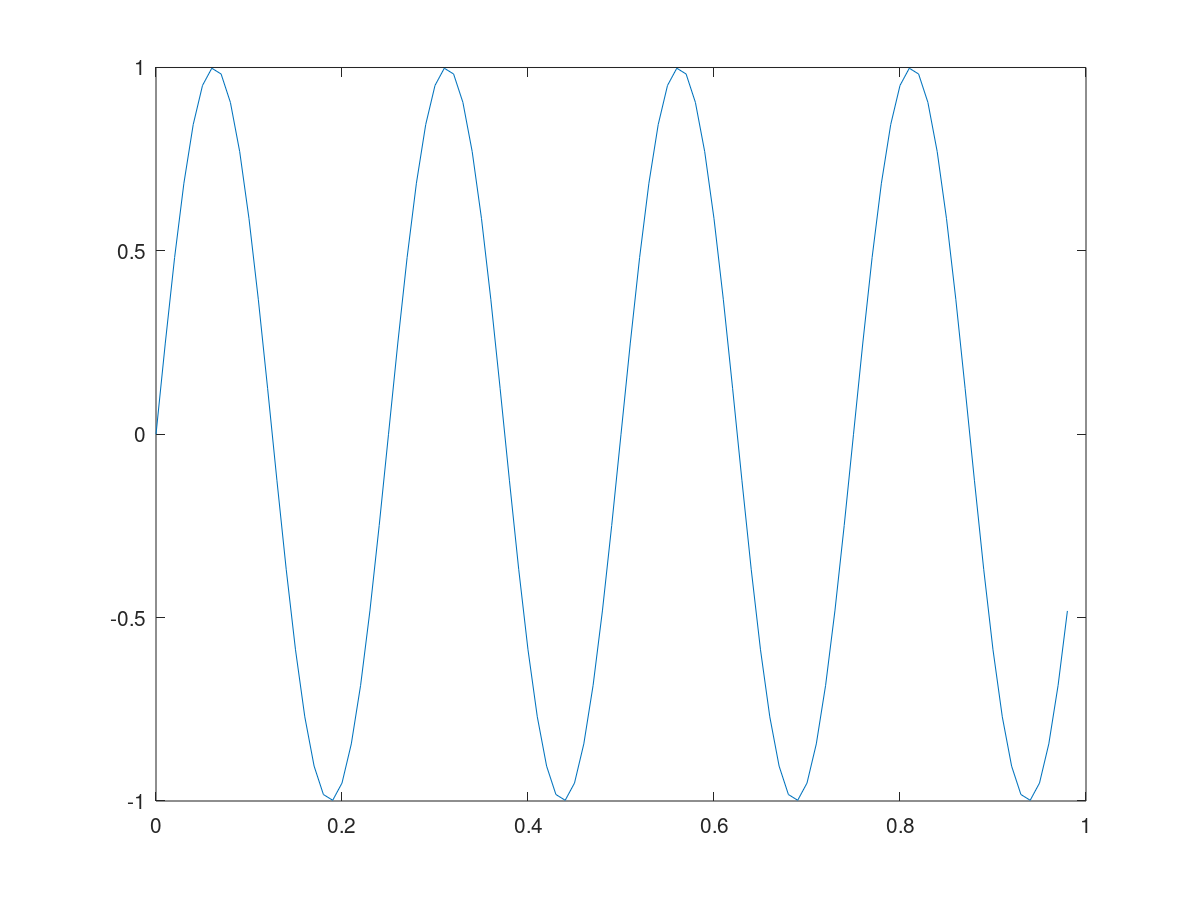
Octave也可以保存为很多其他的格式，你可以使用help print来查看更多。

结语

通过这篇BLOG，相信你已经知道如何绘制 Octave中绘制多种图像，接下来我们将回归语法讲讲Octave中的控制结构。最后希望你喜欢这篇BLOG！