在之前的BLOG里，我们通过例子讲解了神经网络的作用。现在让我们来看看如何定义我的代价函数已经如何最小化我们的代价函数吧。

代价函数

神经网络是当今最流行的学习算法之一，现在就让我们一同学习在给定训练集下为神经网络拟合参数的学习算法。正如我们之前学习的大多数学习算法一样，我们还是从拟合神经网络参数的代价函数开始讲起。

我们还是从例子入手。下图是神经网络结构，假设我们有一个像下面这样的训练集，其中有 m 个训练样本x(i) y(i)：

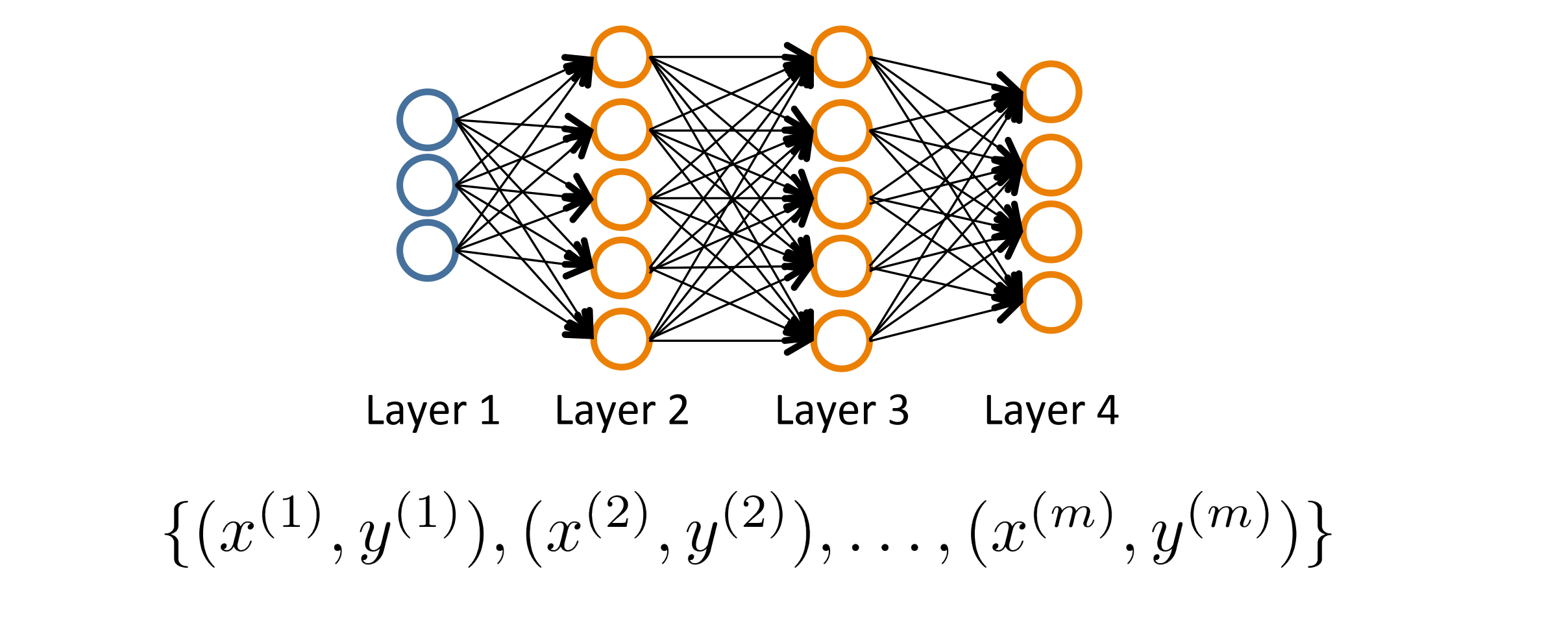
下面我们先来规定一些记号方式。我们用大写字母 L 来表示这个神经网络结构的总层数。所以对于上图的网络结构，我们有 L = 4。然后我用 si 表示第 i 层的单元的数量，也就是神经元的数量，这其中不包括第 i 层的偏差单元。比如上图中，我们知道 s1 也就是输入层有 3 个单元，所以 s1 = 3；s2 在这个例子里等于5个单位……

我们一般情况下会讨论两种分类问题，第一种是二元分类，在这里y只能等于 0 或 1 ，一般只有一个输出单元，即 sL = 1。在这类问题里为了简化记法，我们通常我会记 K 为 1 ，即输出层的单元数目。第二种是多类别的分类问题。也就是会有多个不同的分类，在这类问题里，如果我们一共有 K 个范雷，那我们就会有K个输出单元。所以我们的假设函数输出的是一个K维向量。

现在我们来为神经网络定义代价函数。由于我们使用神经网络是来解决分类问题，所以我们在神经网络里使用的代价函数也应该是逻辑回归里使用的代价函数的一般化形式，即：

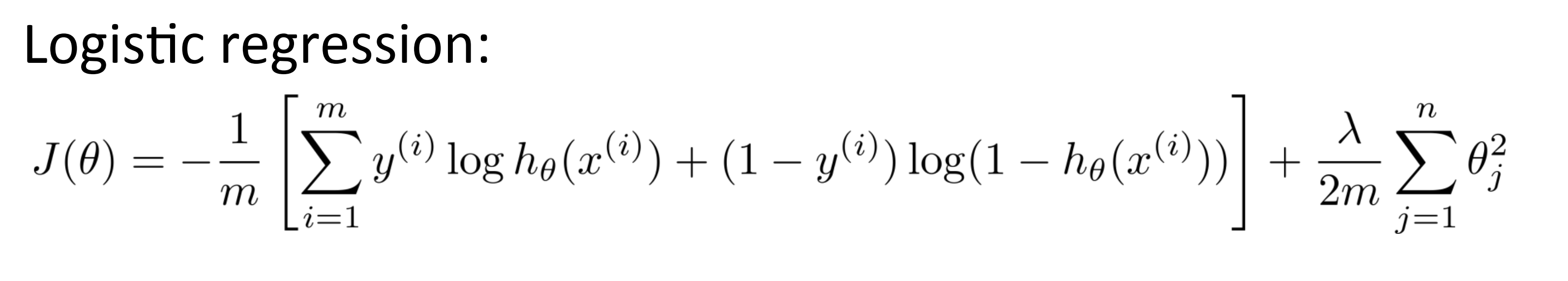
对于逻辑回归而言我们通常使代价函数 J(θ) 最小化，而对于一个神经网络来说，我们的代价函数是这个式子的一般化形式：

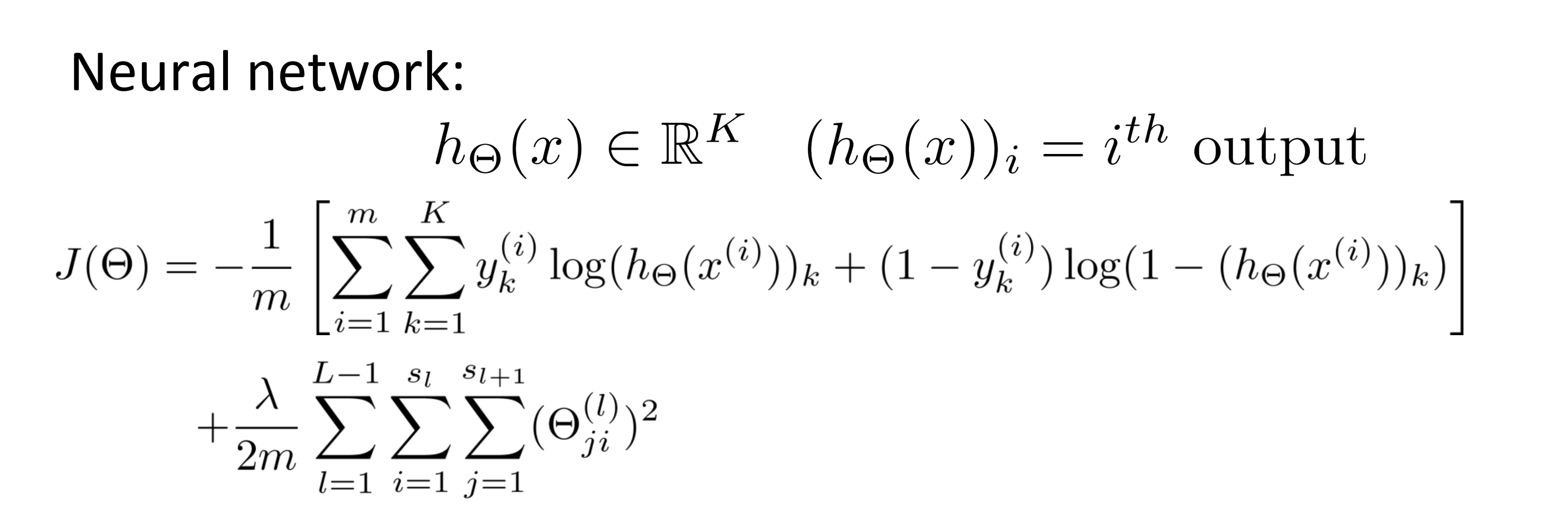
这里不再是仅有一个逻辑回归输出单元，取而代之的是 K 个。所以这是我们神经网络最后会输出一个 K 维的向量。这里 K 可以取到 1 ，其解决的就是原来的二元分类问题。我们用 h(x)i 来表示第i个输出。也就是说 h(x) 是一个 K 维向量， h(x)i 表示选择了神经网络输出向量的第 i 个元素。我的代价函数 J(θ) 就是上图这样的形式，我们来一点一点分析一些。其实大体都和之前逻辑函数的很类似，除了这里我们求的是 k 从 1 到 K 的所有和。这个求和项针对的是 K 个输出单元的求和，所以如果我有四个输出单元，也就是我的神经网络最后一层有四个输出单元的话，那么这个求和就是求 k 等于从 1 到 4 的每一个元素的逻辑回归算法的代价函数的和。然后最后面那项就类似于我们在逻辑回归里所用的正则化项。

值得一提的是，正如我们在逻辑回归里一样，这里的计算也要除去那些对应于偏差单元的偏差值，具体地说我们不把那些i = 0的项加入其中，这是偏差单元的项可以类比于我们在做逻辑回归的时候，我们就不把这些项加入到正规化项里去，因为我们并不想正规化这些项，这些项的值永远都是 1 ，是不会发生变化的。但即使我们真的把他们加进去了，也不会有大的差异，但是这个"不把偏差项正规化" 的规定可能只是会更常见一些。

以上就是神经网络代价函数的相关内容，下面我们来看看如何进行求解。

反向传播

在上一部分，我们一同学习了神经网络的代价函数，现在就让我们一起来学习让代价函数最小化的算法——反向传播算法。下图是我们上一部分讲到的代价函数，我们要做的就是设法找到使得J(θ)取到最小值的对应参数：

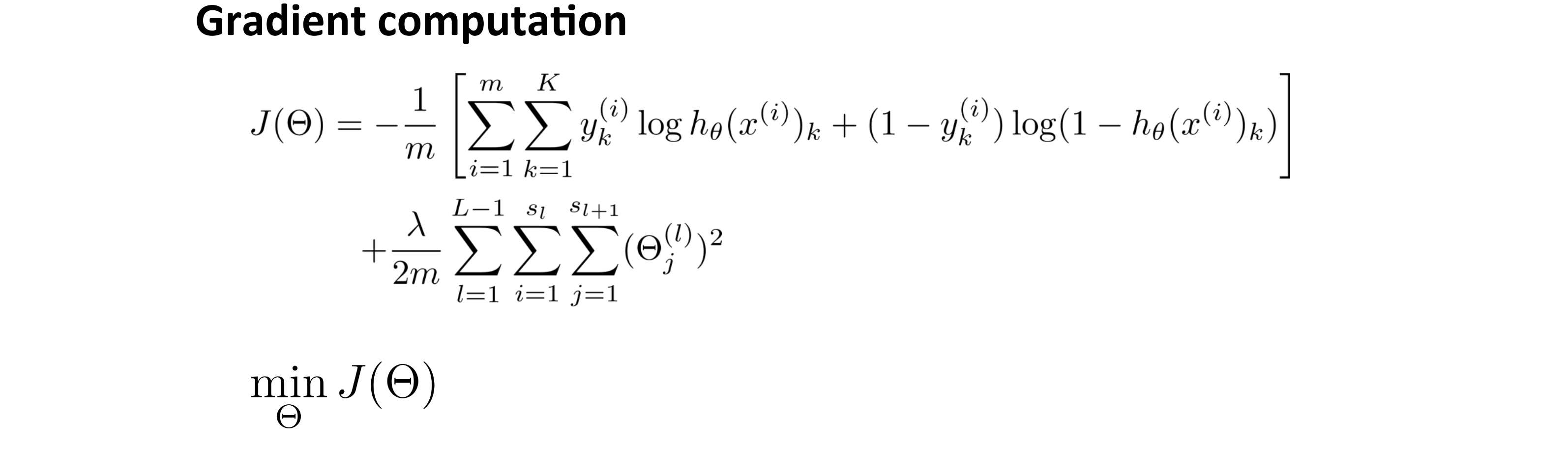
为了使用梯度下降法或者其他某种高级优化算法，我们需要做的就是写一个可以通过输入参数 θ 来计算 J(θ) 和偏导数项的代码：

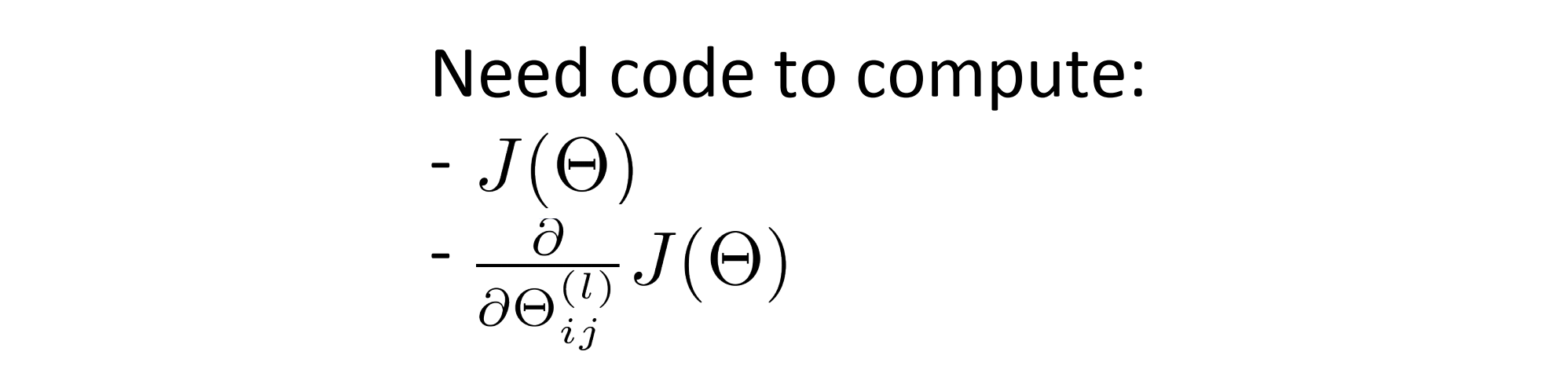
由于 J(θ) 的公式已经给出，很好计算，我们的重点是要关注如何计算这些偏导数项。我们从只有一个训练样本的情况 开始说起：假设我们整个训练集只包含一个训练样本(x, y)。 让我们来看看如何计算。首先我们应用前向传播方来 计算一下在给定输入的时候假设函数的输出结果，就如下图：

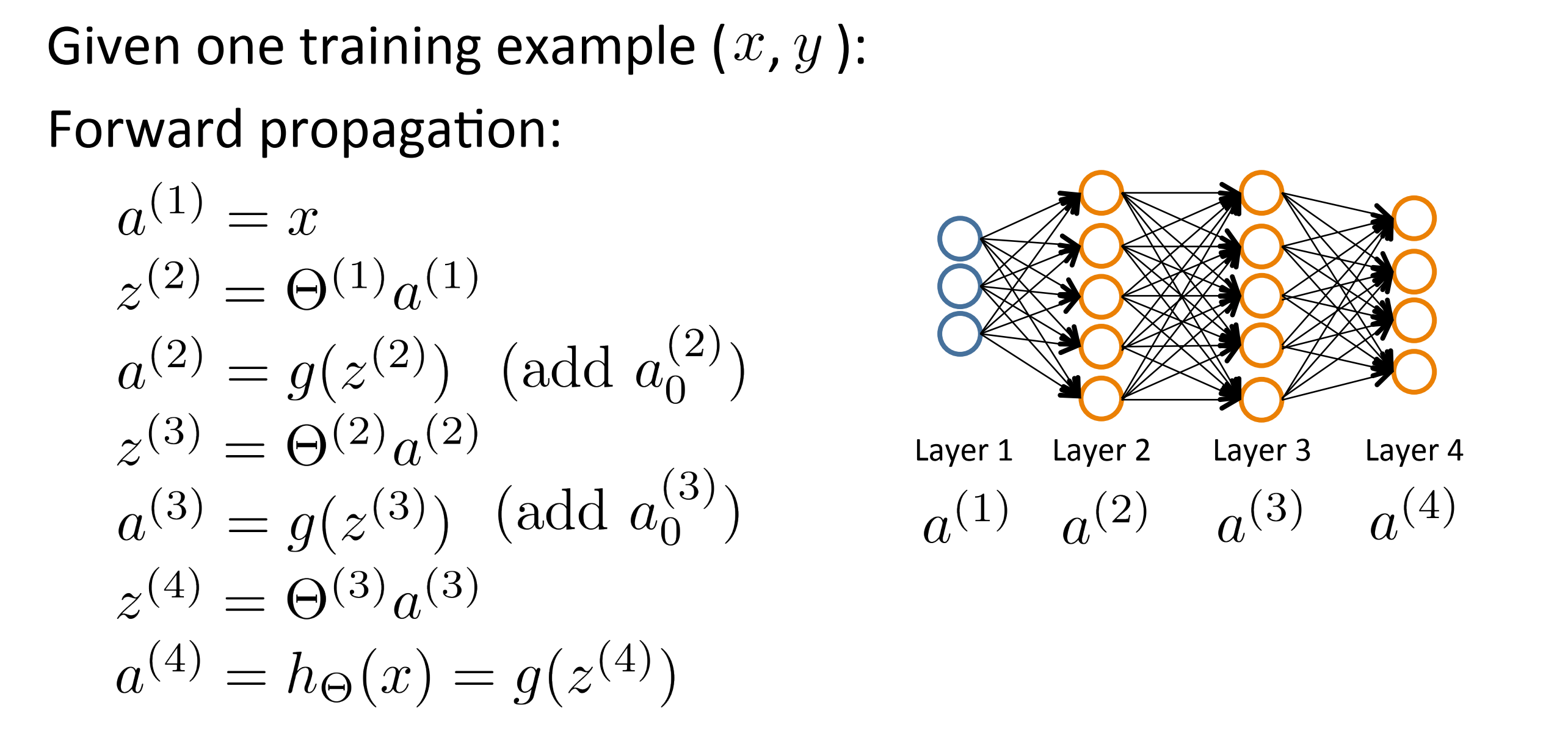
具体地说 这里的 a(1) 就是第一层的激励值，也就是输入层在的地方，其值就是 x 。然后我们来计算 z(2) ，其值等于 θ(1) * a(1) 然后 a(2) = g(z(2)) 函数，其中 g 是一个S型激励函数，这就会计算出第一个隐藏层的激励值，也就是神经网络的第二层。接下来我们再用2次前向传播来计算出 a(3) 和 最后的 a(4) 。

但这里我们只是计算出了给定输入的对应结果。接下来为了计算偏导数项，我们将采用一种叫做反向传播(Backpropagation)的算法。为了实现反向传播，我们对每一个结点先计算一项 δ(l)j ，其代表了第 l 层的第 j 个结点的误差。正如 a(l)j 表示的是第 l 层第 j 个单元的 激励值，这个 δ(l)j 在某种程度上就代表到了我们在给定参数下这个神经节点的激励值的误差：

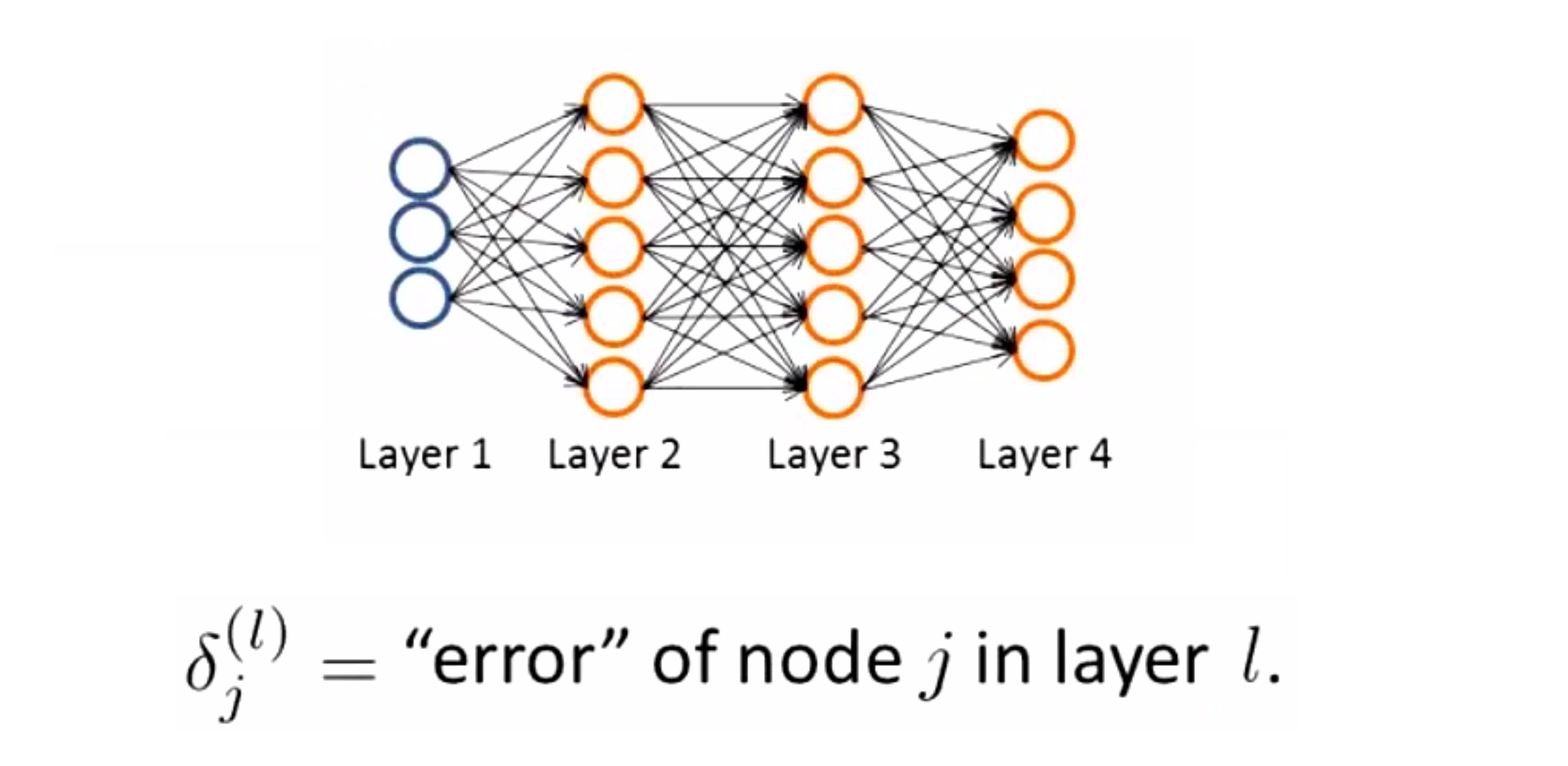
具体如何计算呢？我们用上图的神经网络结构做为例子。对于每一个输出单元，我们准备计算δ项，计算过程就如下：

所下面我们一层一层进行讲解。首先第四层的第 j 个单元的 δ 就等于这个单元的激励值减去训练样本里的真实值，即 a(4)j - yj。我们下一步就是计算网络中前面几层的误差项 δ ，根据数学推导我们发现 δ(3) = θ(3)^T * δ(4) * g'(z(3)),这里的 θ(3)^T * δ(4) 的乘法代表的是向量的点乘，其得到的向量的每个元素是两个向量对应元素的乘积，而 g'(z(3)) 同样也是一个向量，所以后面那个乘法也是一个点乘。如果你掌握微积分的话你可以试着自己解出g'(z(3))来，但我这里告诉你结论，其实 g'(z(3)) = a(3) * (1 - a(3)) 这里 a(3) 是激励向量，后面的 1 是以 1 为元素的向量。更一般的来说，我们有：

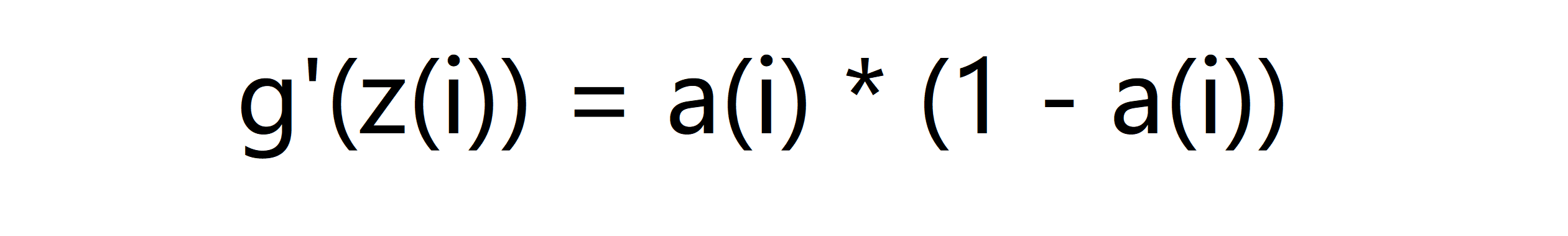
接下来我们应用一个相似的公式来计算 δ(2)。 我们的计算就到这儿结束了，这里没有 δ(1) 项是因为第一层对应的是输入层，那只是表示我们在训练集观察到的数据，所以不会存在误差。反向传播法这个名字源于我们从输出层开始计算 δ 项，然后我们一层层地返回到上一层。所以说我们是类似于把输出层的误差反向传播给了上一层，然后是再传到上上层……这就是反向传播的意思。

最后这个反向传播过程的推导过程是出奇的麻烦的，但是如果你抛弃证明，直接按照这样几个步骤计算，就有可能简单直接地完成复杂的数学计算，也能得到不错的效果。并且如果你忽略正则化所产生的项，我们可以证明我们要求的偏导数项恰好就等于激励函数和这些 δ 项的乘积，即：

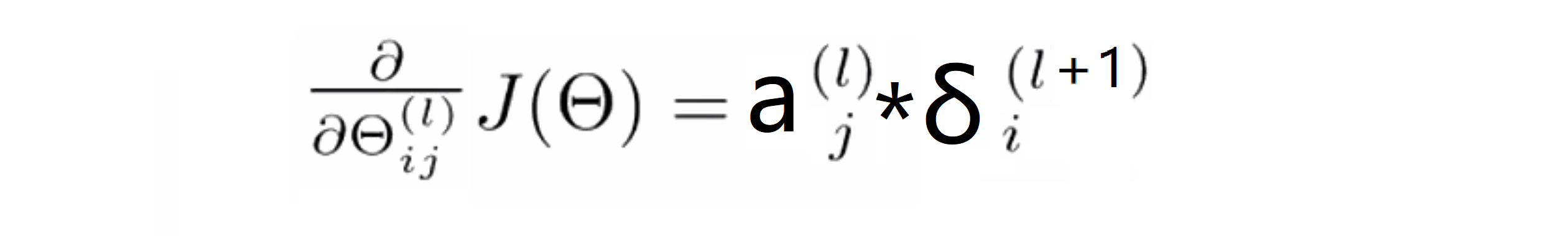
所以通过反向传播，我们可以非常快速的计算出所有参数的 偏导数项。接下来我们来看看当我们有一个非常大的训练样本时，而不是像我们例子里这样的一个训练样本我们是怎么样操做的。假设我们有 m 个样本的训练，正如下图所写，我要做的第一件事就是对于每个点定义一个 Δij 并且初始化为 0 ，而这些 Δij 会被用来计算偏导数项：

接下来我们将用 for 循环遍历我们的训练集：

我们来分析一下我们要在循环内干什么。我们将取训练样本 (x(i), y(i)) ，我们要做的第一件事是设定 a(1) 也就是输入层的激励函数，设定它等于 x(i)。x(i) 就是我们第 i 个训练样本的输入值。接下来我们运用正向传播来计算第二层的激励值，然后是第三层，第四层一直到最后一层L层的激励值。接下来我们将用我们这个样本的结果值 y(i) 和我们前向传播计算出来的结果 a(L) 来计算这个输出值所对应的误差项 δ(L) = a(L) - y(i)。接下来我们将运用反向传播算法来计算 δ(L-1) δ(L-2) 一直这样直到 δ(2)。再强调一下这里没有 δ(1) ，因为我们不需要对输入层考虑误差项。最后我们将用 Δij 来累加我们在前面写好的偏导数项。顺便说一下我们可以把最后那个表达式写成向量形式，即：

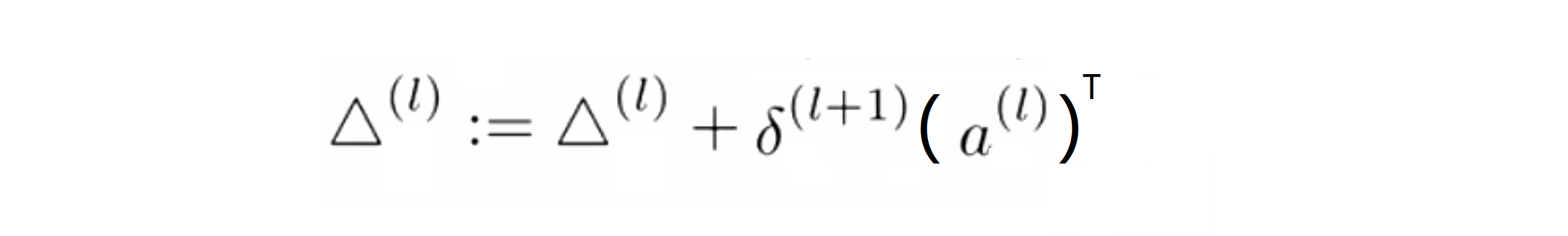
最后执行这个 for 循环体之后，我们跳出这个 for 循环，然后计算下面这些式子：

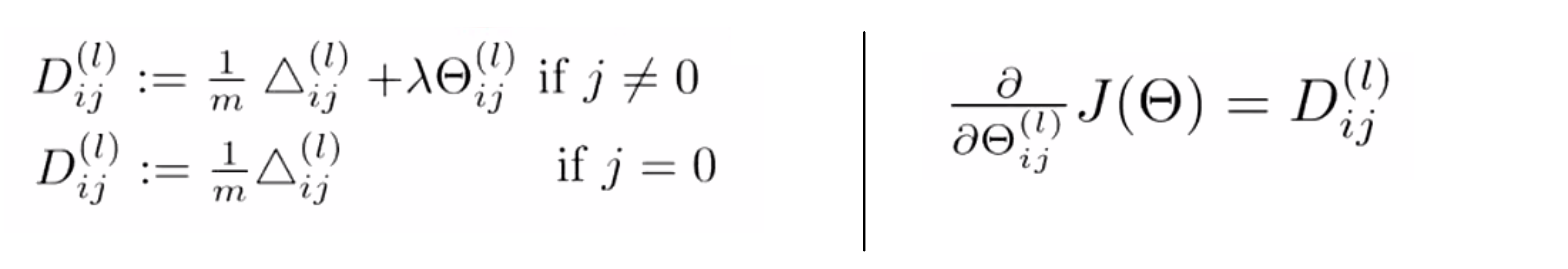
我们按照上面的公式计算 j=0 和 j≠0 的两种情况。最后尽管严格的证明对于我们来说太复杂，但是现在可以说明的是，一旦我们计算出来了这些，我们可以把他们用在梯度下降法或者其他一种更高级的优化算法上，而不需要详细的证明。

这就是反向传播算法的详细计算过程，下一部分我会尝试带领你再去深入理解反向传播的细节含义。

反向传播的理解

在之前的部分中，我们介绍了反向传播算法，这是一个非常复杂的算法，比较难以理解。所以下面我们再再一步一步来理解这个算法，希望能让你更有体会。

为了更好地理解反向传播算法，让我们先来看看正向传播。我们以下图这个神经网络作为例子：

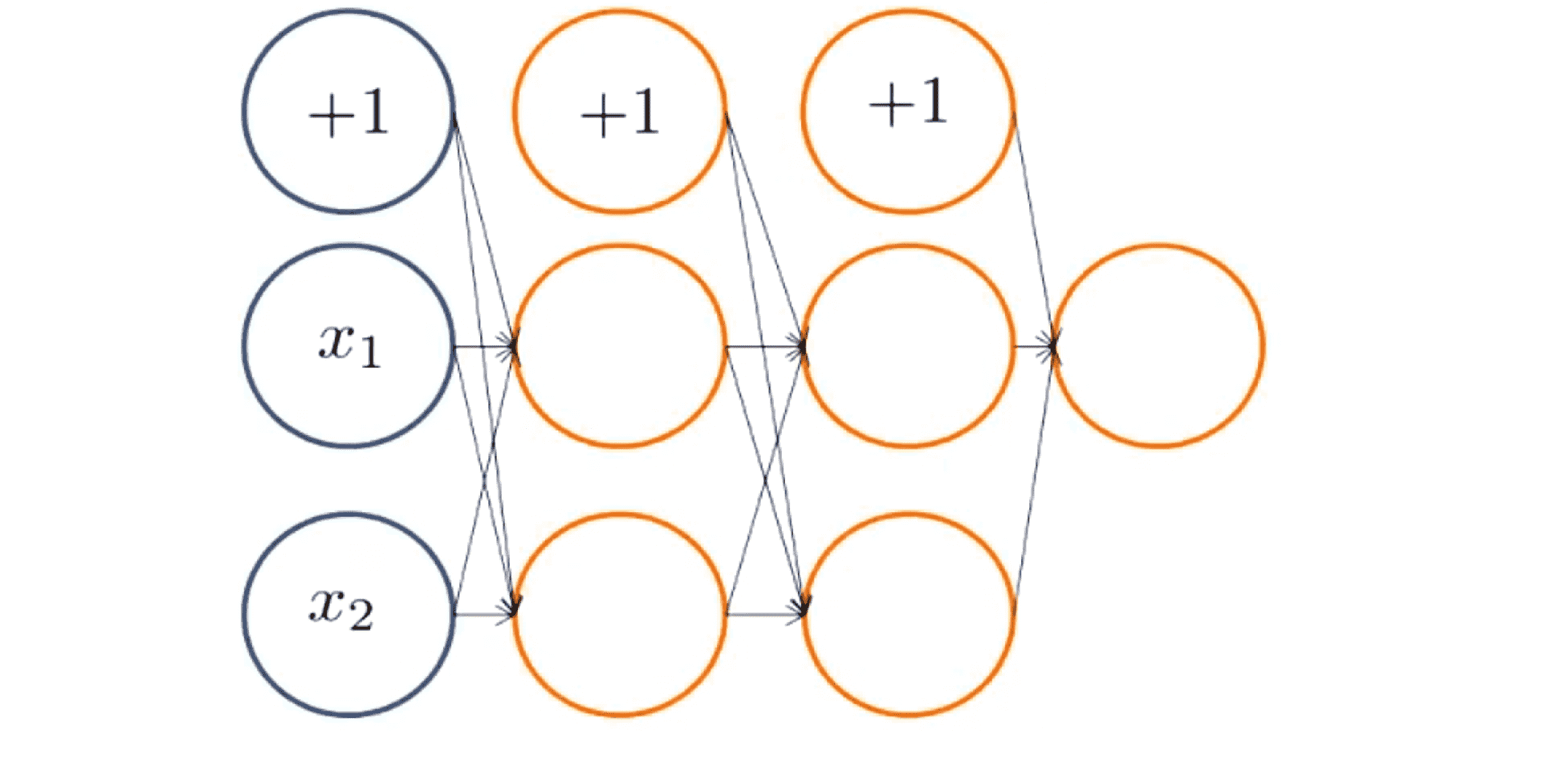
这个神经网络有两个输入层单元（不算上偏置单元），两层每层两个隐层单元，还有一个输出单元。还记得前向传播是怎么计算的吗？我们将把 xi，yi 输入到这个网络当中，xi1 和 xi2 将是我们对输入层的激励值。当我们的传播进入第一个隐层，我们会计算 z(2)1 和 z(2)2 ，然后通过 g 函数作用于z(2)1 和 z(2)2，我们就得到了 a(2)1 和 a(2)2 ……如此重复下去，直到最后一层。

下面我们举个例子，就拿 z(3)1 的计算作为例子吧：

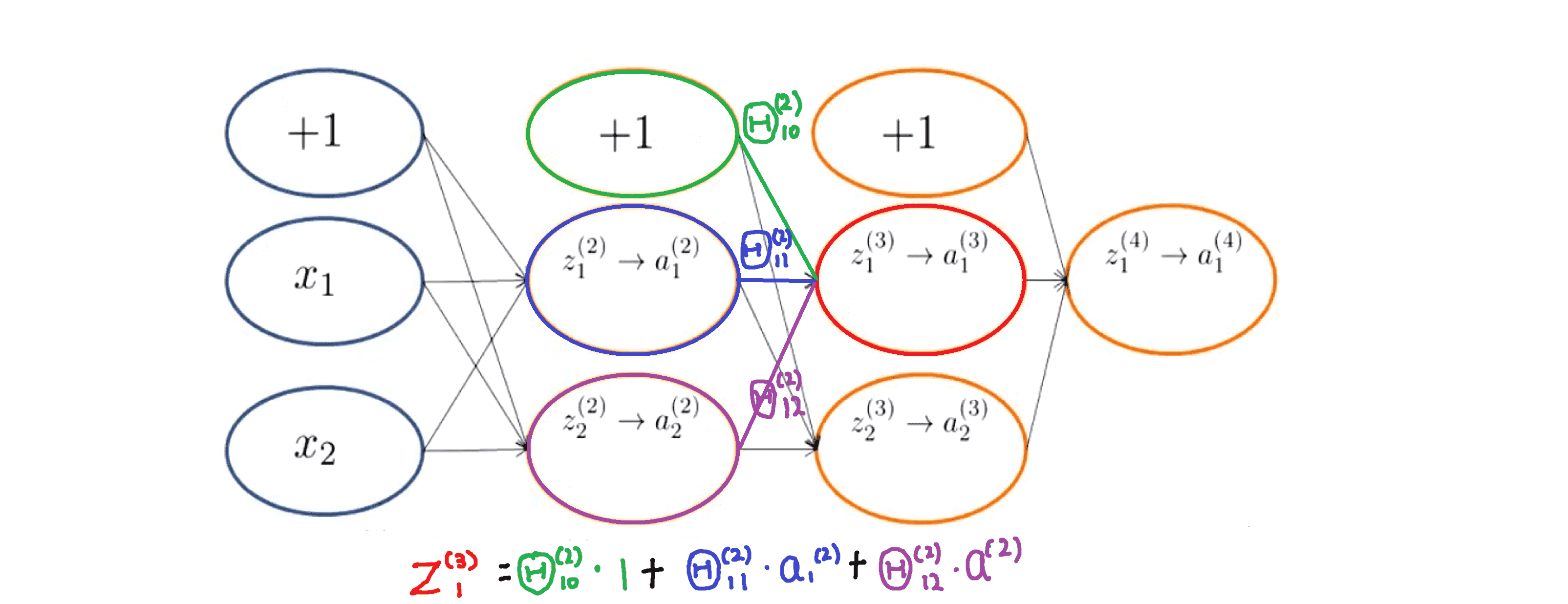
z(3)1的值与上一层的三个神经元有关，我们由图可以看到 z(3)1 = Θ(2)10 * 1 + Θ(2)11 * a(2)1 + Θ(2)12 * a(2)2。即其值是上一层神经元关于 Θ(2)1 的一个线性组合。

而反向传播做的事情其实也很类似，区别就是前向传播的计算从左到右，而反向传播的计算是从右到左。首先来看其代价函数：

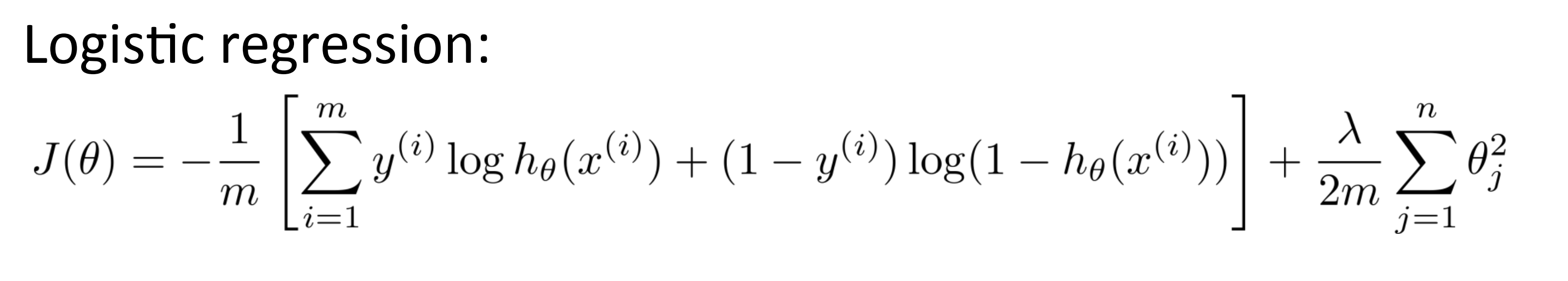
这是只有一个输出单元时候的支付函数，如果我们有多个输入单元，那就需要将输入单元进行求和：

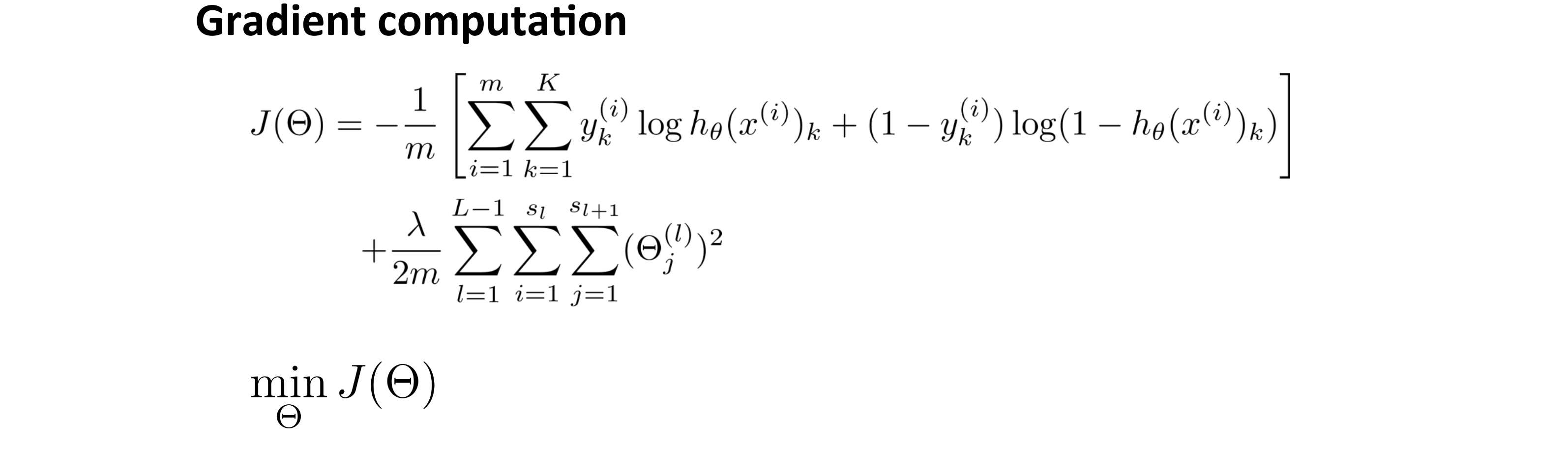
如果只有一个，用上面这个函数就行。我们用同样的神经网络例子来展示后向传播，我们来关注一个训练样本 x(i) 和 y(i)，我们现在不考虑标准化，所以 λ = 0 我们对这个样本的代价计算公式就如下：

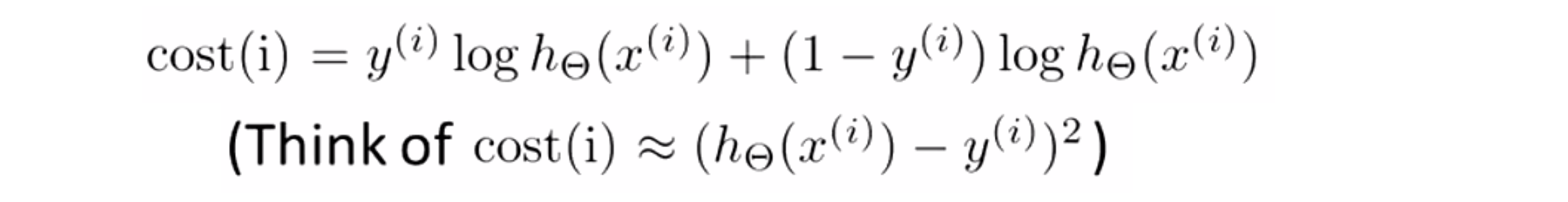
我们发现这个代价函数的值只和我们的训练数据 x(i) 和 y(i) 有关。这和我们的逻辑回归是很像的，如果我们不看之前那个复杂的表达式，只看一个样本，这其实就是平方误差函数。所以 cost(i )描述了这个网络的误差，代表了对特定的结果 i 那么到底这个计算结果和真实值 y(i) 的拟合程度。

所以我们的代价函数就解释得通了。下面让我们来看看反向传播的作用。反向传播的目的其实就是计算 δj ，那我们为什么要计算 δj 呢，其实它就是 z(l)j 的一个偏微分：

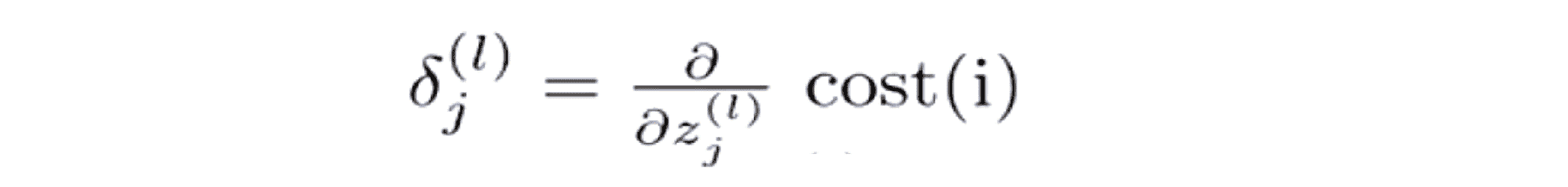
如果你熟悉偏微分，你就知道对代价函数的偏微分中的一部分就是 δj ，所以 δj 在一定程度上衡量了我们要如果改变网络的权值会产生的影响，所以我们要去计算它。接下来让我们来看看到底反向传播算法是怎么具体计算的。

首先，δ(4)1 正如y(i)我们对前向传播算法和后向传播对训练数据 i 的做法一样，其表达的是 δ(4)1 = y(i) - a(4)1接下来，我们来把这些值反向传播回去,得到δ(3)1 和 δ3(2)，然后我们进一步往前，得到 δ(2)1 和 δ(2)2 。这看起来就像是又重演前向传播只不过我们现在反过来做了。

我们还是举个例子看看具体是如何得到 δ(2)2 的：

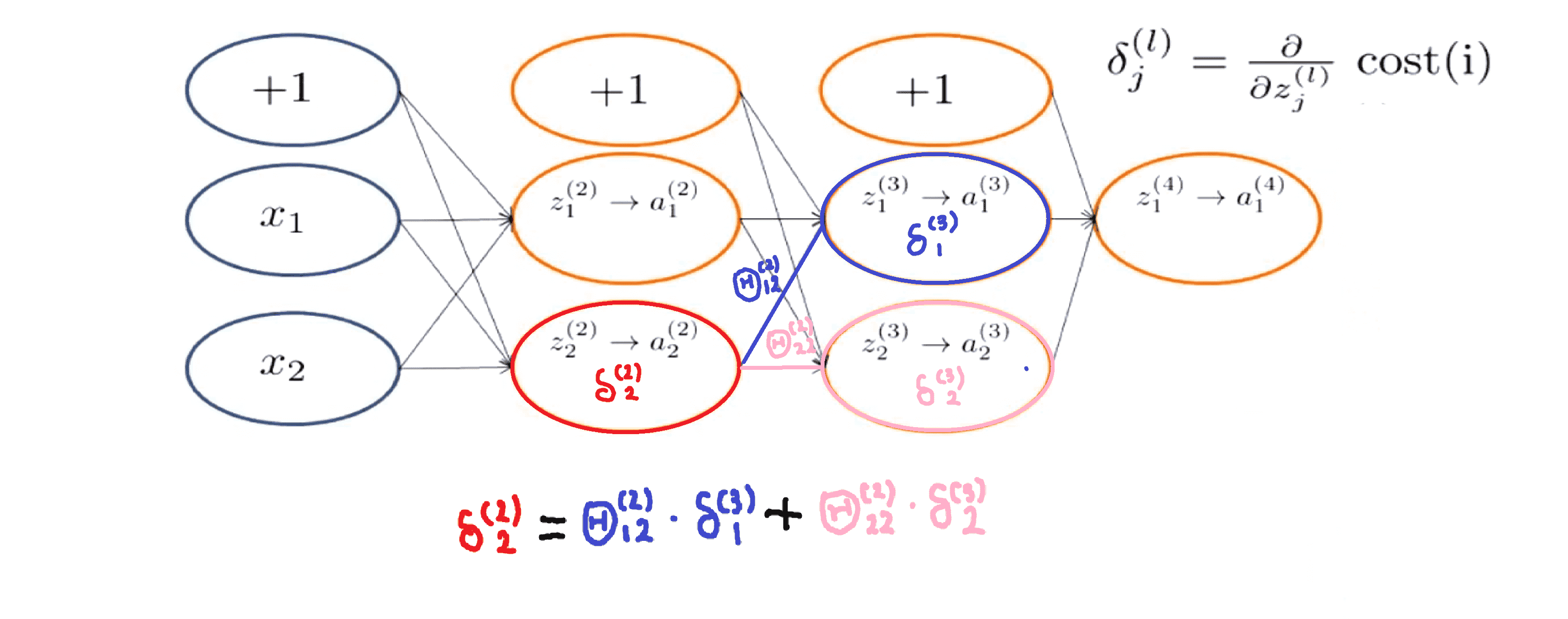
我们观察与δ所在神经元相连的后层单元，我们发现，其实其计算过程与前向传播类似， δ(2)2 = Θ(2)12 * δ(3)1 * Θ(2)22 * δ(3)2。这就是反向传播的完整过程。

结语

通过这篇BLOG，相信你已经初步掌握了神经网络代价函数与反向传播的相关知识，后续我们还会继续进行讲解。最后希望你喜欢这篇BLOG！