在之前的BLOG里,我们介绍了神经网络的概况和背景。在这篇BLOG,我们将会探寻神经网络的一些表达方式,为之后的算法学习做准备。
从大脑神经到神经网络
这一部分,就让我们看看该如何表示神经网络,换句话说当我们在运用神经网络时,该如何表示我们的假设或模型。
神经网络是在模仿大脑中的神经元或者神经网络时发明的,因此要解释如何表示模型假设,我们先来看单个神经元在大脑中是什么样的:
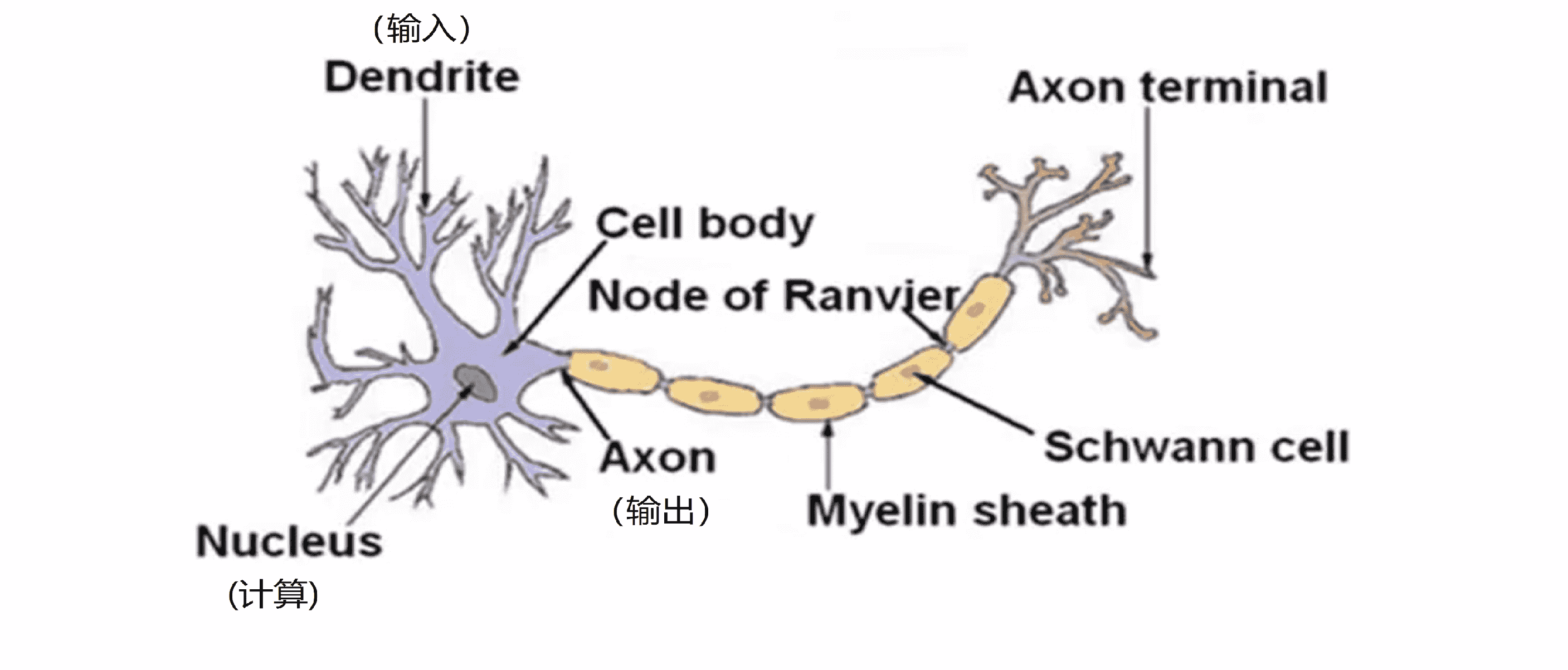
我们的大脑中充满了上图这样的神经元,神经元是大脑中的一种特殊的细胞。其中有两点值得我们注意,一是神经元有细胞主体;二是神经元有一定数量的输入神经,也就是树突。可以把它们把树突想象成输入电线,它们接收来自其他神经元的信息;三是神经元有输出神经即轴突,这些输出神经是用来给其他神经元传递信号的。简而言之,神经元可以看成是一个计算单元,它从输入神经接受一定数目的信息并做一些计算,然后将结果通过它的轴突传送到其他节点或者大脑中的其他神经元。
下图是一组神经元的示意图:
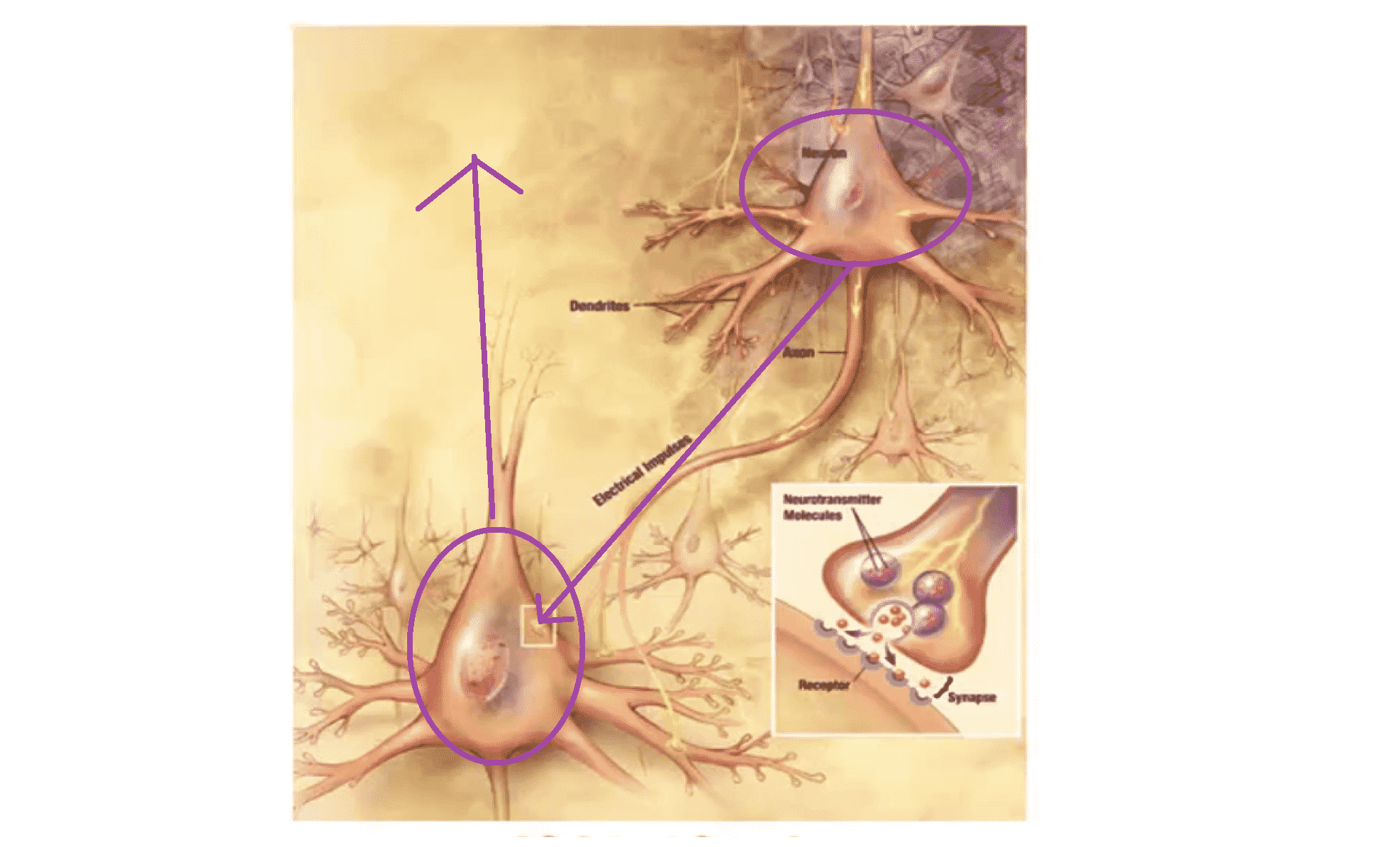
我们可以看到神经元利用微弱的电流进行沟通,这些弱电流也称作动作电位。如果上面那个神经元想要传递一个消息给下面,它就会就通过它的轴突发送一段微弱电流给下面那个神经元。而下面那个神经元通过其树突接收这条消息,然后做一些计算后,再将处理过后的消息传给其他神经元。这就是神经元信息传递的模型。
所以说,我们在电脑上实现的人工神经网络时,我们也将使用一个非常简单的模型来模拟神经元的工作,如下图:
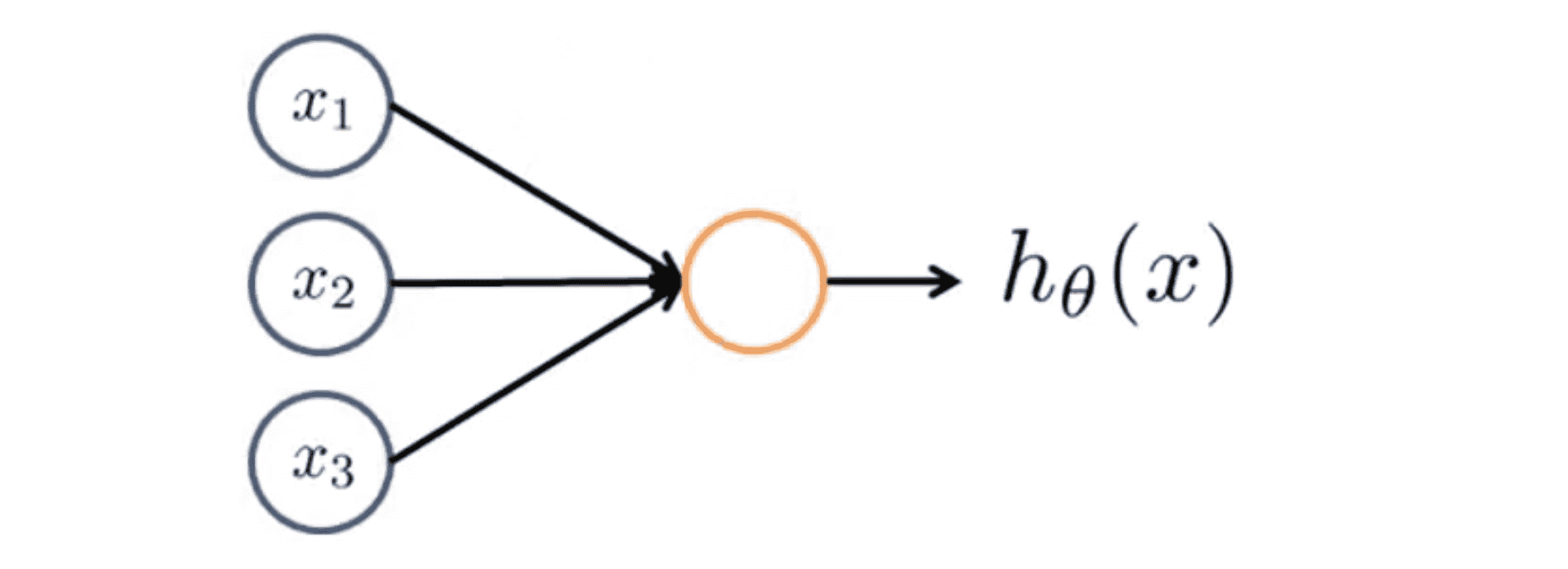
我们将神经元模拟成一个逻辑单元,就像上图中的黄色圆圈,然后我们通过它的树突或者说它的输入神经传递给它一些信息,然后神经元做一些计算并通过它的输出神经即它的轴突输出计算结果。因为我们现在讨论的还是分类问题,所以 h(x) = 1 / (1 + e^(-θ^T * x)), 通常 x 和 θ 是我们的参数向量。这是一个简单的模型,甚至说是一个过于简单的模拟神经元的模型,它被输入 x1 x2和 x3 然后输出一些类似 h(x) 的结果。当绘制一个神经网络时,通常我们只绘制输入节点 x1 x2 x3 ,但有时也可以增加一个额外的节点 x0 ,这个 x0 节点有时也被称作偏置单位或偏置神经元,但因为 x0 总是等于1 所以可画可不画,这取决于它是否对例子有利:

现在来学习一个关于神经网络的术语,有时我们会说这是一个神经元,一个有 s 型函数或者逻辑函数作为激励函数的人工神经元。在神经网络术语中,激励函数只是对类似非线 函数 g(z) 的另一个术语称呼,其中g(z) = 1 / (1 + e^(-z)) 。到目前为止我们一直称 θ 为模型的参数,但在一些文献里,有时可能会看到其他人谈论一个模型的权重,要记住模型的权重其实和模型的参数其实是一样的东西。
上图中黄色的圆圈代表一个单一的神经, 神经网络其实就是这些不同的神经元组合在一起的集合:
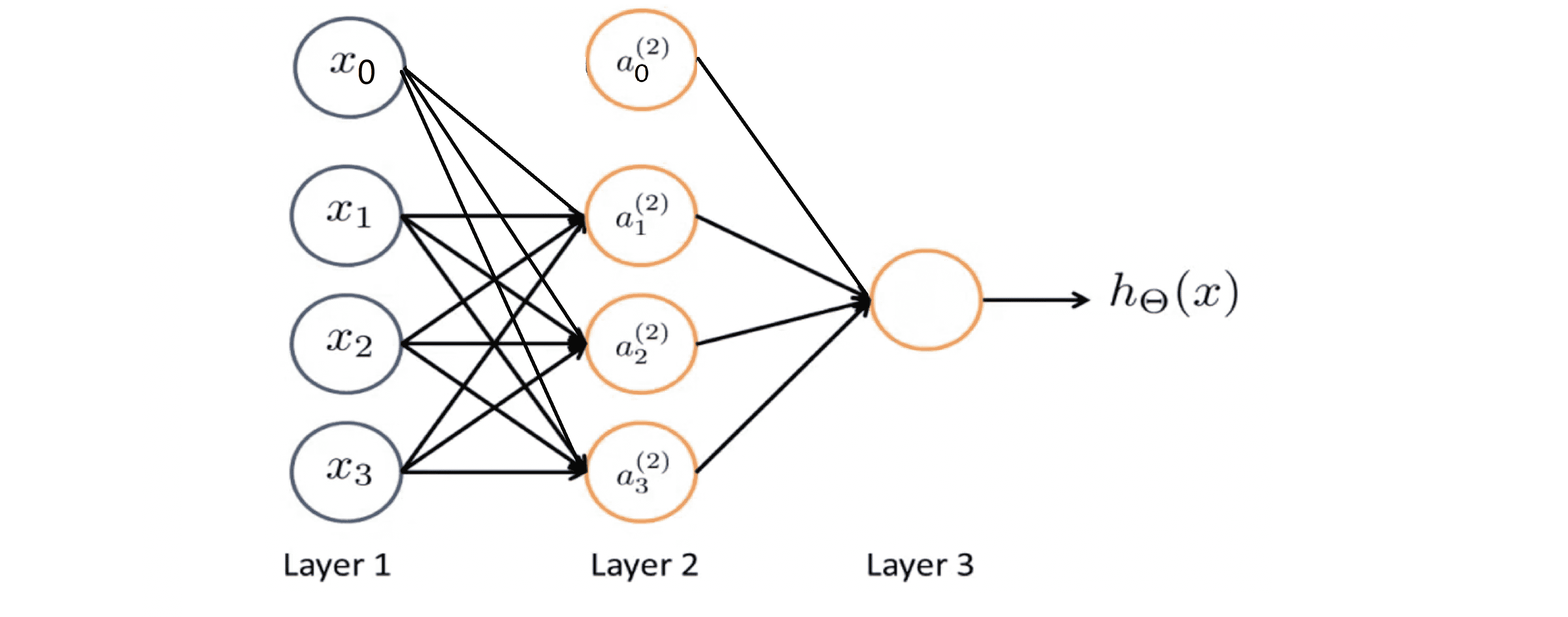
具体来说,我们第一层有输入单元x0 x1 x2和 x3 (x0 = 1),第二层有 3 个神经元我在里面写了a(2)1 a(2)2 和a(2)3 ,同样地我们也可添加一个 a(2)0 —— 一个额外的偏度单元,它的值永远是1。我们在第三层有一个神经元输出假设函数 h(x) 计算的结果。其实,网络中的第一层也被称为输入层,最后一层也称为输出层,而中间的层则被称作隐藏层。稍后我们会看到神经网络可以有不止一个的隐藏层,但在这个例子中我们有一个输入层—第1层,一个隐藏层—第2层和一个输出层—第3层。但实际上任何非输入层或非输出层的层都被称为隐藏层。
接下来我们一起来看看神经网络究竟在做什么,让我们逐步分析这个图表所呈现的计算步骤。为了解释这个神经网络具体的计算步骤,这里还有些记号要解释:

我们使用a(j)i表示第j层的第i个神经元或单元,具体来说 a(2)1 表示第2层的第一个激励,即隐藏层的第一个激励。所谓激励(activation) 是指由一个具体神经元读入计算并输出的值。此外我们的神经网络被矩阵 Θ(j) 参数化,其将成为一个波矩阵,控制着从 j 层到第 j + 1 层。
至于具体的计算过程,我们可以看下图:
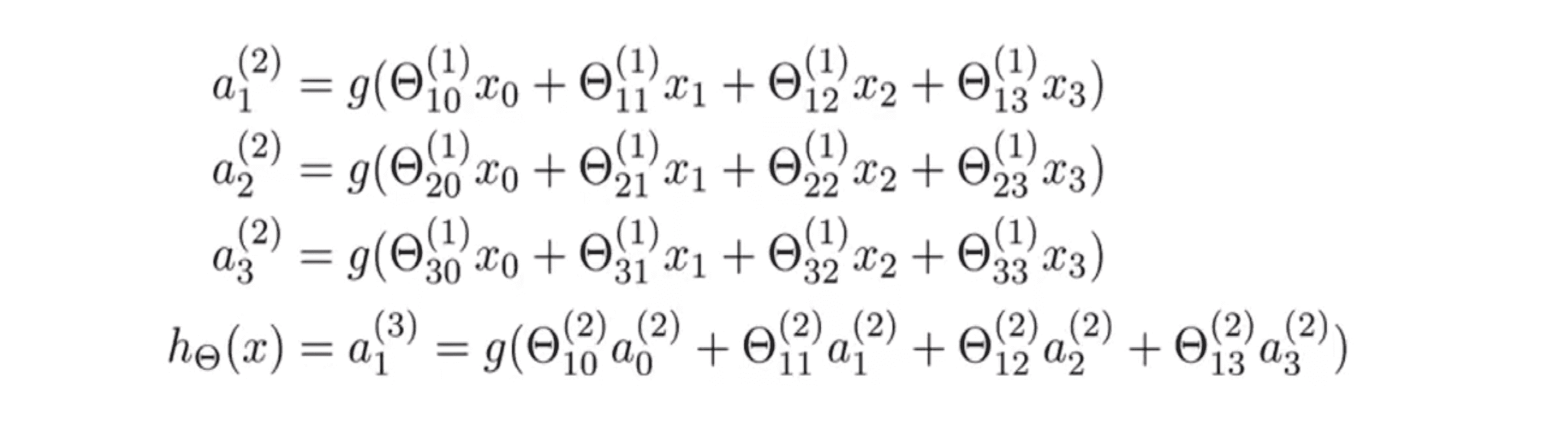
这里的第一个隐藏单元是这样计算它的值的:第一个隐藏单元 a(2)1 激励函数作用在关于 Θ(1)1 的线性组合上;第二个隐藏单元 a(2)2 激励函数作用在关于 Θ(1)2 的线性组合上;同样对于第三个,第四个隐藏的单元也是这么计算的。这么一来,参数矩阵 Θ 控制了我们来自三个输入单元到三个隐藏单元的映射,即从 x0 到 x1 映射到 a(2)1 到 a(2)2 。因此 Θ(1) 是一个3乘4维的矩阵。更一般的如果一个网络在第 j 层有 s[j] 个单元,在 j+1 层有 s[j + 1] 个单元,那么矩阵 θ(j) 即控制第j层到 第j+1层映射 的矩阵的维度为 s[j + 1] * (s[j] + 1) .
以上我们讨论了三个隐藏单位是怎么计算它们的值,最后在输出层我们还有一个单元,它计算 h(x) 。其也可以写成a(3)1。其值就等于上图中的最后一行。注意此时参数矩阵是 Θ(2) 。
总之以上我们展示了怎样定义一个人工神经网络的,接下来让我们看看假设函数的作用以加深我们的理解。
神经网络的表达和理解
这一部分,我们来看看如何高效地进行计算神经网络模型,并学习一个向量化的实现方法。更重要的是我们要一同了解为什么神经网络能帮助我们学习复杂的非线性假设。
以这个神经网络为例,之前我们说过计算出假设输出的步骤 是下面的这些方程:
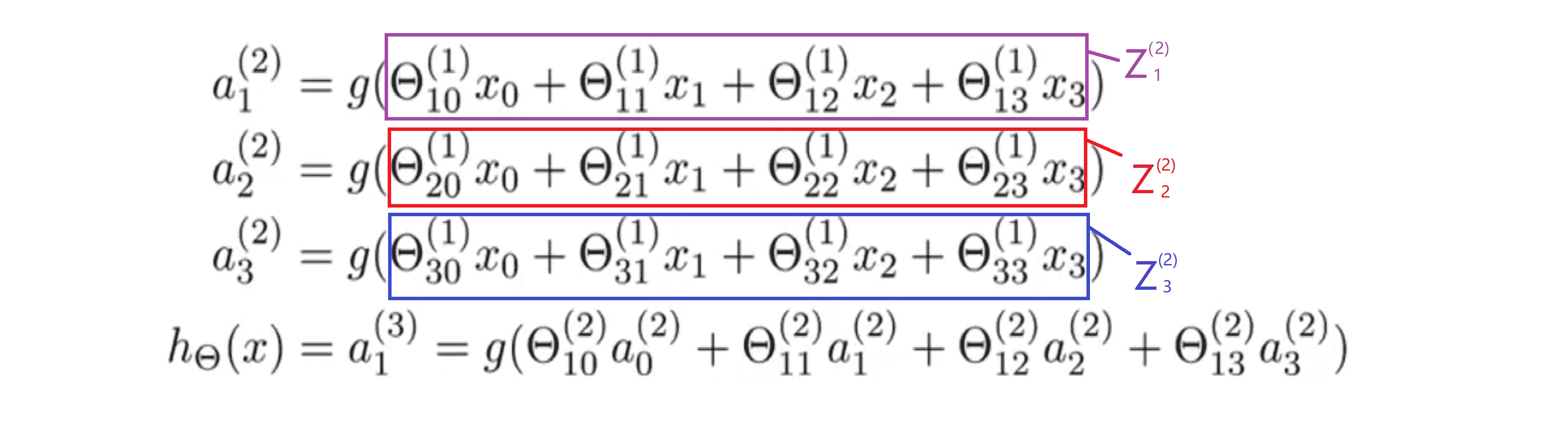
通过上面的三个方程我们计算出三个隐藏单元的激励值,然后利用这些值来计算假设函数 h(x) 的最终输出。接下来我们定义一些额外的项,我们把紫色框里的定义为 z(2)1 ,这样一来就有了 a(2)1 = g(z(2)1)。 另外顺便提一下,这些上标2的意思是在 z(2) 和 a(2) 中,即表示这些值与神经网络中的第二层相关。接下来我们同样地定义红色框中的项为 z(2)2 ,蓝色框中的项一样定义为 z(2)3。我们发现这些 z 值都是一个线性组合,即是输入值x0 x1 x2 x3的加权线性组合。
仔细看一下这一堆字母,我们可能会注意到这其实对应了矩阵向量运算,类似于矩阵向量乘法,观察到一点我们就能将神经网络的计算向量化了。具体而言我们定义特征向量 x 为x0 x1 x2 x3组成的向量,其中x0 仍然等于1。并定义 z(2) 为这些z值组成的向量即z(2)1 z(2)2 z(2)3 ,我们发现z(i) = θ(i - 1) * x,即这就为参数的向量化:
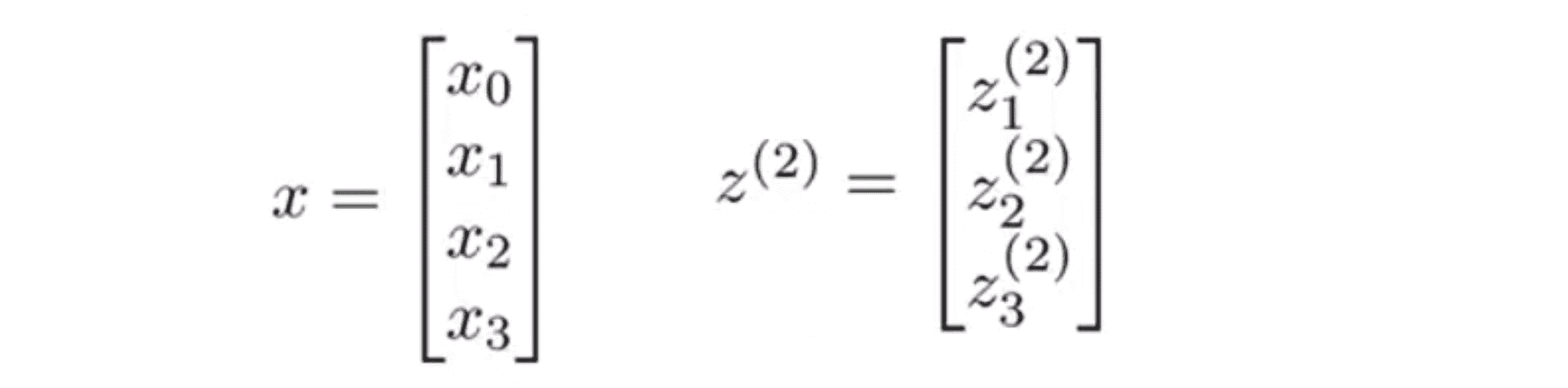
注意在这里 z(2) 是一个三维向量。下面 我们可以这样向量化a(2)1 a(2)2 a(2)3的计算。我们只用两个步骤:首先 z(2) 等于 θ(1) 乘以 x 这样就得到了向量 z(2) ,然后 a(2) 等于 g(z(2))。再次提醒,这里的 z(2) 是三维向量并且 a(2) 也是一个三维向量 。因此这里的激励 g 将 s函数逐元素作用于 z(2) 中的每个元素:
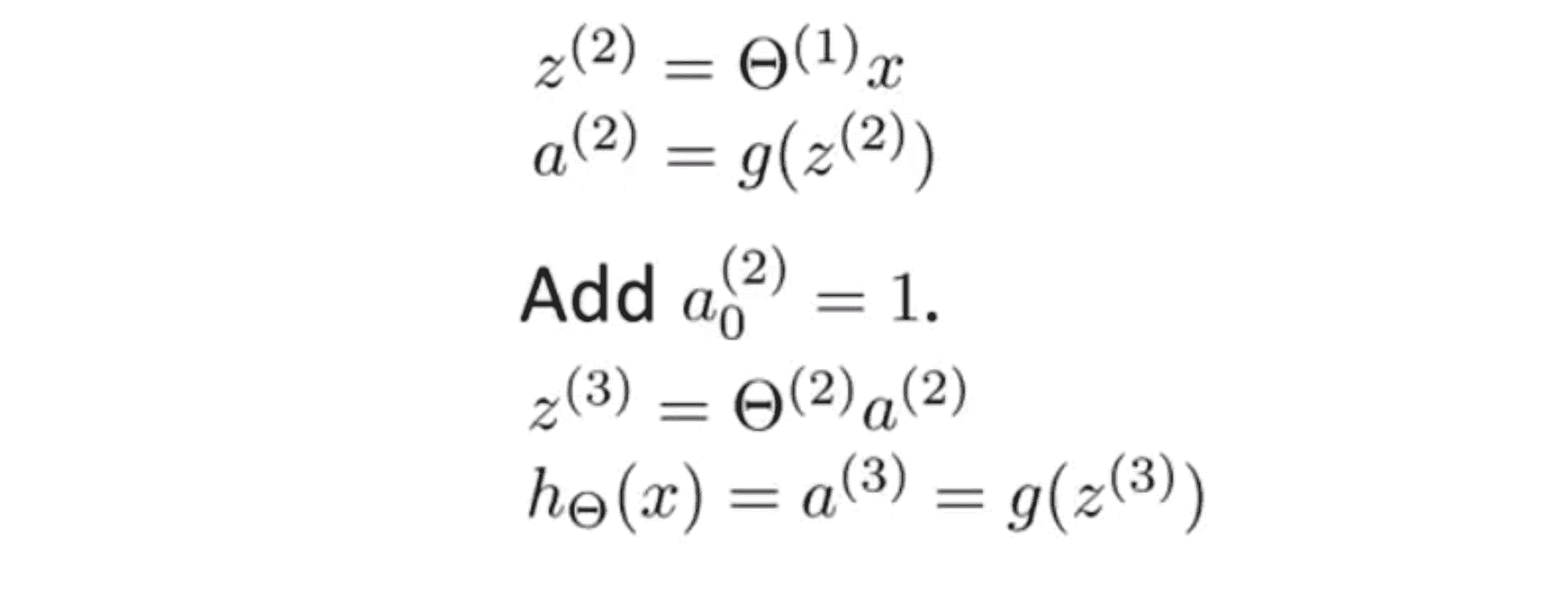
顺便说一下为了让我们的符号和接下来的工作相一致,在输入层虽然我们有输入 x ,但我们对于第三层来说还可以把第二层的数据想成是第一层的激励。所以我可以定义 a(1) 等于 x ,因此 a(1) 就是一个向量了:
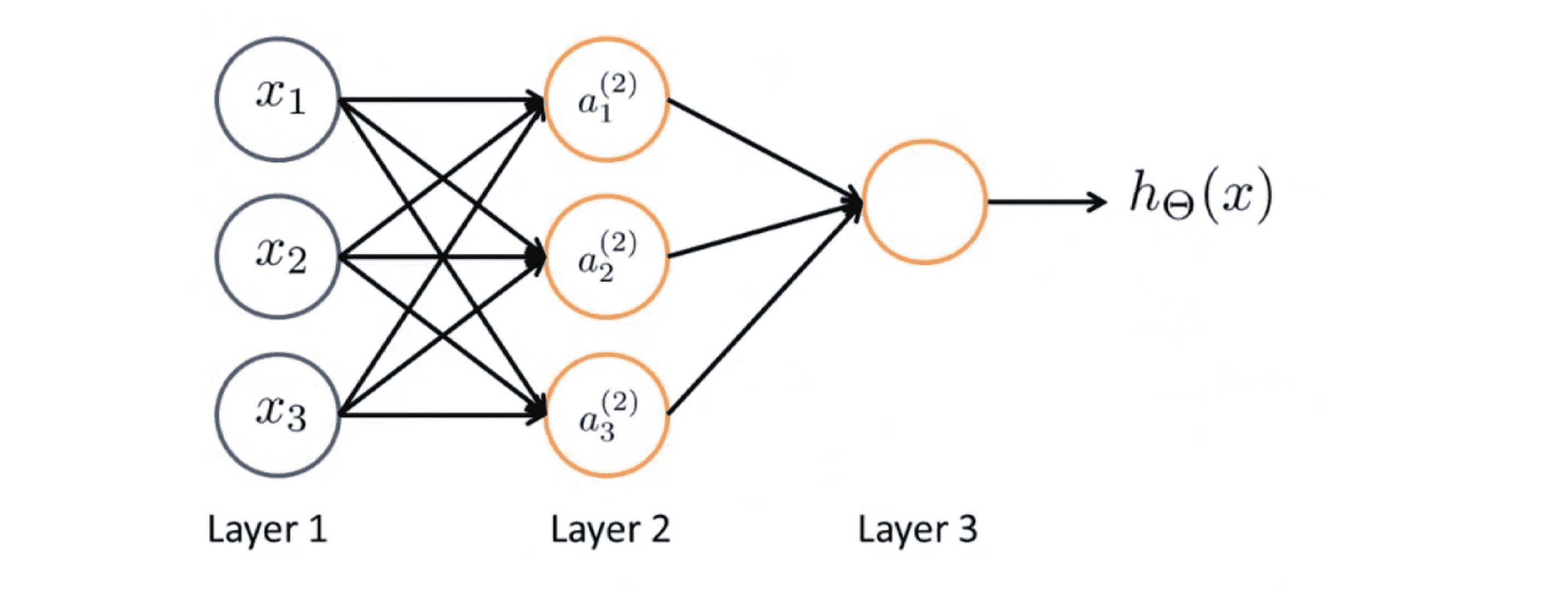
这样一来 a(2) 就是一个四维的特征向量,因为我们可以添加一个额外的 a0 它等于 1 (如下图)并且它是隐藏层的 一个偏置单元:

最后为了计算假设的实际输出值,我们只需要计算 z(3) ,即下图方程:
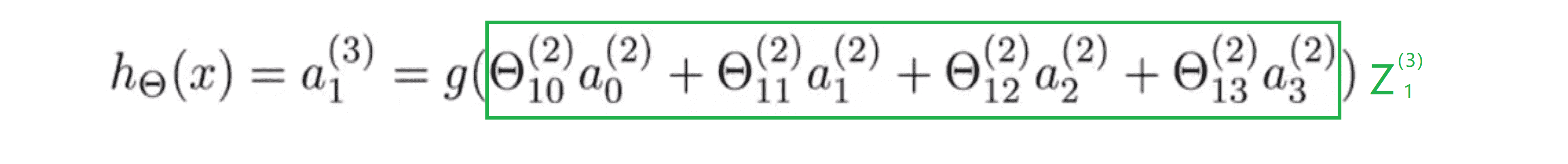
这里绿色框里的项就是 z(3),z(3) = Θ(2) * a(2) 。最后假设输出为 h(x) ,它等于 a(3)。 a(3)是输出层唯一的单元,它是一个实数你可以写成 a(3) 或 a(3)1 ,其值等于 g(z(3)) 或说是 g(z(3)1) 。
以上这个计算h(x)的过程被称为前向传播(forward propagation) 。这样命名是因为我们从输入层的激励开始进行前向传播,传播给隐藏层并计算隐藏层的激励后,继续前向传播给输出层并计算输出层的激励,最后输出。这个从输入层到隐藏层再到输出层依次计算激励的过程叫前向传播。我们刚刚学会了这一过程的向量化的实现方法,如果我们使用之前的那些公式实现它,就会得到一个有效的计算h(x) 的方法。
这种前向传播的角度也可以帮助我们了解神经网络的原理,及它为什么能够帮助我们学习非线性假设。看一下下面这个神经网络,我们先暂时盖住图片的左边部分:
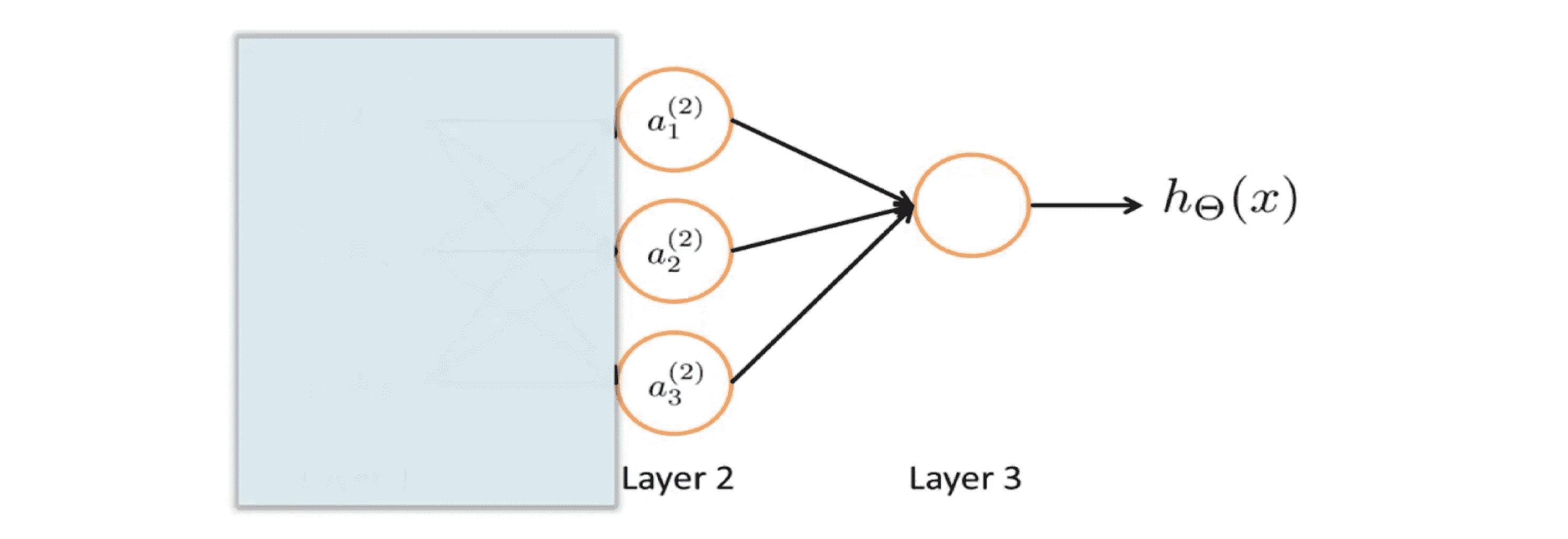
如果我们观察图中剩下的部分,就看起来很像逻辑回归,在逻辑回归中,我们用一个节点即逻辑回归单元,来预测 h(x)的值。具体来说假设输出的 h(x)将等于s型激励函数 g(Θ0 * a0 + Θ1 * a1 +Θ2 * a2 +Θ3 * a3), 其中 a1 a2 a3 由这第二层的三个单元给出。因为我只有一个输出单元,但如果你忽略蓝色的部分,看起来就非常像标准的 逻辑回归模型。不同之处在于我现在用的是大写的 Θ 而不是小写的 θ。这样做完我们只得到了逻辑回归,但是这次逻辑回归的输入特征值是通过隐藏层计算的:

所以神经网络所做的就像普通的逻辑回归,但是它 不是使用 x1 x2 x3作为输入特征,而是用a1 a2 a3作为新的输入特征。有趣的是特征项a1 a2 a3它们是作为输入的函数来学习的。具体来说其值就是从第一层映射到第二层的函数,这个函数的线性组合方法由其他一组参数 Θ(1) 来决定。所以在神经网络中,我们没有直接用输入特征x1 x2 x3 来训练逻辑回归,而是自己训练逻辑回归的结果 a1 a2 a3 作为输入。
所以,如果在 Θ1 中选择不同的参数,有时可以学习到一些很有趣和复杂的特征,就可以得到一些更好的假设,比使用原始输入 x1 x2 x3 时得到的假设更好。你也可以选择多项式项 x1 x2 x3 等作为输入项,但这个算法可以灵活地快速学习任意的特征项,把这些 a1 a2 a3 输入最后一层的单元,实际上其做的就是逻辑回归。
顺带一提,我们还可以用其他类型的图来表示神经网络,神经网络中神经元相连接的方式被称为神经网络的架构。所以说架构是指不同的神经元是如何相互连接的。下面有一个不同的神经网络架构的例子:
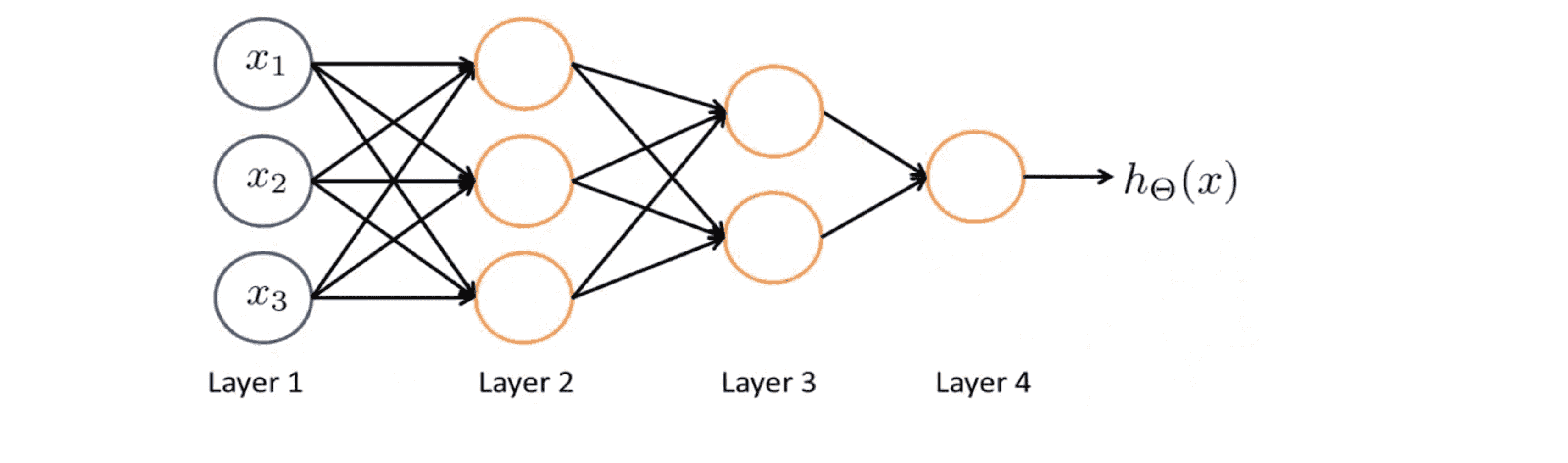
在这里,我们有两层的隐藏层——第二层和第三层。第二层中,我们有三个隐藏单元,它们根据输入层计算一个复杂的函数,然后第三层,两个神经单元可以将第二层训练出的特征项作为输入,并在第三层计算一些更复杂的函数。这样在我们到达输出层时,我们就可以利用第三层训练出的更复杂的特征项作为输入,以此得到更加有趣的非线性假设。
这就是神经网络工作的大致原理。
结语
通过这篇BLOG,相信你已经大致理解前向传播在神经网络里的工作原理, 也知道了如何向量化这些计算。在之后的BLOG里,我们会就如何使用神经网络举出两个实际的例子。最后希望你喜欢这篇BLOG!