在之前的BLOG里，我们介绍了神经网络的大致原理。 现在就让我们一起来看看其中的一些实现技巧吧！

矩阵展开

在神经网络反向传播的过程中，我们需要将参数从矩阵展开成向量，以便我们在高级最优化步骤中的使用需要，我们称这个将矩阵展开成向量的过程为过程是矩阵展开。

具体来讲，为了使用 Octave 自带的高级优化算法，我们需要自己编写代价函数 costFunction ：

function [jVal, gradient] = costFunction(theta)
………………
optTheta = fminunc(@costFunction, initialTheta, options)

我们这个函数的输入参数是theta，返回值是代价函数以及偏导数值，然后我们将返回的值传递给高级最优化算法。顺便提醒一下 fminunc 并不是唯一的高级优化算法，我们也可以使用别的优化算法，但它们都需要我们编写类似的代价函数和偏导数的函数。现在我们来看看这个代价函数，我们的传入值 theta 是一个 n 阶或者 n + 1 阶的向量，同时我们函数的返回值，也就是jVal 和 gradient值，也是 n 阶或者 n + 1 阶的向量。问题就出现在这里，对于神经网络，我们的参数 Θ 将不再是向量，而是矩阵了，因此对于一个完整的神经网络，我们的参数矩阵为Θ(1) Θ(2) Θ(3)，在Octave中我们可以设为 Theta1 Theta2 Theta3之类的；类似地，这些梯度项 gradient 也是以梯度矩阵的形式出现， 我们一般记为D(1) D(2) D(3)，在Octave中我们用矩阵D1 D2 D3来表示：

接下来看看我们如何将我们的矩阵转化为向量。举个例子，假设我们有下图这样一个神经网络：

在这个例子中，我们的输入层有 10 个输入单元，隐藏层有一层 10 个单元，最后输出层只有一个输出单元。我们记 s1 等于第一层的单元数， s2 等于第二层的单元数，s3 等于第三层的单元个数。在这种情况下，矩阵θ的维度和矩阵D的维度就已经确定了，比如说 θ(1) 就是一个10x11的矩阵，以此类推。

因此在Octave中，如果我们想将这些矩阵转化为向量，那么我们要做的就是取出你的Theta1 Theta2 Theta3，然后使用下面这段代码：

thetaVec = [ Theta1(:); Theta2(:); Theta3(:)];
DVec = [D1(:); D2(:); D3(:)];

对于 D 也同理。上面代码将取出三个 θ 矩阵中的所有元素，然后把它们全部展开成为一个很长的向量。同样地第二行的代码将取出 D 矩阵的所有元素然后展开成为一个很长的向量。

接着如果我们想从向量表达返回到矩阵表达式的话，我们要做的是，比如想再得到 Theta1 那么我们取出取 thetaVec 的前110个元素，再重新组合成一个10x11的矩阵，我们可以用 reshape 命令来重新得到Theta1，同样类似的要重新得到Theta2矩阵，我们需要抽出下一组110个元素并且重新组合，然后对于Theta3，我们只需要抽出最后11个元素然后执行reshape命令：

Theta1 = reshape(thetaVec(1:110),10,11);
Theta2 = reshape(thetaVec(111:220),10,11);
Theta3 = reshape(thetaVec(221:231),1,11);

以下是这一过程的Octave演示，对于这一个例子让我们假设Theta1 为一个10x11的矩阵，其每一项都为1 ，Theta2设为一个10行11列矩阵每个元素都为2，然后设 Theta3 是一个1x11的矩阵，每个元素都为3。现在我们想把所有这些矩阵变成一个向量 thetaVec = [Theta1(:); Theta2(:); Theta3(:)]; 现在thetaVec矩阵就变成了一个很长的向量，含有231个元素：

接下来我们可以对thetaVec使用reshape命令抽出前110个元素将它们重组为一个10x11的矩阵，这样我又再次得到了Theta1矩阵：

对Theta2 和 Theta3 也同理。下面我们来看怎样将这一方法应用于我们的学习算法。假设我们有一些初始参数值 θ(1) θ(2) θ(3) ，我们要做的是取出这些参数并且将它们 展开为一个长向量，我们称之为initialTheta 然后作为theta参数的初始设置传入函数fminunc。我们要做的另一件事是执行代价函数 costFunction 实现算法如下：

function [jval, gradientVec] = costFunction(thetaVec)
    From thetaVec, get Θ(1) Θ(2) Θ(3)
    Use forward prop/back prop to compute D(1) D(2) D(3)
    and Unroll D(1) D(2) D(3) to get gradientVec.

我们下面来进行解释。代价函数 costFunction 将传入参数 thetaVec ——一个包含我所有参数的向量。因此我们要做的第一件事是使用 thetaVec 和重组函数 reshape 。因此我要抽出 thetaVec 中的元素，然后重组来得到我们的参数矩阵 θ(1) θ(2) θ(3) 。接着我们用参数矩阵来执行前向传播和反向传播来计算出我们的代价函数的J(θ)和偏导数的值当然我们首先得到的都是矩阵。最后，我可以取出这些导数值，然后展开它们，让它们保持和我展开的θ值同样的顺序并且返回就可以了。

以上就是矩阵展开的相关内容，相信你已经有所掌握了。

梯度检测

在之前的BLOG中，我们一同学习了如何进行前向传播和后向传播，来计算我们的代价函数和偏导数。但后向传播有很多复杂细节，如果细节出现问题，就会导致一些BUG。如果这时我们用梯度下降来计算，我们可能会发现表面上它可以工作，即虽然每次迭代都在下降，但是可能最后得到的结果实际上有很大的误差。所以怎么办呢？有一个想法叫梯度检验 ，即Gradient Checking， 它能减少这种错误的概率。

那我们的梯度检测是如何实现的呢？假设我们有一个关于theta的函数 H 我现在有它的一个值，假设这个值 θ 是实数：

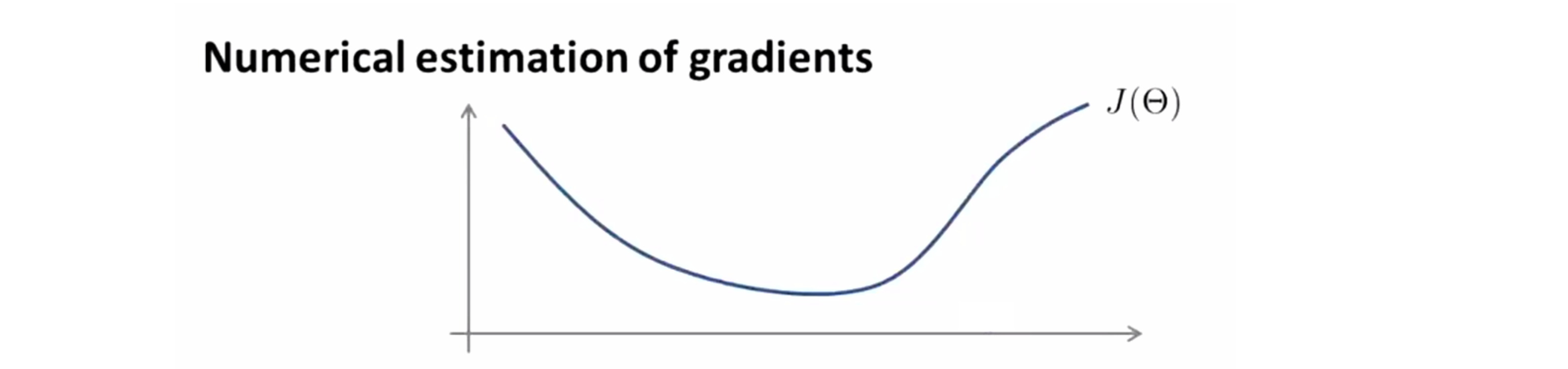
我们假设最后现在我们下降到点 θ ，我们现在来验证这个点的在反向传播中计算的导数值和真实情况是否一致。为了起到验证作用，在这里我们我们不采用数值的方法计算倒数，而是直接用下面这种方法来计算：

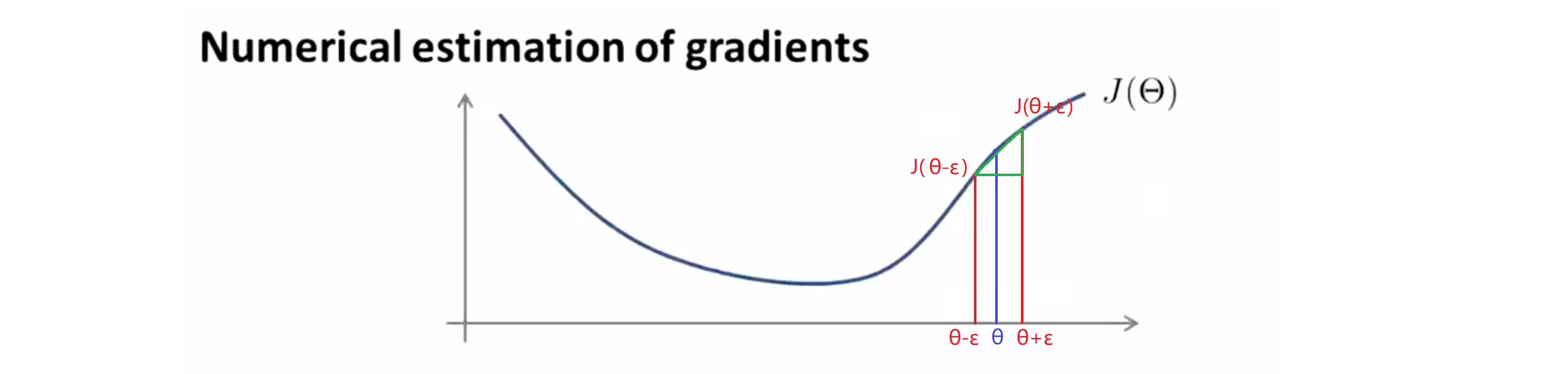
这里我们对于 θ 这个点，取 θ - ε 和 θ + ε 两点，然后把他们链接起来就得到了一条绿色的直线，我用这个绿色的斜线来近似我的导数。当 ε 很小的时候，我们就可以近似地认为这条绿色的斜线就是我们。而这里的绿线的垂直高度除以水平宽度就是我们绿线的斜率，具体来说k = (J(θ + ε) - J(θ - ε)) / 2。而当我们用 Octave 计算近似梯度时候， 我们用的是下面这个公式：

gradApprox = (J(theta + EPSILON) – J(theta – EPSILON)) / (2*EPSILON)

以上是我们的参数 θ 是一个实数时的梯度检查操作方法，下面我们来看看 θ 是一个向量的情况。其实经过数学的推导，其近似公式就如下：

具体的推导过程我就不展示了，感兴趣的同学可以自行推导。如果我们用 Octave 中来计算，过程就大致如下：

for i = 1:n,
    thetaPlus = theta;
    thetaPlus(i) = thetaPlus(i) + EPSILON;
    thetaMinus = theta;
    thetaMinus(i) = thetaMinus(i) – EPSILON;
    gradApprox(i) = (J(thetaPlus) – J(thetaMinus)) / (2*EPSILON);
end;

在上面这段程序中， n 是我们参数的个数。在我们的近似计算后，我们可以写一个循环来检验我们的这个近似计算的结果是不是等于我们神经网络的计算结果，即反向传播算法计算的梯度结果，即去判断是否有gradApprox ≈ DVec。Dvec 就是我们反向传播得到的导数，gradApprox就是我们近似计算的结果。

以上就是梯度检测的具体内容，下面让我们来总结一下。其实我们的总体工作就分为四步：

1.使用反向传播来计算，计算出梯度值DVec。
2.我们使用近似算法计算，计算出梯度值gradApprox。
3.将我们近似计算得到的梯度值与反向传播的计算结果对比检验。
4.最后也是最重要的步骤，就是在我们正式开始学习算法之前，关掉我们的梯度检验。原因是这个近似计算的计算过程，实际上时间代价更高，复杂度也很高，不是一个很好的计算导数的方法。一旦我们检验证明反向传播算法没有错误，我们就要把梯度检验关掉。

随机初始化

当我们使用梯度下降算法或者其他高级的优化算法时，我们需要设置参数 Θ 的初始值。对于高级的优化算法，我们需要传入一个初始值 initialTheta：

optTheta = fminunc(@costFunction, initialTheta, options)

在梯度下降中，我们也需要有一个初始的参数 θ， 之后再一步步通过梯度下降走到山坡底部。那我们怎么设置参数 theta的初始值呢？能不能就全部是零呢？全部是零在之前的逻辑回归里可行，但在神经网络中是不可行的。

假设我们现在有这么一个网络，假设全部参数为0：

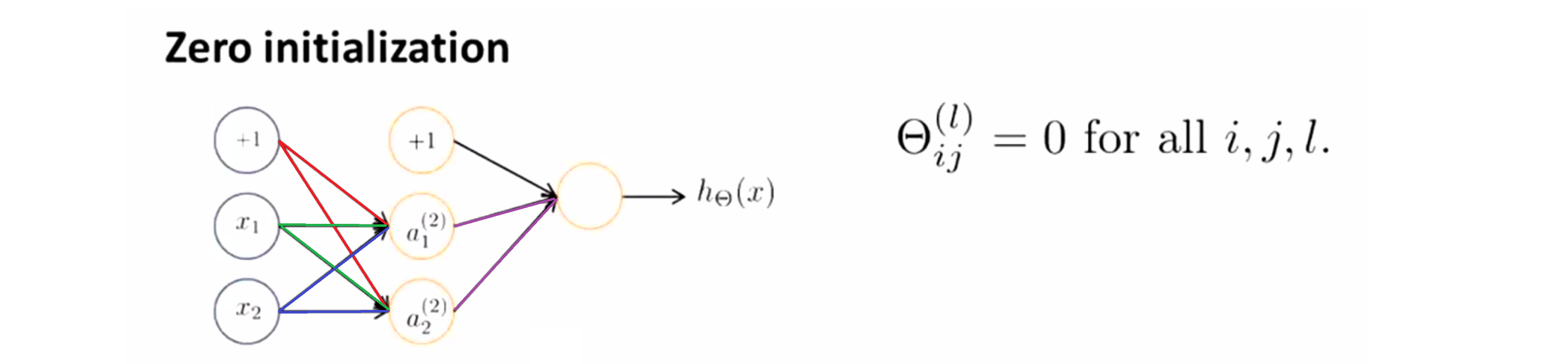
如果我们这么做，那蓝色线的权值，红色线的权值和绿色线的权值全是0。所以对于 a(2)1 和 a(2)2 这两个隐藏层单元，会有a(2)1 = a(2)2；此外，因为这输出边也就是紫色边的权值也是0，所以我们可以发现他们的反向传播得到的误差值也一样即δ(2)1 = δ(2)2，所以隐藏层计算出来的偏导数也是一样的。所以这就导致了每次更新的时候，通过计算梯度，隐藏层的两个元素的值会相等。所有我们的隐层的结果都一样，就导致了神经元的冗余，这就使得你的神经网络性能下降，无法进行更有意义的功能。，所以我们需要随机初始化。

具体来说，我们之前看到的问题叫做对称现象。所以我们的随机初始化要做的就是打破对称，但初始区间就是在特定范围内，比如[-ε， +ε]。下面是在Octave中生成特定区间随机数的代码：

Theta1 = rand(10,11)*(2*INIT_EPSILON) - INIT_EPSILON;
Theta2 = rand(1,11)*(2*INIT_EPSILON) - INIT_EPSILON;

通过这段代码，我们生成的矩阵中的元素都在epsilon到+epsilon范围当中，然后你再使用前向传播和反向传播，就能打破我们的对称化问题，真正让神经网络发挥作用。

结语

通过这篇BLOG，相信你已经掌握了这三个神经网络的相关技巧，赶快去实现它们吧！最后希望你喜欢这篇BLOG！