在我这只蒟蒻在瑟瑟发抖地刷二分图的题目时，惊讶地发现，居然有博弈论用二分图来解答！(大佬轻喷orz)这篇BLOG就让我们来一起了解一下如何用二分图来解决一些博弈论的题目把！

一类博弈论问题

首先我们要明白，二分图并不能解决所有博弈论的问题。这篇BLOG我们要讨论的一类博弈问题，是基于以下条件：

1.博弈者人数为两人，双方轮流进行决策。
2.博弈状态（对应点）可分为两类（状态空间可分为两个集合），对应二分图两边（X集和Y集）。任意合法的决策（对应边）使状态从一类跳转到另一类。（正是由于这个性质使得问题可以用二分图描述）
3.不可以转移至已访问的状态。（不可重复访问点）
4.无法转移者判负。

什么看的不是很懂，没事我们来看看下面这两种经典模式。

轮流放棋子问题

题目样式:
一个n*n的方格，A，B交替摆放棋子，A先从最角落一个方格内放置，下一个人放棋子只能在当前位置的相邻位置（上下左右）放置，放过的格子就不能再放了，如果没得放了就算输了。

我们可以把问题一般化，考虑一个任意形状的棋盘（可以奇形怪状，但要求联通），从某一个位置开始放置。将棋盘黑白染色（像国际象棋棋盘那样），则状态可分为两类（棋子在白格与棋子在黑格）。把每个格子和周围4个相邻格连边（边界的格可能只有2或3个相邻格），则黑格只与白格连边，白格只与黑格连边，每次转移（放置）肯定是从黑到白或从白到黑，因此图是一个二分图。

具体如何黑白染色，其实是有一个非常简单的方法的，我们可以对于任意一个格子，我们假设它的坐标为(x,y)，那么当 (x+y)为偶数时，染成白色，(x+y)为奇数时，染成黑色，这样就可以保证任意一个格子与其相邻的格子都异色。

在黑白染色后，我们把相邻的点进行连边，很显然，连出来的图是一个二分图，左边的点全部都是白色，右边的点全部都是黑色。

同样的，就算给出来的棋盘已经不是一个方形的，而是：
1.png

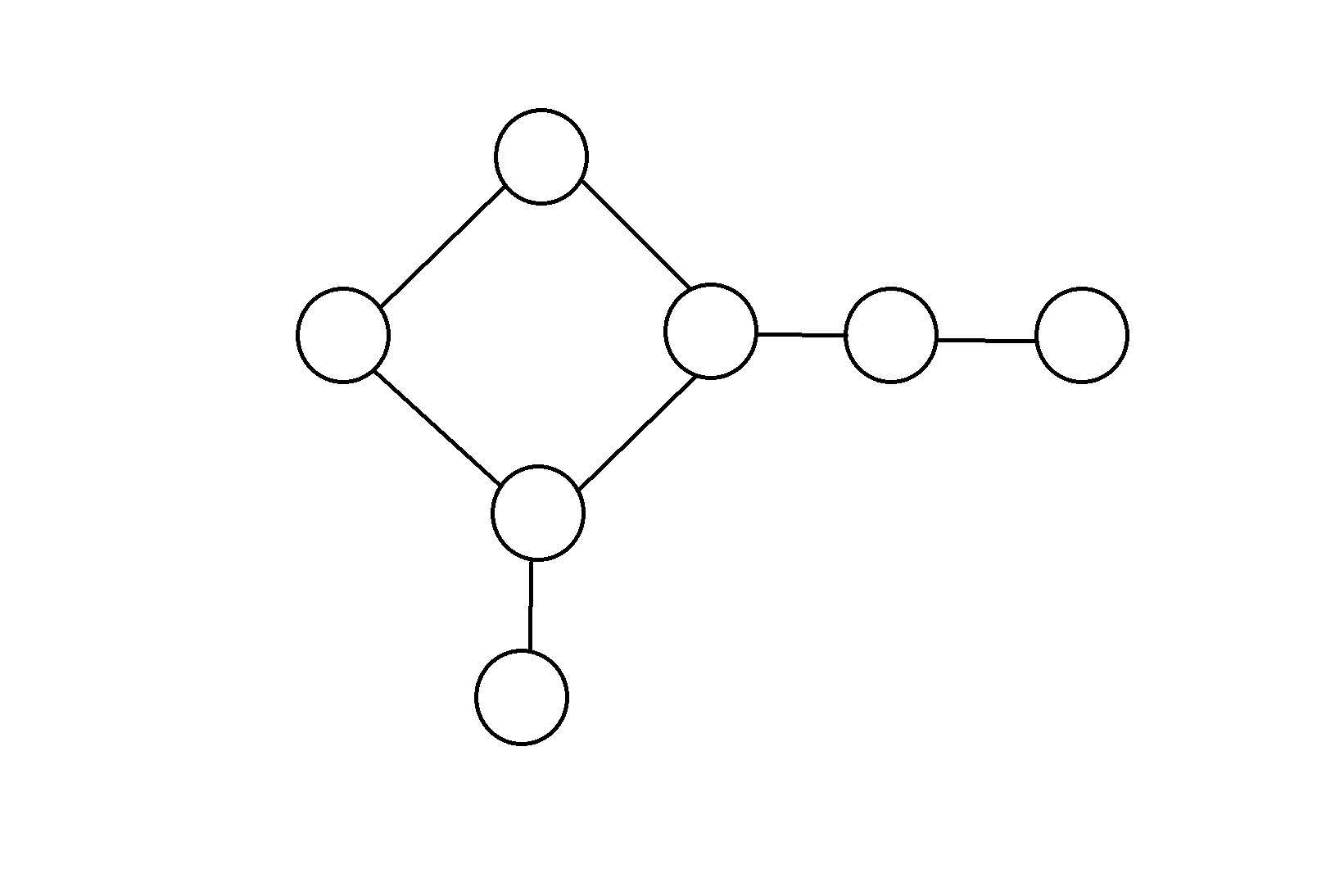
这样一种奇奇怪怪的样子，也是可以黑白染色的，我们可以从任一个节点出发(这里从紫色箭头所指向的点开始)，先令他为白色，将与他相临的未染色的点染成黑色，放到队列里，再对队列中的队列，访问它的每一个相邻点，若未染色则染成黑色，放到队列里……以此类推，最后就就能完成染色了。

2.png

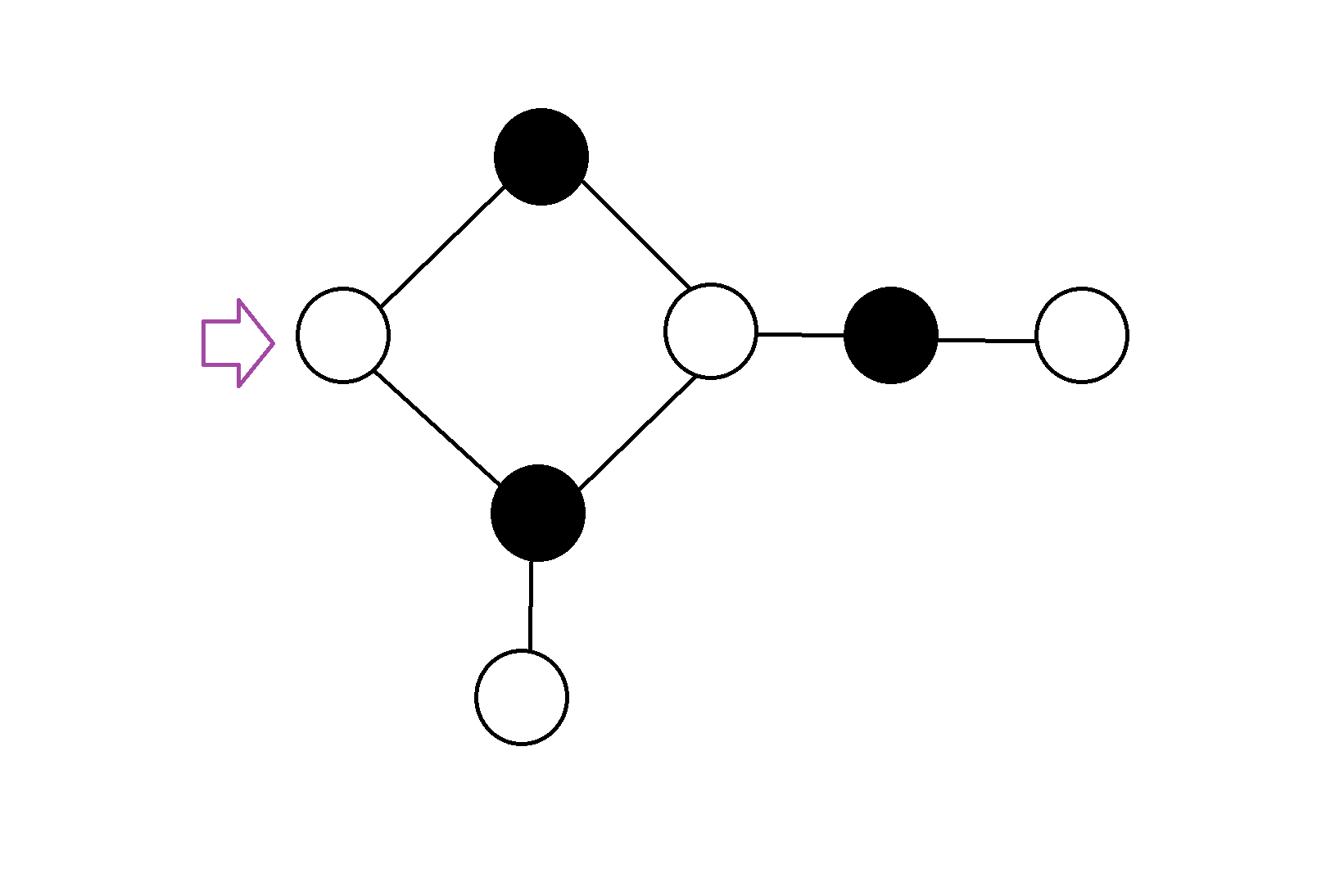
现在考虑对于先手，怎么样才是必胜的？

我们直接对构造出来的二分图进行分析，加入我们黑白染色后，我们构造出了下面这个二分图：

3.png

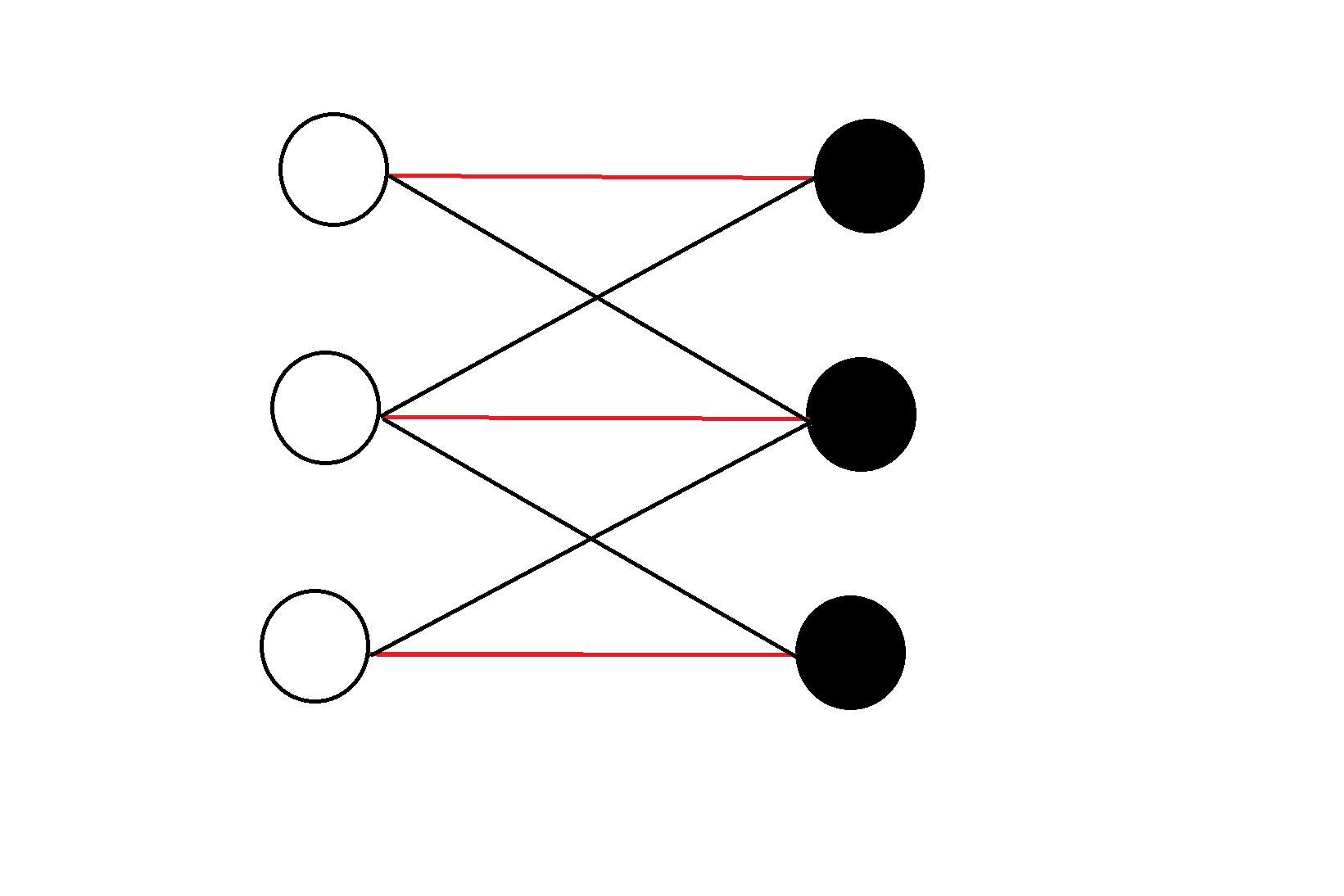
很明显，此时的二分图已经达到了完美匹配。那如果你是先手，那就很高兴的恭喜你，你GG了！不论你放在哪个点，都有与你相连的匹配边(即红边)连向另一颜色的点。对面沿着红线跳完后，你只能再从对面选好的点沿着黑线跳到一个之前没有选过的本来颜色的点，但对面有一定能沿着那个点的红线跳到另一半……最后对面跳完了，你发现没有点可以跳了，你GG，如下图：

5.png

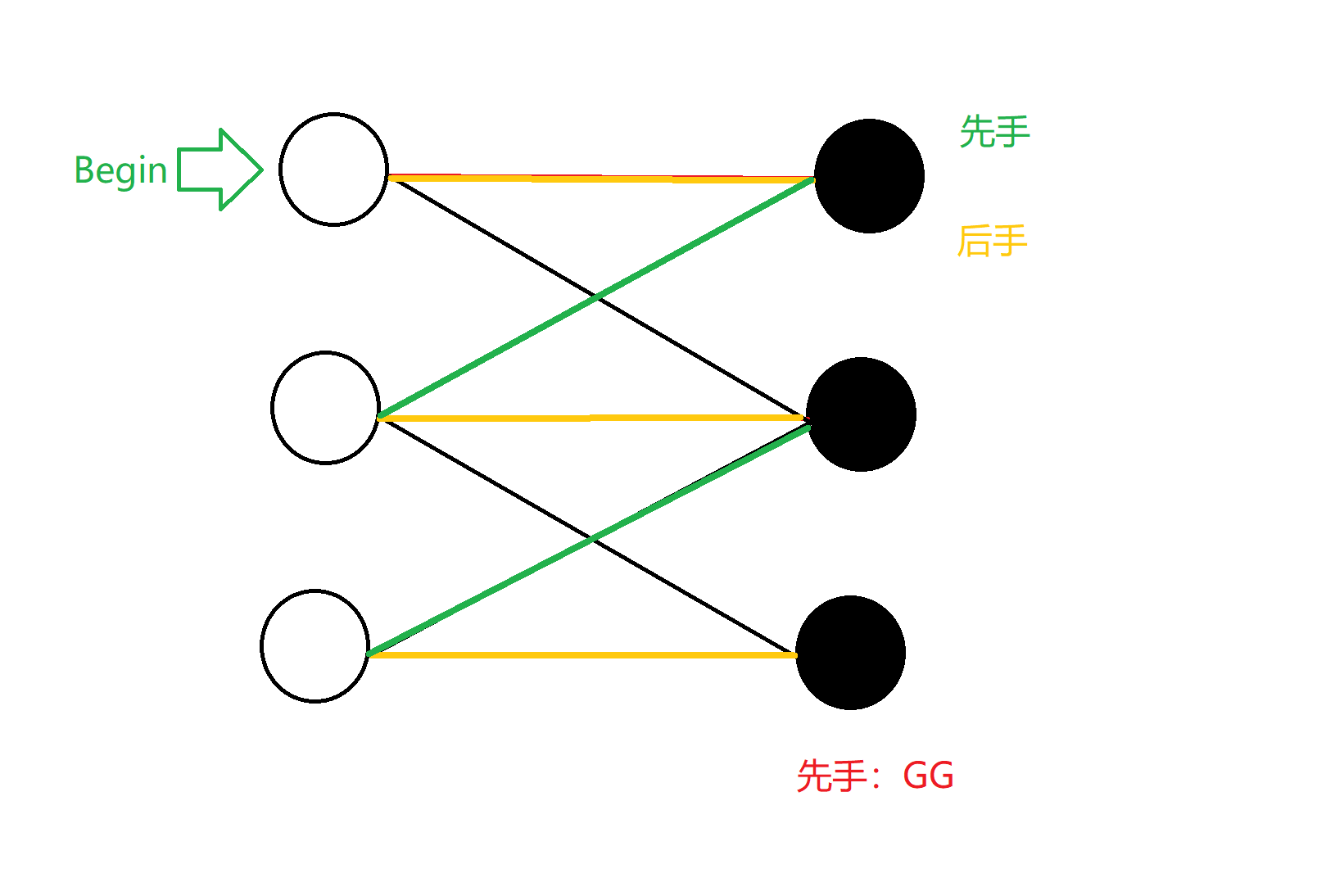
但是若此时二分图不是完美匹配：

4.png

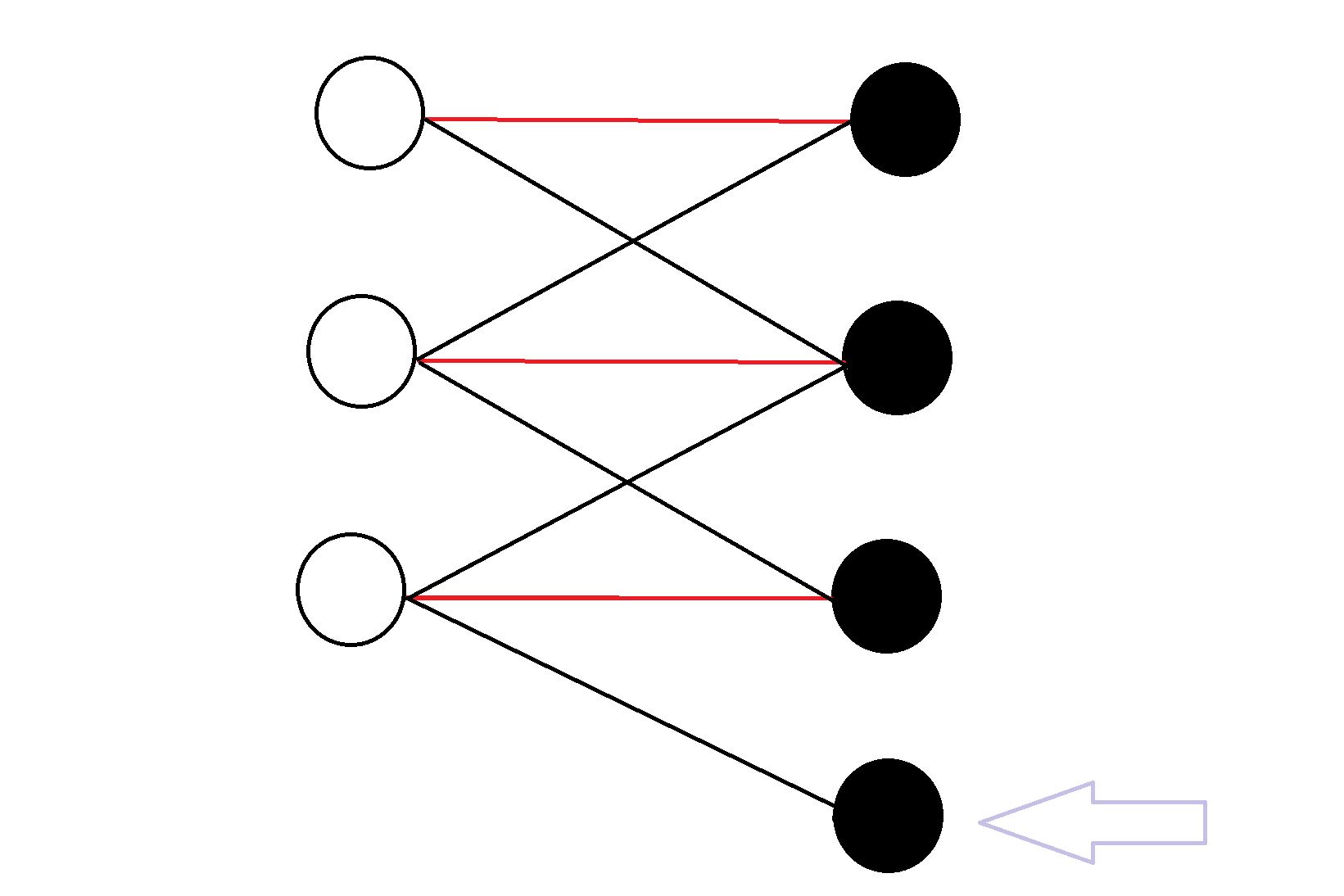
那作为先手，你就很开心了，你只要将棋子放在任意一个非匹配点就好啦！因为这个非匹配点的连边都是连向匹配点(若还有连向非匹配点，则代表二分图还有更大的匹配，与原命题相违背，故不可能)，则对手在下一步只能作为第一步跳入匹配点中，那你就很简单了，你只要按照上面那种情况，对手的策略沿着匹配边一直跳就好了。

轮流移动棋子问题

题目样式:
在n*m的矩阵上有两个相同的棋子，有些格子是不能走的。现在两个人开始轮流对棋子操作：每次只能将其中一颗棋子向四个方向移动一格，不能移出边界，谁将两个棋子重合谁将胜利；同时移动时不能出现前面移动时出现过的局面，不能移动的就算是失败了。

这就是比较难的二分图解决博弈论的题目了。还是考虑一个一般的棋盘，同样黑白染色。如果先手面临两个棋子相邻的状况那么显然他就胜利了，因此我们把这个状态视为非法，即不允许有玩家转移到该状态（否则他一定输）。

因此，现在考虑所有两个棋子不相邻的可能状态。两个棋子的所有状态看作点，可分为两类（棋子在同色/异色格），能够转移之间的状态连边，则图是一个二分图。无法继续转移则判负。

现在问题变为从二分图指定起点开始轮流移动，不可重复访问点，无法移动判负。

不妨设起点在二分图的X集中，那么先手只能从X集移动到Y集，后手只能从Y集移动到X集。一次游戏过程对应一条路径 。若最后停留在X集且无法移动则先手负，停留在Y集则后手负。

考虑该二分图的某个最大匹配。（注意可能存在多个匹配相同的最大匹配）

若起点s∈X不属于该最大匹配。则先手所转移到的点y∈Y一定属于最大匹配（否则s-y是一个匹配，与最大匹配矛盾）。后手沿着最大匹配的边走即可，终点t（指无法从t再走一步）一定不可能在Y集中（否则，若t在Y集中，s-...-t为一增广路，与最大匹配矛盾）。因此先手必败，后手必胜。

若起点s∈X属于该最大匹配。则将s从图中删除，再求图的最大匹配。若最大匹配数不变，则s还是不属于某最大匹配，先手必败。否则该图的任意最大匹配都包含s，则先手沿着最大匹配的边走即可，根据上面的分析，先手必胜。

我们再来回头看上面的第一个例题，假设先手从某个虚拟起点s移动到角落。若n为偶数，显然最大匹配数为n^2/2，且可以找到一最大匹配使得s不属于最大匹配，则先手必败；若n为奇数，则最大匹配数为(n^2+1)/2（包含s的图可以用1x2的黑白方块密铺），且s一定属于最大匹配，则先手必胜。

经典例题

刚刚我们一起学习了两种经典模型，现在我们来看看OI战场上考过的经典例题吧！

【luogu P4055】 [JSOI2009]游戏
题目描述
小AA和小YY得到了《喜羊羊和灰太狼》的电影票，都很想去观看，但是电影票只有一张，于是他们用智力游戏决定胜负，赢得游戏的人可以获得电影票。

在N*M的迷宫中有一个棋子，小AA首先任意选择棋子放置的位置。然后，小YY和小AA轮流将棋子移动到相邻的格子里。游戏的规则规定，在一次游戏中，同一个格子不能进入两次，且不能将棋子移动到某些格子中去。当玩家无法继续移动棋子时，游戏结束，最后一个移动棋子的玩家赢得了游戏。

例如下图所示的迷宫，迷宫中”.”表示棋子可以经过的格子，而”#”表示棋子不可以经过的格子：
6.png

若小AA将棋子放置在(1,1)，则小 AA 则无论如何都无法赢得游戏。

而若小AA将棋子放置在(3,2)或(2,3)，则小AA能够赢得游戏。例如，小AA将棋子放置在(3,2)，小YY只能将它移动到(2,2)，此时小AA再将棋子移动到(2,3)，就赢得了游戏。

小AA和小YY都是绝顶聪明的小朋友，且从不失误。小AA到底能不能赢得这场游戏，从而得到珍贵的电影票呢？

输入输出格式
输入格式：
输入数据首先输入两个整数 N,M，表示了迷宫的边长。接下来 N 行，每行 M 个字符，描述了迷宫。

输出格式：
若小 AA 能够赢得游戏，则输出一行"WIN"，然后输出所有可以赢得游戏的起始位置，按行优先顺序输出，每行一个。

否则输出一行"LOSE"（不包含引号）。

输入输出样例
输入样例#1：
3 3
6.png
输出样例#1：
WIN
2 3
3 2
说明
对30%的数据，有1<=n,m<=5
对100%的数据，有1<=n,m<=100

很明显，看到题目，如果你已经理解了上面的模型，那么黑白染色然后求二分图最大匹配判断与总点数大小得出Win还是Lose你肯定是知道了。剩下的问题就是，当我先手下在一个非匹配点上，就可以赢，但是最大匹配不止又一种，所以我们需要判断是否在最大匹配中，需要寻找交错路，什么是交错路呢？就我们先跑一遍最大匹配，然后从左右两边的每一个非匹配点出发，查找有没有能连向另一边的x点，且x又能通过匹配边连向这一边的一个“转折路”，如果有，就把最后走到的这边的这个匹配点设置为非匹配点就好了。这是为什么呢？我们想我们找到一个转折边意味着什么？意味着我们如果在匹配的时候选择转折边的非匹配边，而丢弃匹配边，答案是不变的，故转折边的末尾可以不出现在最大匹配上。即如果走到非最大匹配的点上，那么就相当于找到一条交错路可以替换，反而让非最大匹配换到了最大匹配中。

这样求出来的就是一定不在最大匹配中的点了。

贴上代码：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std;
char s[220];
bool vis[110000],ans[110000],mark[220][220];
int cnt,h[110000],match[110000],n,m,nm,num,ret,q[110000];
int dx[4] = {0, 1, -1, 0};
int dy[4] = {-1, 0, 0, 1};
struct edge{
    int v, nxt;
}e[220000];
inline void add(int u,int v){
    e[++num].v = v, e[num].nxt = h[u], h[u] = num; 
    e[++num].v = u, e[num].nxt = h[v], h[v] = num;
}
bool find(int u)
{
    for(int i = h[u]; i; i = e[i].nxt)
         if(!vis[e[i].v])
         {
             int v = e[i].v;
             vis[v] = true;
             if(!match[v] || find(match[v])) return match[v] = u;
         }
     return false;
}
void dfs(int u)
{  
    ans[u] = true;  
    for(int i = h[u]; i; i = e[i].nxt)
    {
        int v = e[i].v;  
        if(match[v] && !ans[match[v]]) dfs(match[v]);   
    }  
}
int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; ++i)
    {
        scanf("%s", s + 1);
        for(int j = 1; j <= m; ++j)
        if(s[j] == '.') mark[i][j] = true;
    }
    for(int i = 1; i <= n; ++i)
    for(int j = 1; j <= m; ++j)
    if(mark[i][j])
    for(int k = 0; k < 4; ++k)
    if(mark[i + dx[k]][j + dy[k]]) add((i - 1) * m + j, (i + dx[k] - 1) * m + j + dy[k] + n * m);

    for(int i = 1; i <= n; ++i) 
    for(int j = 1; j <= m; ++j)
    if(mark[i][j])
    {
        if(!find((i - 1) * m + j)) q[++ret] = (i - 1) * m + j;
        memset(vis,0,sizeof(vis));
    }
    if(!ret) {puts("LOSE"); return 0;}
    puts("WIN");
    for(int i = 1; i <= ret; ++i) dfs(q[i]);
    for(int i = 1; i <= n; ++i)
    for(int j = 1; j <= m; ++j)
    if(ans[(i - 1) * m + j]) printf("%d %d\n", i, j);
}

结语

通过这篇BLOG，相信你已经理解了二分图如何解决一部分的博弈论的题目，那就快去谢谢题目吧。希望你喜欢这篇BLOG！

Last modification：July 23rd, 2018 at 02:04 pm
© 允许规范转载
If you think my article is useful to you, please feel free to appreciate