今天因为不会 伯努利-欧拉装错信封问题 被附近的大佬狠狠地嘲讽了一下,去学习了一下发现,这确实是个经典而有趣的问题,今天就让我们来分享一下这个问题吧!
什么是伯努利-欧拉装错信封问题
伯努利-欧拉装错信封问题 又称 错位重排问题,具体来说,就是——
我们有编号是1、2、…、n的n封信,装入编号为1、2、…、n的n个信封,要求每封信和信封的编号不同,即1不能装进1,2不能装进2,3不能装进3……问有多少种装法?
最开始看到这个问题时,第一反应就是通过组合数学进行计算。当然很多人第一反应都是,我们对于每一个i,前i-1个错位重排的可能排列一共有 a 种,那我对于每一种,,貌似都可以找除了最后一个位置进行插入(即除了红色箭头外的其他绿色箭头),又由于共有i-1个绿色箭头,所以共有i-1个插入位置,这样我插入的第i个数也满足错位重排了,如下:
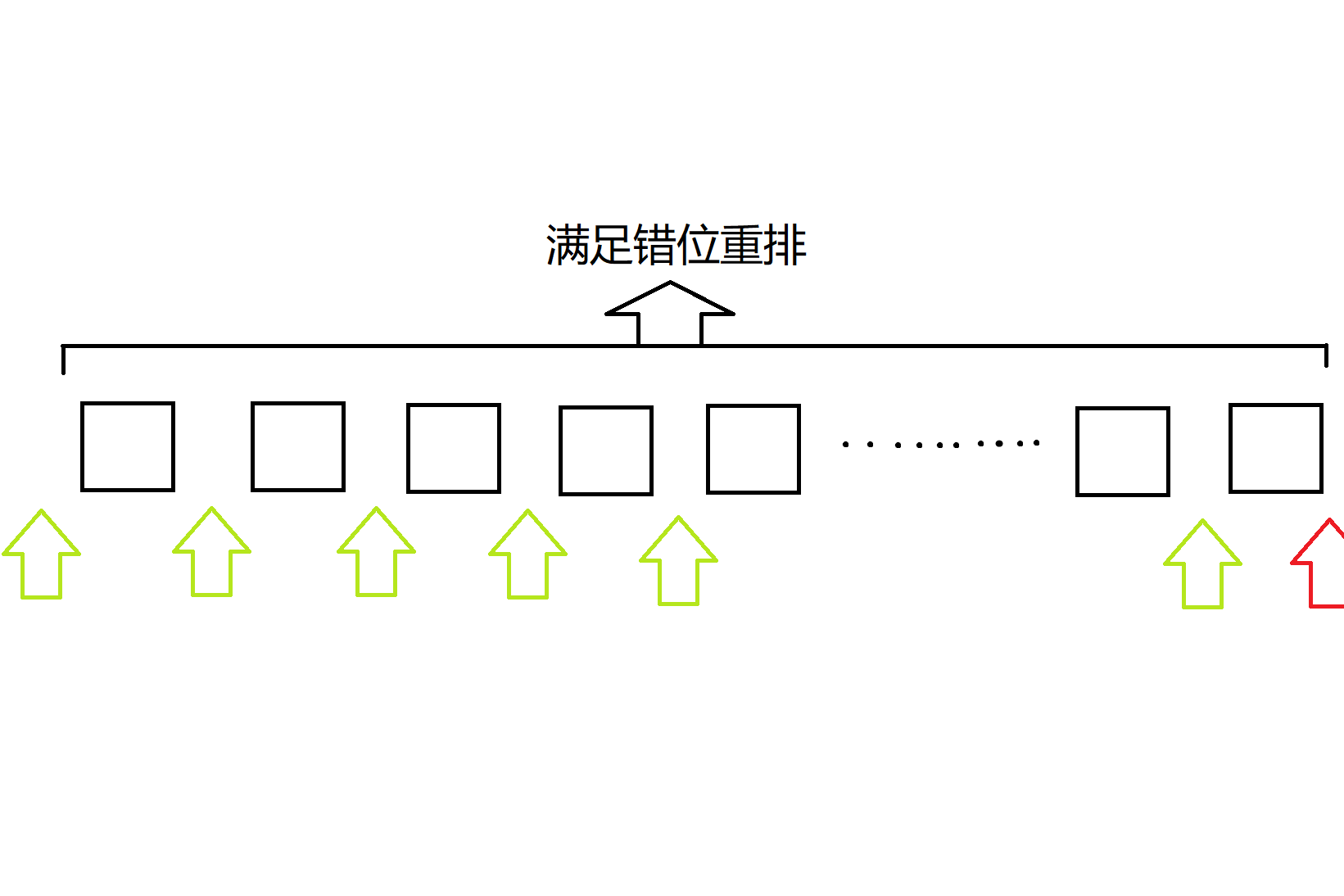
这样貌似算出来对于任意 i ,设F[i]为1-i的错位重排的数量,都有 F[i]=F[i-1]*(i-1)。
于是你很开心认为可以AC了,然后你就WA了,那么问题出现在哪里呢?其实,你上面推导的这一整个公式都是错的!
错误分析
我们来分析一下上面推导的公式为什么是错误的。我们在上面先对于处理第i封信放在哪里时,都会在每一个i-1的错位排列的基础上,在每一种i-1的错位排列的情况上把第i封信放在初最末尾外的其他位置。对这样对于第i封信来说,是已经满足错位排列了,但是你有没有想过,当你把一封信插在原来的[x,y]两封信之后,原来排在[y,i-1]的信都集体后移了一位,那移动后那段序列还符合错位排列吗?
不一定了,比如,我们要求4的错位排列数量,我们就先搞出一个3的错位排列:
然后我们准备把4插进来:
但按照原来的策略,我们完全可以把4插到最前面,这样4就满足错位排列了,但是2,3,1的后移导致了2,3都不符合错位排列了,这样就和我们的题目相违背了:
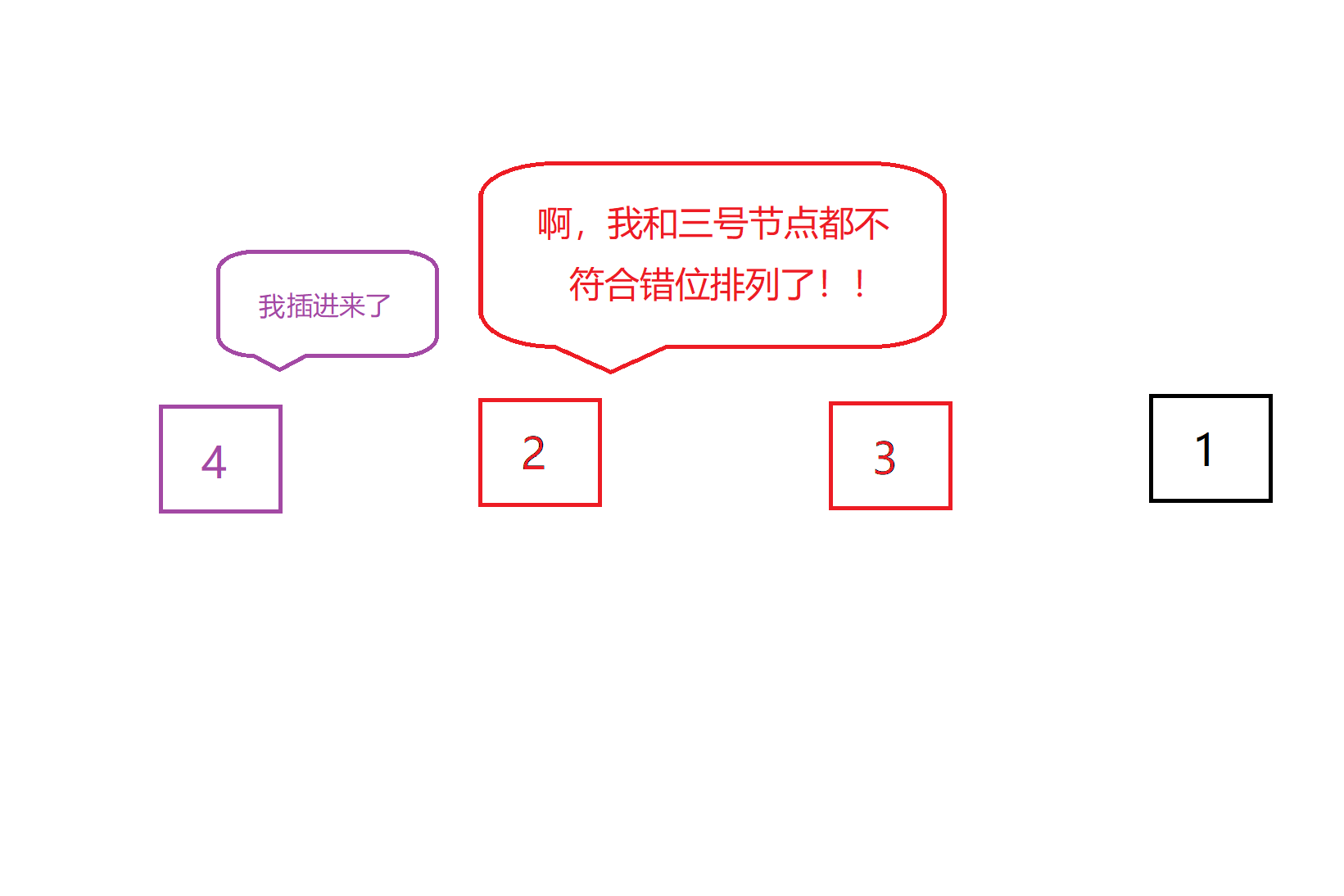
那我们不妨换一个思路想想。
正确的解法
我们设,设f[i]为i个数错位排序 (任意1<=i<=n a[i]!=i)通过常理我们知道:f[0]=1,f[1]=0;那么有
f[i]=(f[i-1]+f[i-2])*(i-1) (i>=2)
对这就是我们的结论了,但是这是为什么吗?不急我现在就告诉你证明的方法:
对于插入第i个元素,只有两种情况:
情况1:插入第i个元素时,前i-1个已经错位排好,则选择其中任意一个与第i个互换一定满足要求,选择方法共i-1种,前i-1位错排f[i-1]种,记f[i-1]*(i-1),如下图:
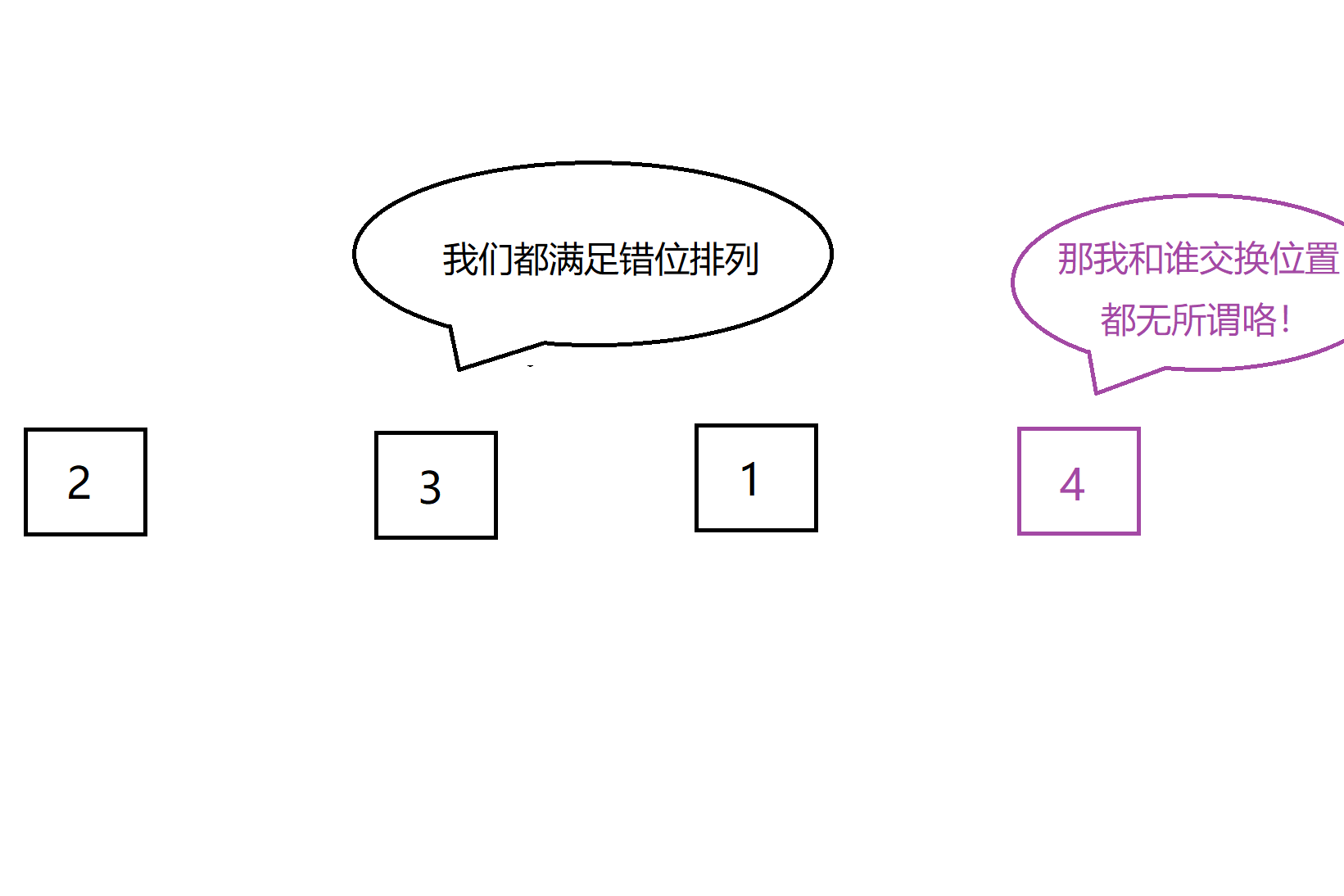
情况2:插入第i个元素时,前i-1个中恰有一个元素a[j]使得a[j]=j,即恰好只有一个元素不满足错位排列,其他i-2个错位排好,则将i与j交换,j在i-2位中的插入共i-1种,前i-2位错排f[i-2]种,记f[i-2]*(i-1),如下图:
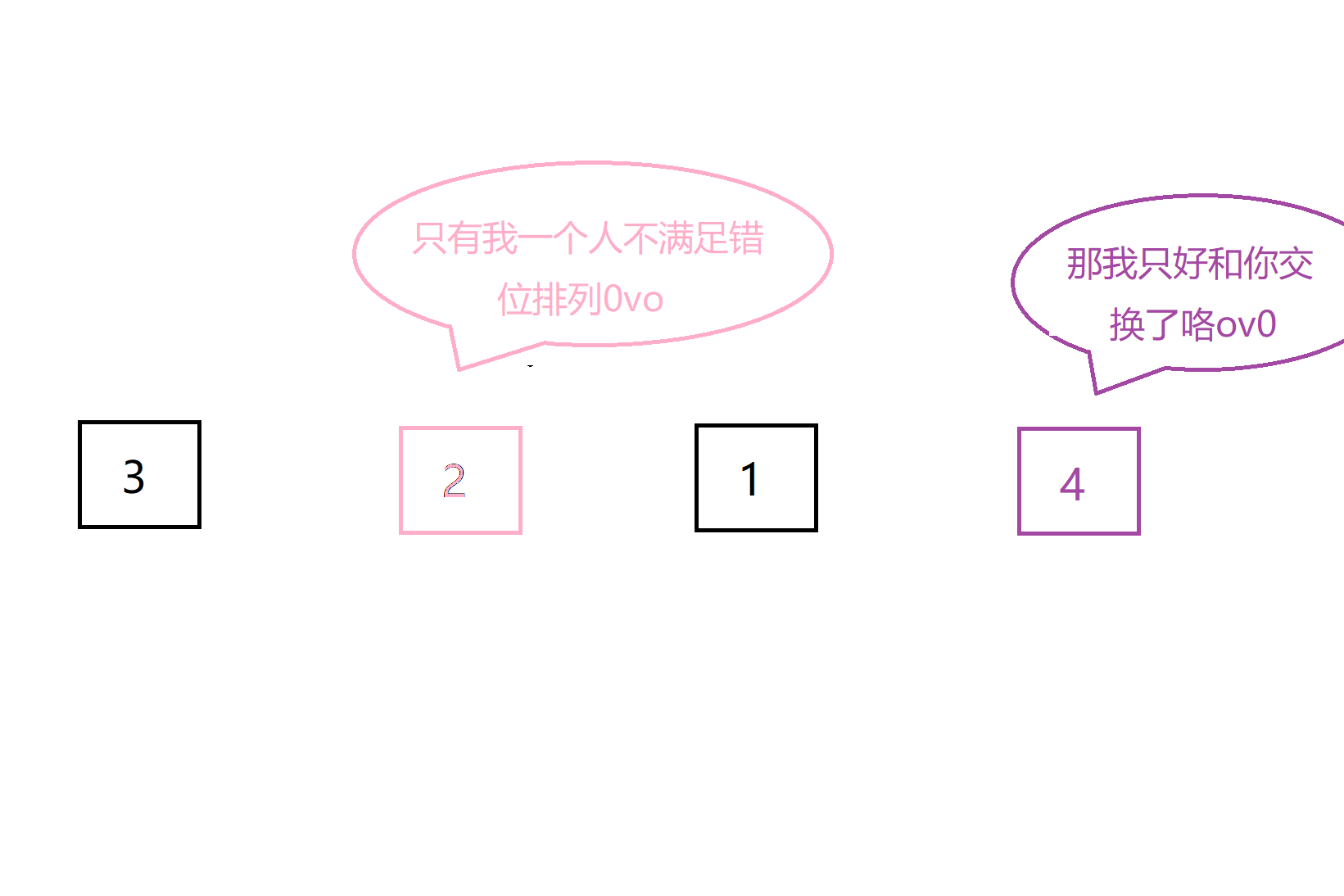
以上两种情况求和可得:
f[i]=(f[i-1]+f[i-2])*(i-1) (i>=2)
*来个通项公式

酱紫就得到我们的通项公式了!
*进一步讨论

经典例题
[luogu p3182]即[HAOI2016]放棋子
题目描述
给你一个N*N的矩阵,每行有一个障碍,数据保证任意两个障碍不在同一行,任意两个障碍不在同一列,要求你在这个矩阵上放N枚棋子(障碍的位置不能放棋子),要求你放N个棋子也满足每行只有一枚棋子,每列只有一枚棋子的限制,求有多少种方案。输入输出格式
输入格式:
第一行一个N,接下来一个N*N的矩阵。N<=200,0表示没有障碍,1表示有障碍,输入格式参考样例输出格式:
一个整数,即合法的方案数。输入输出样例
输入样例#1:
2
0 1
1 0
输出样例#1:
1
这一眼看过去就是伯努利-欧拉装错信封问题的裸题,由于开始时给的棋子在哪一行哪一列都不重要,因为求出来的答案都是一样的,所以我们只要把棋子i的、挪到第i行第i列就好了,剩下的问题就变成了,你有n个棋子,每列放一个,第i个棋子不能放在第i行,有多少种情况。这不是就是伯努利-欧拉装错信封问题吗?
注意n比较大要开高精度!!!附上模板:
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std;
int a[1100000],b[1100000],c[1100000];
int i,j,k,m,n,o,p,q,js,jl,jk,lena,lenb,lenc;
int my_max(int x,int y)
{
if(x>y)return(x);
else return(y);
}
int caozuo(int x)
{
lenc=lenb;
for(int i=1;i<=lenb;i++)
{
c[i]=a[i]+b[i];
c[i]=c[i]+c[i-1]/10;
c[i-1]=c[i-1]%10;
}
if(c[lenc]>=10)
{
c[lenc]-=10;
c[++lenc]=1;
}
for(int i=1;i<=lenc;i++)
{
c[i]=c[i]*(x-1);
c[i]=c[i]+c[i-1]/10;
c[i-1]=c[i-1]%10;
}
while(c[lenc]>=10)
{
c[++lenc]=c[lenc-1]/10;;
c[lenc-1]=c[lenc-1]%10;
}
lena=lenb;lenb=lenc;
while(c[lenc]==0)lenc--;
for(int i=1;i<=lena;i++)a[i]=b[i];
for(int i=1;i<=lenb;i++)b[i]=c[i];
}
int main()
{
scanf("%d",&n);
a[1]=0;b[1]=1;c[1]=1;
lena=1;lenb=1;lenc=1;
if(n==1)
{
printf("0");
exit (0);
}
if(n==2)
{
printf("1");
exit (0);
}
for(int i=3;i<=n;i++)
{
caozuo(i);
}
for(int i=lenc;i>=1;i--)printf("%d",c[i]);
return 0;
}结语
在这篇BLOG中,我们学习了非常经典的伯努利-欧拉装错信封问题,注释*的框体均参考文献-武汉大学刘学智的论文《关于装错信封的讨论》。希望你能切实掌握这种算法,不要像我一样被大佬们嘲笑。希望你喜欢这篇BLOG!
我要被大佬嘲笑了(ó﹏ò。)
我想问问,为什么没有情况3,恰有2个元素不满足错位排列,
哦我好像知道了
QwQ
QwQ