在去年银川站的比赛中，我们就因为一道四边形不等式优化动态规划的题目与金牌失之交臂。四边形不等式作为动态规划的常用优化技巧，在竞赛中运用极多。下面就让我们一起来学习这个神奇的技巧吧！

[NC 51244] Post office

题目描述

在一个一维坐标轴上有 $v(1 \le v \le 300)$ 个村庄，要建 $p(1 \le p \le 30)$ 个邮局，每个邮局都在村庄上。每个村庄都会去最近的邮局办事，求最小的距离和。

解题思路

我们先考虑最简单的做法，我们首先先将村庄坐标排序，设 $f[i][j]$ 为前 $j$ 个村庄建 $i$ 个邮局的最小距离和。那么 $f[i][j] = min(f[i - 1][k] + w[k + 1][j])$。其中 $w[k + 1][j]$ 表示在第 $k + 1$ 个村庄到第 $j$ 个村庄之间建一个邮局，并且第 $k + 1$ 个村庄到第 $j$ 个村庄都到这个邮局的最小距离和。那对于这第 $k + 1$ 个村庄到第 $j$ 个村庄，一定是在这些村庄的最中间的村庄上建邮局。这样的话我们预处理出 $w$ 数组，时间复杂度就是 $O(v^3)$，是可以过的，但是其实 $v=1000, p=1000$ 也是可以做的。

我们首先有个猜想，就是我们的 $j$ 变成 $j + 1$ 的时候，我们的转移点 $k$ 只会往右移，不会往左移，这个看起来还挺显然的，我们多一个点所以我们的邮局要往右多建一建。还有一个单调性就是当我们的 $i$ 变成 $i+1$ 的时候，我们的 $k$ 也就是最后一个邮局负责的左端点位置只会向右移动，不会往左移动，因为多一个邮局整体肯定要更匀称，也就是最后一个邮局负责的区域肯定是更小一点也就是左端点更靠右边的。

比赛的时候虽然可能不会证明单调性，但是单调队列一写就过了。但实际上我们现在作为练习，还是要证明一下的。

第一步-证明w为凸

第一步证明 $w$ 为凸，即满足 $w[i][j] + w[i + 1][j + 1] \le w[i + 1][j] + w[i][j + 1]$。

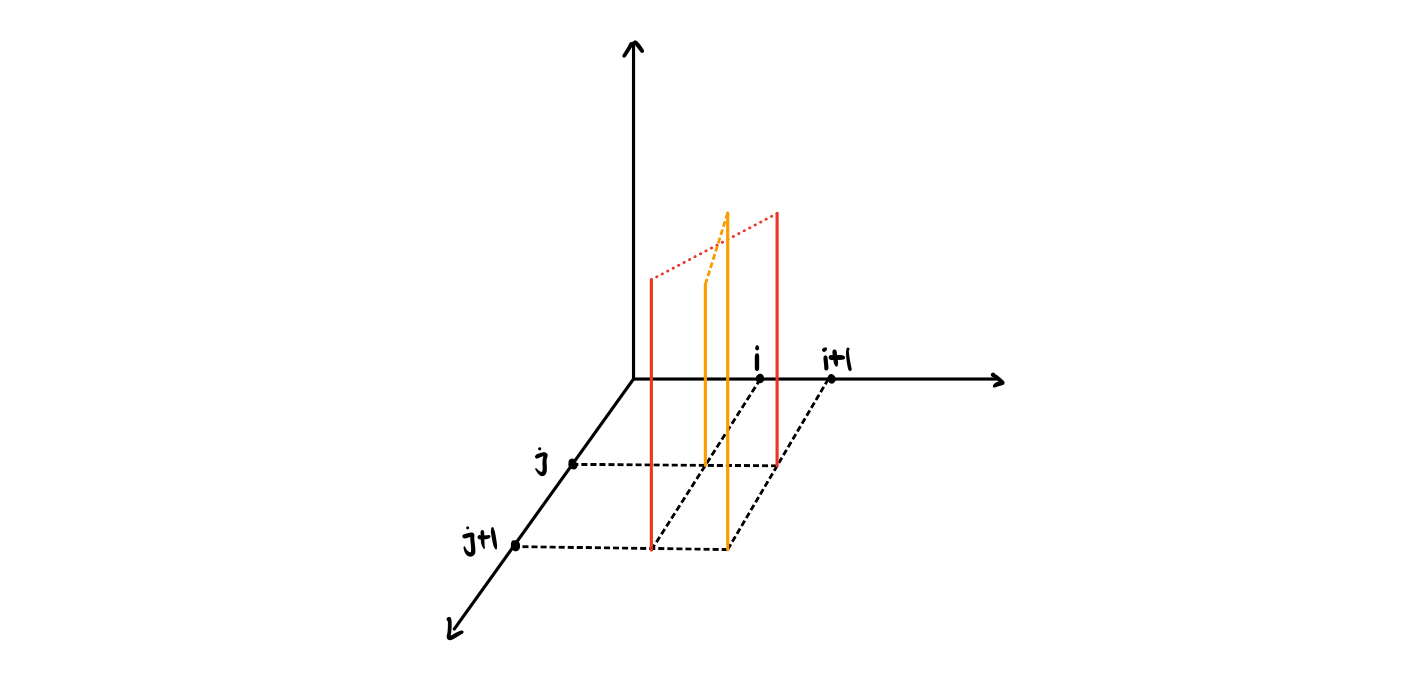
就是右边的连线中点高于左边的。所以整体就是类似于一个碗，有一个下凹面的存在，我们一般上凸和下凸都叫凸，所以就说有凸性。我们下面来证明。

我们设第 $i$ 个点到第 $j$ 个点的中点是第 $x + \Delta_0$ 个点，设第 $i + 1$ 个点到第 $j$ 个点的中点是第 $x + \Delta_1$ 个点，设第 $i$ 个点到第 $j + 1$ 个点的中点是第 $x + \Delta_2$ 个点，设第 $i + 1$ 个点到第 $j + 1$ 个点的中点是第 $x + \Delta_3$ 个点。

我们考虑 $i$ 到 $j$ 中每一个点到第 $x + \Delta_0$ 个点的距离和一定小于等于到其他点的距离和，所以 $\sum dis(o, x + \Delta_0) \le \sum dis(o, x + \Delta_i)$，其中 $o$ 为 $i$ 到 $j$ 中的点，$i$ 的取值为 $1, 2, 3$。

我们来展开式子，得到，其中 $P_i$ 为第 $i$ 个点的坐标：
$$
P_{x + \Delta_0} - P_i + P_{x + \Delta_0} - P_{i + 1} + \dots + P_{x + \Delta_0} - P_{x + \Delta_0} + \dots + P_{j - 1} - P_{x + \Delta_0} + P_j - P_{x + \Delta_0} \le P_{x + \Delta_i} - P_i + P_{x + \Delta_i} - P_{i + 1} + \dots + P_{x + \Delta_i} - P_{x + \Delta_i} + \dots + P_{j - 1} - P_{x + \Delta_i} + P_j - P_{x + \Delta_i}
$$
我们可以把 $P_i$ 到 $P_j$ 全部约掉，所以我们左边化简有：
$$
(x + \Delta_0 - i + 1) P_{x + \Delta_0} - (j - (x + \Delta_0)) P_{x + \Delta_0} = (2(x + \Delta_0) - i - j + 1) P_{x + \Delta_0}
$$
同理右边化简有：
$$
(x + \Delta_i - i + 1) P_{x + \Delta_i} - (j - (x + \Delta_i)) P_{x + \Delta_i} =(2(x + \Delta_i) - i - j + 1) P_{x + \Delta_i}
$$
所以：
$$
① (2(x + \Delta_0) - i - j + 1) P_{x + \Delta_0} \le (2(x + \Delta_i) - i - j + 1) P_{x + \Delta_i}
$$
考虑 $[i+1 \sim j]$ 就同理有：
$$
② (2(x + \Delta_1) - i - j) P_{x + \Delta_1} \le (2(x + \Delta_i) - i - j) P_{x + \Delta_i}
$$
考虑 $[i \sim j + 1]$ 就同理有：
$$
③(2(x + \Delta_2) - i - j) P_{x + \Delta_2} \le (2(x + \Delta_i) - i - j) P_{x + \Delta_i}
$$
考虑 $[i + 1 \sim j + 1]$ 就同理有：
$$
④(2(x + \Delta_3) - i - j - 1) P_{x + \Delta_3} \le (2(x + \Delta_i) - i - j - 1) P_{x + \Delta_i}
$$
这是我们写出 $w[i][j], w[i + 1][j + 1], w[i + 1][j], w[i][j + 1]$ 有：

$$
(1)w[i][j] = P_{x + \Delta_0} - P_i + P_{x + \Delta_0} - P_{i + 1} + \dots + P_{x + \Delta_0} - P_{x + \Delta_0} + \dots + P_{j - 1} - P_{x + \Delta_0} + P_j - P_{x + \Delta_0}
$$

$$
(2)w[i + 1][j + 1] = P_{x + \Delta_3} - P_{i + 1} + P_{x + \Delta_3} - P_{i + 2} + \dots + P_{x + \Delta_3} - P_{x + \Delta_3} + \dots + P_{j} - P_{x + \Delta_3} + P_{j + 1} - P_{x + \Delta_3}
$$

$$
(3)w[i + 1][j] = P_{x + \Delta_1} - P_{i + 1} + P_{x + \Delta_1} - P_{i + 2} + \dots + P_{x + \Delta_1} - P_{x + \Delta_1} + \dots + P_{j} - P_{x + \Delta_1}
$$

$$
(4)w[i][j + 1] = P_{x + \Delta_2} - P_{i} + P_{x + \Delta_2} - P_{i + 1} + \dots + P_{x + \Delta_2} - P_{x + \Delta_2} + \dots + P_{j} - P_{x + \Delta_2} + P_{j + 1} - P_{x + \Delta_2}
$$

计算 $(1)+(2)-(3)-(4)$ ，其中每个式子的偶数项都恰好被约掉了，所以结果为：
$$
(2(x + \Delta_1) - i - j + 1)P_{x + \Delta_0} + (2(x + \Delta_3) - i - j - 1)P_{x + \Delta_3} - (2(x + \Delta_2) - i - j)P_{x + \Delta_2} - (2(x + \Delta_1) - i - j)P_{x + \Delta_1}
$$
那我们把负号带入式子其实就是下面四个式子相加：
$$
[1] \space +(2(x + \Delta_0) - i - j + 1)P_{x + \Delta_0}
$$

$$
[2] \space +(2(x + \Delta_3) - i - j - 1)P_{x + \Delta_3}
$$

$$
[3] \space -(2(x + \Delta_2) - i - j)P_{x + \Delta_2}
$$

$$
[4] \space -(2(x + \Delta_1) - i - j)P_{x + \Delta_1}
$$

接下来我们想将计算 $[1] + [3]$，$[2] + [4]$，我们先要对齐他们的系数，所以我们先改写 $[3],[4]$ 的系数：
$$
[1] \space +(2(x + \Delta_0) - i - j + 1)P_{x + \Delta_0}
$$

$$
[2] \space +(2(x + \Delta_3) - i - j - 1)P_{x + \Delta_3}
$$

$$
[3] \space -(2(x + \Delta_2) - i - j + 1)P_{x + \Delta_2} + P_{x + \Delta_2}
$$

$$
[4] \space -(2(x + \Delta_1) - i - j - 1)P_{x + \Delta_1} - P_{x + \Delta_1}
$$

我们考虑 $[1]+[3]$，我们从上面的 $①$ 知道：
$$
① (2(x + \Delta_0) - i - j + 1) P_{x + \Delta_0} \le (2(x + \Delta_i) - i - j + 1) P_{x + \Delta_i}
$$
所以 $[1] + [3]$：
$$
(2(x + \Delta_0) - i - j + 1)P_{x + \Delta_0} - (2(x + \Delta_2) - i - j + 1)P_{x + \Delta_2} + P_{x + \Delta_2} \le 0 + P_{x + \Delta_2} \le P_{x + \Delta_2}
$$
而对于 $[2] + [4]$，我们从上面的 $④$ 有：
$$
④(2(x + \Delta_3) - i - j - 1) P_{x + \Delta_3} \le (2(x + \Delta_i) - i - j - 1) P_{x + \Delta_i}
$$
所以 $[2] + [4]$：
$$
(2(x + \Delta_3) - i - j - 1)P_{x + \Delta_3} - (2(x + \Delta_1) - i - j - 1)P_{x + \Delta_1} - P_{x + \Delta_1} \le 0 - P_{x + \Delta_1} \le -P_{x + \Delta_1}
$$
所以 $[1] + [2] + [3] + [4]$ 有：
$$
[1] + [2] + [3] + [4] = ([1] + [3]) + ([2] + [4]) \le P_{x + \Delta_2} - P_{x + \Delta_1}
$$
接下来我们考察 $P_{x + \Delta_2} - P_{x + \Delta_1}$ 的正负性。

我们有两种情况：

第一，当我们的 $x + \Delta_2 \le x + \Delta_1$ 时，由于我们的村庄是一路向右的所以我们显然有 $P_{x + \Delta_2} \le P_{x + \Delta_1}$，那就有 $P_{x + \Delta_2} - P_{x + \Delta_1} \le 0$ 恒成立，那我们的原命题就为真。

第二，当我们的 $x + \Delta_2 > x + \Delta_1$ 时，这时我们就要改写 $[3],[4]$ 为：

$$
[1] \space +(2(x + \Delta_0) - i - j + 1)P_{x + \Delta_0}
$$

$$
[2] \space +(2(x + \Delta_3) - i - j - 1)P_{x + \Delta_3}
$$

$$
[3] \space -(2(x + \Delta_2) - i - j - 1)P_{x + \Delta_2} - P_{x + \Delta_2}
$$

$$
[4] \space -(2(x + \Delta_1) - i - j + 1)P_{x + \Delta_1} + P_{x + \Delta_1}
$$

然后我们改为计算 $[1]+[4]$ 和 $[2]+[3]$，同理最后会计算得到：
$$
[1] + [2] + [3] + [4] = ([1] + [4]) + ([2] + [3]) \le P_{x + \Delta_1} - P_{x + \Delta_2}
$$
所以我们最后变成要去看 $P_{x + \Delta_1} - P_{x + \Delta_2} \le 0$ 是否成立了，而 $x + \Delta_2 > x + \Delta_1$，所以一定有 $P_{x + \Delta_1} < P_{x + \Delta_2}$，故 $P_{x + \Delta_1} - P_{x + \Delta_2} \le 0$ 也是恒成立的，换言之在这种情况下，我们的原命题仍然为真。

第二步-证明f为凸

第一步证明 $f$ 为凸，即满足 $f[i][j] + f[i + 1][j + 1] \le f[i + 1][j] + f[i][j + 1]$。这要用到第一步的结论去证明。

我们的常规思路是去假设 $f[i][j+1]$ 取得最优解的转移点 $k$ 为 $x$，$f[i + 1][j]$ 取得最优解时转移点 $k$ 为 $y$。然后我们分 $x < y$ 和 $y < x$ 两种情况，将 $f[i][j]$ 和 $f[i+1][j+1]$ 各按 $k = x$ 或 $k = y$ 拆开之后，将拆出的 $w$ 应用上面证明得到的四边形不等式，再将各项合并成 $f[i][j+1] + f[i+1][j]$ 从而完成证明。下面我们进行具体的讲解。

我们知道 $f[i][j]$ 的转移为 $min(f[i - 1][k] + w[k + 1][j])$。

设 $f[i+1][j]$ 的最优转移点 $k = y$ ，则有：
$$
(1)f[i + 1][j] = f[i][y] + w[y + 1][j]
$$
设 $f[i][j + 1]$ 的最优转移点 $k = x$ ，则有：
$$
(2)f[i][j + 1] = f[i - 1][x] + w[x + 1][j + 1]
$$
我们计算 $(1) + (2)$ 就有：
$$
(3)f[i + 1][j] + f[i][j + 1] = f[i][y] + f[i - 1][x] + w[y + 1][j] + w[x + 1][j + 1]
$$

由于 $f[i][j]$ 的转移为 $min(f[i - 1][k] + w[k + 1][j])$，所以我们会有：
$$
(4)f[i][j] \le f[i - 1][x] + w[x + 1][j]
$$

$$
(5)f[i][j] \le f[i - 1][y] + w[y + 1][j]
$$

同理对于 $f[i + 1][j + 1]$ 我们也有：
$$
(6)f[i + 1][j + 1] \le f[i][x] + w[x + 1][j + 1]
$$

$$
(7)f[i + 1][j + 1] \le f[i][y] + w[y + 1][j + 1]
$$

接下来我们进行分类讨论。

1.当 $x \le y$ 时

我们计算 $(4)+(7)$ 得：
$$
f[i][j] + f[i + 1][j + 1] \le f[i - 1][x] + f[i][y] + w[x + 1][j] + w[y + 1][j + 1]
$$
而对于 $w[x + 1][j] + w[y + 1][j + 1]$，$x + 1 \le y + 1$，$j < j + 1$，由我们上面证明的 $w$ 的凸性就有：
$$
w[x + 1][j] + w[y + 1][j + 1] \le w[y + 1][j] + w[x + 1][j + 1]
$$
我们带回 $(4)+(7)$ 得到的不等式就有：
$$
f[i][j] + f[i + 1][j + 1] \le f[i - 1][x] + f[i][y] + w[y + 1][j] + w[x + 1][j + 1]
$$
我们调换一下顺序就有：
$$
f[i][j] + f[i + 1][j + 1] \le (f[i - 1][x] + w[x + 1][j + 1]) + (f[i][y] + w[y + 1][j])
$$
代入 $(1)$ 和 $(2)$ 就有：
$$
f[i][j] + f[i + 1][j + 1] \le f[i][j + 1] + f[i + 1][j]
$$

2.当 $x>y$ 时

我们计算 $(5)+(6)$ 得：
$$
f[i][j] + f[i + 1][j + 1] \le f[i][x] + f[i - 1][y] + w[x + 1][j + 1] + w[y + 1][j]
$$
我们不等式左右两边分别减去 $(3)$ 的对应边，就有：
$$
f[i][j] + f[i + 1][j + 1] - (f[i + 1][j] + f[i][j + 1]) \le f[i][x] + f[i - 1][y] + w[x + 1][j + 1] + w[y + 1][j] - (f[i][y] + f[i - 1][x] + w[y + 1][j] + w[x + 1][j + 1])
$$
我们发现不等式右边 $w$ 相关项就约掉了，所以有：
$$
(8)f[i][j] + f[i + 1][j + 1] - (f[i + 1][j] + f[i][j + 1]) \le f[i][x] + f[i - 1][y] - f[i][y] - f[i - 1][x]
$$
我们观察 $(8)$ 的左右两边发现时形式相似的类似的东西。因为我们有 $i > i - 1$ 和 $x > y$，所以其实也是凸性的那个式子形式。

所以我们假设四边形不等式不成立，即假设：
$$
f[i][j] + f[i + 1][j + 1] - (f[i + 1][j] + f[i][j + 1]) > 0
$$
所以由 $(8)$ 不等式右边根据关系也要大于 $0$：
$$
(9)f[i][x] + f[i - 1][y] - f[i][y] - f[i - 1][x] > 0
$$

也就是说，我们只要证明出 $(9) \le 0$，就能证明出“四边形不等式不成立”这一命题不成立，也就是说四边形不等式成立。那我们如何证明呢？

我们可以用类似与递归的思想去思考这个问题，我们现在将 $f[i][j] + f[i + 1][j + 1] - (f[i + 1][j] + f[i][j + 1])$ 的正负性通过设出转移点 $x$ 和 $y$ 归约到一个规模更小的问题 $f[i][x] + f[i - 1][y] - f[i][y] - f[i - 1][x]$ 的正负性上。

那我们同样可以设出 $f[i][y]$ 的最优转移点是 $x'$，$f[i - 1][x]$ 的最优转移点是 $y'$ 将 $f[i][x] + f[i - 1][y] - f[i][y] - f[i - 1][x]$ 的正负性又归约到一个更小的问题上。那在这个更小的问题上，我们同样考虑，如果 $x' \le y'$ 那我们就用上面的结论就得证了；但如果 $x' > y'$，那我们就继续规约到一个更更小的问题……

我们发现，随着我们不断规约，我们每一轮设的最优转移点一定是单调下降的，那到了最后一定有 $x = y = 0$，那就满足了 $x \le y$ 就得证了。所以其实是下面大概这样一个二叉树结构，但是保证最下层由于 $x = y = 0$ 也就是一定从 $0$ 转移来，所以只有一个叶子。

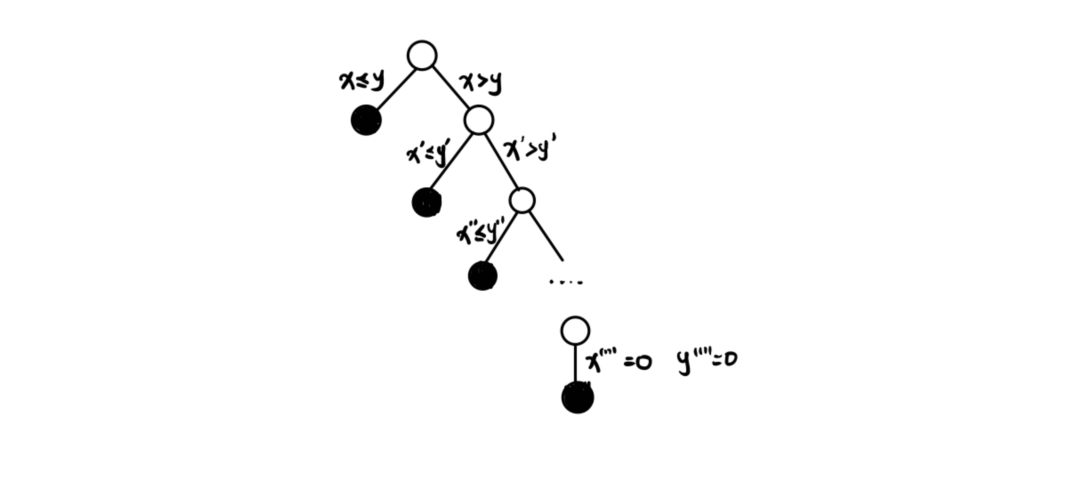
所以不论如何，从根出发的任意到叶子路径最后一定规约到 $x \le y$ 也就是上面已经证明了的情况。

第三步-证明转移点k的性质

我们设 $K[i][j]$ 为 $f[i][j]$ 的决策点，下面我们证明 $K[i][j - 1] \le K[i][j] \le K[i + 1][j]$。即我们决策点的单调性。

证明 $K[i][j - 1] \le K[i][j]$ 时，设 $f[i][j - 1]$ 取最优解时转移点 $k=y$，对所有的 $x \neq y$ 令 $x \le y$，我们就有 $x + 1 \le y + 1\le j - 1 < j$。

我们的目标是要证明：
$$
f[i][j - 1](k = x) + f[i][j](k = y) \le f[i][j - 1](k = y) + f[i][j](k = x)
$$
然后我们把他们一项一项拆开：
$$
f[i][j - 1](k = x) = f[i - 1][x] + w[x + 1][j - 1]
$$

$$
f[i][j](k = y) = f[i - 1][y] + w[y + 1][j]
$$

$$
f[i][j - 1](k = y) = f[i - 1][y] + w[y + 1][j - 1]
$$

$$
f[i][j](k = x) = f[i - 1][x] + w[x + 1][j]
$$

我们如果只看 $w$ 项，那自然满足一个四边形不等式：
$$
(1)w[x + 1][j - 1] + w[y + 1][j] \le w[y + 1][j - 1] + w[x + 1][j]
$$
而左右两边的 $f$ 项是一样的：
$$
(2)f[i - 1][x] + f[i - 1][y] = f[i - 1][y] + f[i - 1][x]
$$
所以我们 $(1) + (2)$ 就得到了我们要证明的原命题为真，即得到了：
$$
f[i][j - 1](k = x) + f[i][j](k = y) \le f[i][j - 1](k = y) + f[i][j](k = x)
$$
也就是：
$$
f[i][j - 1](k = x) - f[i][j - 1](k = y) \le f[i][j](k = x) - f[i][j](k = y)
$$
这时我们就会发现因为我们的最优转移点是 $y$ 所以一定有 $f[i][j - 1](k = y) \le f[i][j - 1](k = x)$，也就是上述不等式左边会小于等于 $0$。那么对于右边移向后就一定会有 $f[i][j](k = y) \le f[i][j](k = x)$。

也就是说对于所有小于 $y$ 的 $x$，都会有 $f[i][j - 1](k = y) \le f[i][j - 1](k = x)$，那么也都会有 $f[i][j](k = y) \le f[i][j](k = x)$。

因此我们令 $f[i][j]$ 取得最优解的 $k$ 一定不小于 $y$，这就完成了对 $K[i][j - 1] \le K[i][j]$ 的证明。对于 $K[i][j] \le K[i + 1][j]$ 的证明是类似的。

而对于 $K[i][j] \le K[i + 1][j]$ 也是类似的只不过用到的是 $f$ 的四边形不等式，在这里就不赘述了。

代码实现

那到现在，我们已经证明得到了不论是增加一个邮局还是增加一个村庄，我们的决策点都是向右移动的，那我们接下来要怎么样快速转移呢？

这很简单，既然我们已经知道了 $K[i][j - 1] \le K[i][j] \le K[i + 1][j]$，那我们就按照第一层 $j$ 从小到大，第二层 $i$ 从大到小，第三层枚举转移点从 $K[i][j - 1]$ 到 $K[i + 1][j]$ 就可以了，枚举完找到最优转移点后又用来更新 $K[i][j]$，这样的话转移的复杂度就压下来了。

接下来是预处理 $w[i][j]$ 的复杂度也要压下来，否则时间复杂度还是 $O(n^3)$。我们知道 $w[i][j]$ 是在第 $i$ 到第 $j$ 个村庄建一个邮局的最小距离和，前面提到在中点村庄上建，可以推出如下式子 $w[i][j]=w[i][j-1]+abs(x[j]-x[(i+j)/2])$。

考虑两种情况，一种是 $(i+j-1) \% 2=0$，这时 $(i+j)/2=(i+j-1)/2$，故建邮局的村庄不变，只要把新村庄到原邮局的距离加进 $w[i][j]$ 即可；

对于 $(i+j-1) \% 2=1$ 时，新邮局要在原邮局位置往右挪一位，举个例子：

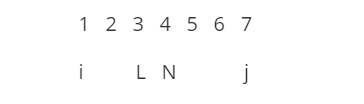
（其中L表示原邮局，N表示新邮局）

我们发现移动邮局后，对于村庄 $1$、$2$、$3$，距离都增加了 $x[4]-x[3]$，而对于区间 $4$、$5$、$6$，距离都减少了$x[4]-x[3]$，所以对于前 $i$ 到 $j-1$ 个邮局，距离和是不变的，只要把新村庄到新邮局的距离加进 $w[i][j]$ 即可。这样的话就可以在 $O(n^2)$ 完成预处理了。

所以我们总的代码实现如下：

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
int n, m;
long long x[1100];
long long w[1100][1100], f[1100][1100], K[1100][1100];
int main() {
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++) scanf("%lld", &x[i]);

    //预处理w数组
    for(int i = 1; i <= n; i++) {
        for(int j = i; j <= n; j++) {
            if(i == j) w[i][j] = 0;
            else {
                int mid = (i + j) / 2;
                w[i][j] = w[i][j - 1] + x[j] - x[mid];
            }
        } 
    } 

    memset(f, 63, sizeof(f));
    for(int i = 0; i <= m; i++) f[i][0] = 0;

    for(int j = 1; j <= n; j++) {
        K[m + 1][j] = n;
        for(int i = m; i >= 1; i--) {
            for(int k = K[i][j - 1]; k <= K[i + 1][j]; k++) {
                long long val = f[i - 1][k] + w[k + 1][j];
                if(val < f[i][j]) {
                    f[i][j] = val;
                    K[i][j] = k;
                }
            }
        }
    }

    printf("%lld", f[m][n]);
    return 0;
} 

[HNOI2008]玩具装箱

题目描述

教授要去看奥运，但是他舍不下他的玩具，于是他决定把所有的玩具运到北京。他使用自己的压缩器进行压缩，其可以将任意物品变成一堆，再放到一种特殊的一维容器中。

$P$ 教授有编号为 $1...N$ 的 $N(1 \le N \le 5 * 10^4)$ 件玩具，第 $i$ 件玩具经过压缩后变成一维长度为 $C_i(1 \le C_i \le 10^7)$.为了方便整理， $P$ 教授要求在一个一维容器中的玩具编号是连续的。同时如果一个一维容器中有多个玩具，那么两件玩具之间要加入一个单位长度的填充物，形式地说如果将第i件玩具到第j个玩具放到一个容器中，那么容器的长度将为 $x=j-i+\sum(C_k)$，其中 $i ≤ k ≤ j$。

制作容器的费用与容器的长度有关，根据教授研究， 如果容器长度为 $x$, 其制作费用为 $(X-L)^2$。其中 $L(1 \le L \le 10^7)$ 是一个常量。$P$ 教授不关心容器的数目，他可以制作出任意长度的容器，甚至超过 $L$。但他希望费用最小。

解题思路

这道题的具体解法我们在斜率优化当中已经讲过了，感兴趣的同学可以传送过去复习一下。

我们考虑用四边形不等式证明一下单调性，一般只证明 $w[i][j]$ 的单调性后面都可以省略都是对的，但不排除有时是有特殊情况的，但这种情况就放弃吧。所以在这里我们就要证明 $f[i] = min(f[j] + (s[i] - s[j] - 1 - L)^2)$ 的单调性。

我们改写 $f[i] = min(f[j] + w[i][j])$，那么就有 $w[i][j] = (s[i] - s[j] - 1 - L)^2$。

我们设 $Q = s[i] - s[j] - 1 - L$，则有：
$$
(1)w[i][j] = Q^2
$$

我们写出 $w[i + 1][j + 1]$：
$$
w[i + 1][j + 1] = (s[i + 1] - s[j + 1] - 1 - L)^2
$$
我们还有 $s[i + 1] = s[i] + c[i + 1] + 1$ 和 $s[j + 1] = s[j] + c[j + 1] + 1$，我们展开：
$$
w[i + 1][j + 1] = ((s[i] + c[i + 1] + 1) - (s[j] + c[j + 1] + 1) - 1 - L)^2
$$
化简得到：
$$
(2)w[i + 1][j + 1] = (Q + c[i + 1] - c[j + 1])^2
$$
同理我们写出 $w[i][j + 1]$：
$$
w[i][j + 1] = (s[i] - s[j + 1] - 1 - L)^2 = (s[i] - (s[j] + c[j + 1] + 1) - 1 - L)^2
$$
化简就得到：
$$
(3)w[i][j + 1] = (Q - c[j + 1] - 1)^2
$$
最后我们写出 $w[i + 1][j]$：
$$
w[i + 1][j] = (s[i + 1] - s[j] - 1 - L)^2 = ((s[i] + c[i + 1] + 1) - s[j] - 1 - L)^2
$$
化简就得到：
$$
(4)w[i + 1][j] = (Q + c[i + 1] + 1)^2
$$
我们计算 $(1) + (2) - (3) - (4)$，化简就有：
$$
w[i][j] + w[i + 1][j + 1] - w[i + 1][j] - w[i][j + 1] = -2(c[i + 1] + 1)(c[j + 1] + 1)
$$
有 $c[i],c[j] \ge 1$，所以我们有：
$$
-2(c[i + 1] + 1)(c[j + 1] + 1) \le -8
$$
所以就会有：
$$
w[i][j] + w[i + 1][j + 1] \le w[i + 1][j] + w[i][j + 1]
$$
所以四边形不等式成立，此方程具有决策单调性。

结语

通过这篇 $BLOG$，相信你已经对四边形不等式有了一定的理解。到这为止，我们的动态规划系列就要接近尾声了。后面可能会更新一些计数类动态规划或者插头动态规划之类的。最后希望你喜欢这篇BLOG！