在接下来的两篇BLOG里,我们会一起探讨大规模的机器学习的相关问题。所谓大规模机器学习就是用来处理大数据的算法,如果我们看近5到10年的机器学习的历史,你会发现现在的学习算法比5年前的好很多其中的重要原因之一就是我们现在拥有很多可以训练算法的数据。所以巧妙地运用大量数据可以让我们的算法事半功倍。
大规模机器学习
为什么我们喜欢用大的数据集呢? 我们已经知道得到一个高效的机器学习系统的最好的方式之一就是用一个低偏差的学习算法并且用大量的数据来训练它。比如我们在很早之前提到过的一个区分易混淆词组的例子。通过增加训练集大小我们对各种算法进行比较:
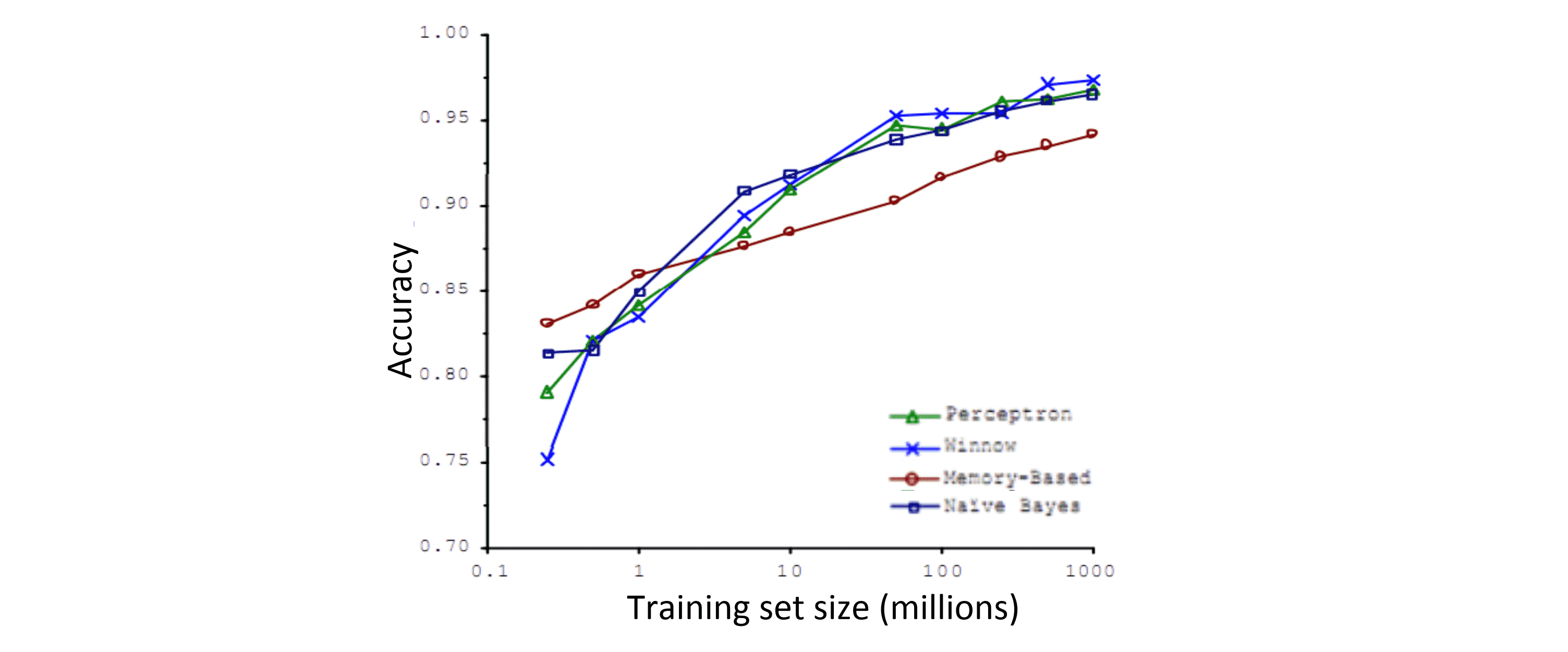
我们发现当数据集不断增大时,开始最劣的算法可能会变成最优的算法。换句话说通常不是最好的算法胜出,而是最多的数据胜出。因此在可能的条件下,我们会想得到尽可能大的数据集。
但训练大的数据集也有它自己的问题,特别是计算量的问题。假设我们的训练集的大小 m 是 100,000,000 ,这对于现代的数据集其实是很现实的,如果我们看中国的人口普查数据集,中国就有13亿人,在当今社会我们经常能遇到动辄上亿的记录,比如我们看一下很受欢迎的网站的浏览量,我们很容易得到至少上亿条的记录。那么此时假设我们要训练一个线性回归模型或者是逻辑回归模型,我们就要使用如下的梯度下降规则:
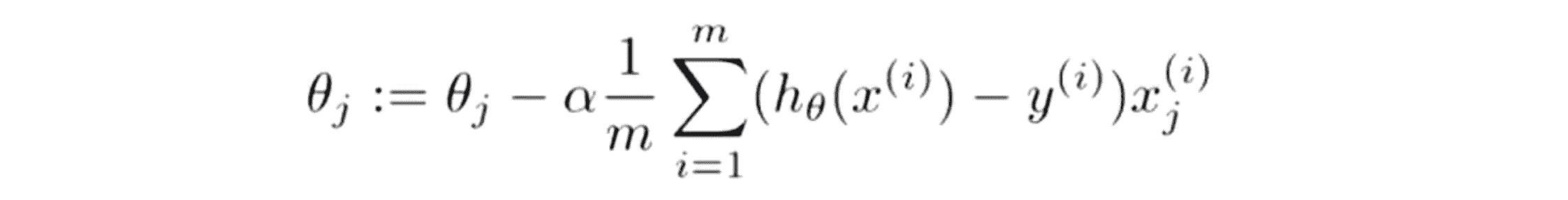
当我们在看需要些什么来算梯度的时候,也就是右边的这个项,当 m 是一个亿的时候,我们每次下降都需要加一亿个项来计算这些导数项,这个时间我们显然是不能接受的。那我们有什么优化的方法吗?这时首先我们应该问自己,为什么要用这么大的数据呢?能不能缩小数据集只用其中的几千条数据呢?也许我们可以随机从上亿条的数据集里选个一千条的子集然后用我们的算法计算。所以在我们投资精力和开发软件来训练大数据的模型之前,往往作为一个很好的检查是去检查小一些的数据集是不是好用,我们通常的方法是画学习曲线。如果你画了学习曲线而且你的训练目标看上去像下面这样:
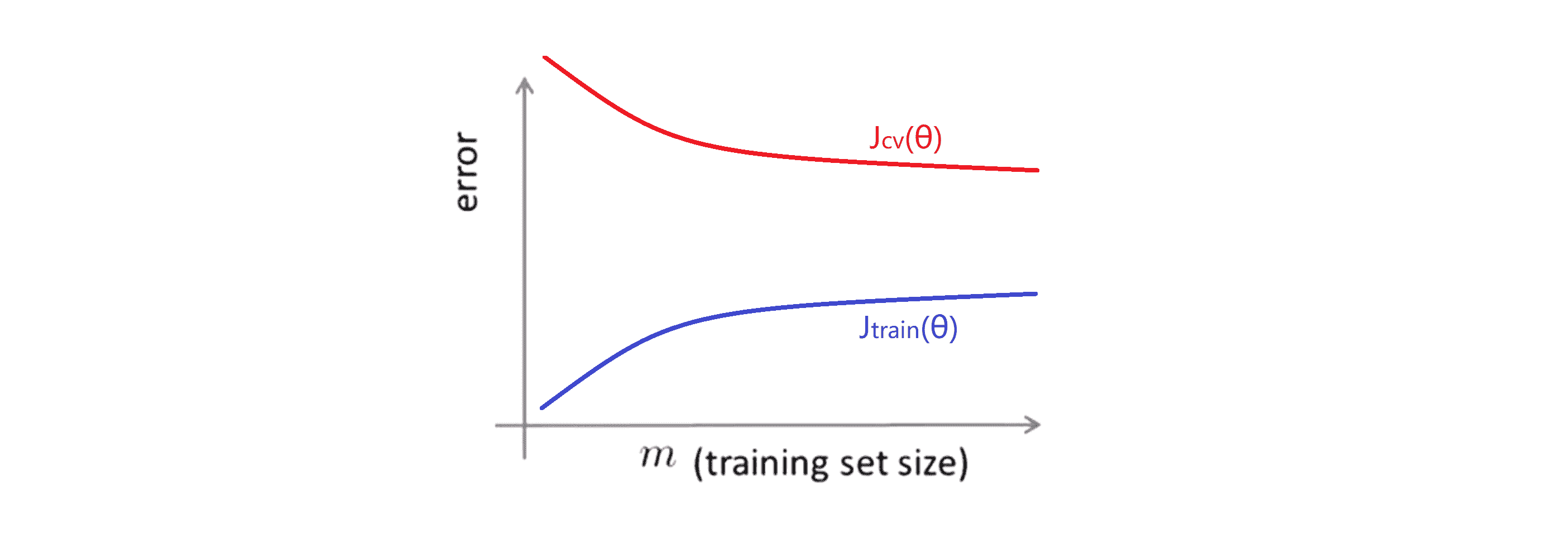
这看起来像高方差的学习算法,我们就会对增加训练集的大小来提高性能更有信心。
而相比之下如果我们画的学习曲线是下面这样的:
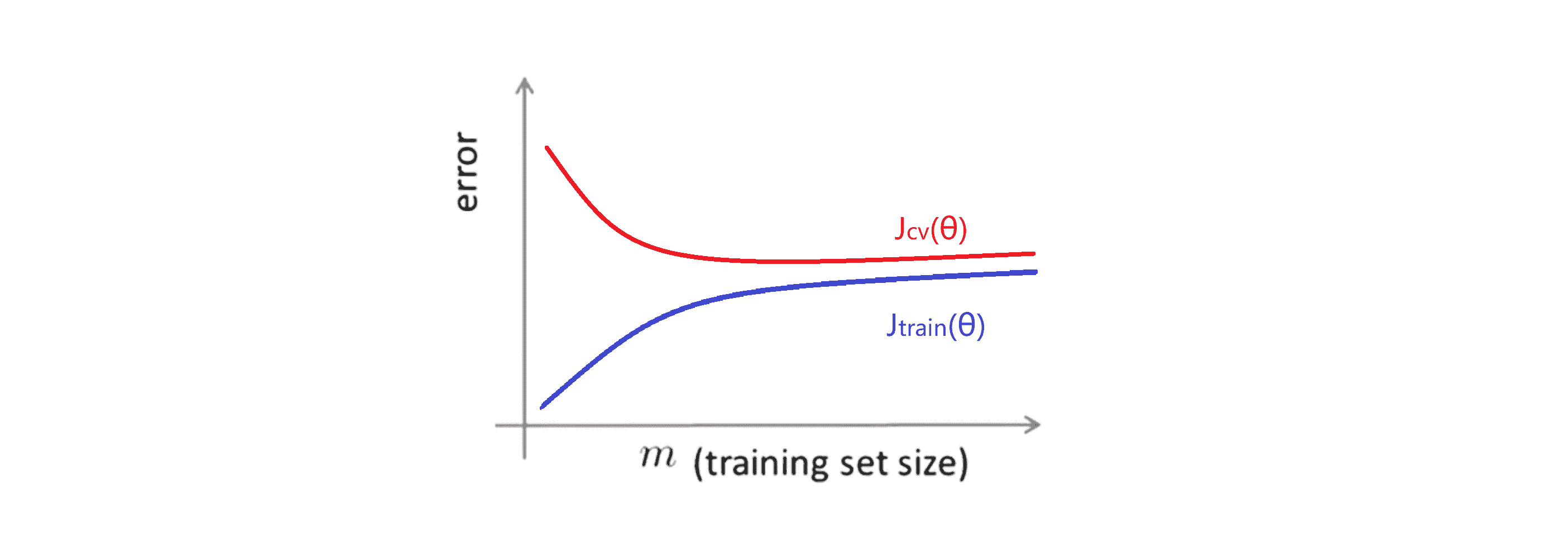
这看起来像经典的高偏差学习算法,这时看上去把数据集大小 m 增加到上亿会不一定会好很多,所以我们继续用 m 等于1000就很好了,而不是花很多精力去找出这个算法的规模。
当然,如果我们的情况是上图所示,一个很自然的方法是多加一些特征或者在你的神经网络里加一些隐藏的单元等等。最后我们又会变成一个像下边的高方差的图:

也许这相当于m等于1000的状况,这给我们更多的信心去花时间去改进算法来适应更大的数据点。在接下来的部分中,我们会看到几个主要的想法来改造我们的算法来处理大数据集。
随机梯度下降
对于很多机器学习算法,包括线性回归、逻辑回归、神经网络等等,算法的实现都是通过得出某个代价函数或者某个最优化的目标来确定算法目的,然后使用梯度下降这样的方法来求得代价函数的最小值来得到答案的。
假如我们要使用梯度下降法来训练某个线性回归模型,那我们的假设函数和代价函数会是下面这样的:
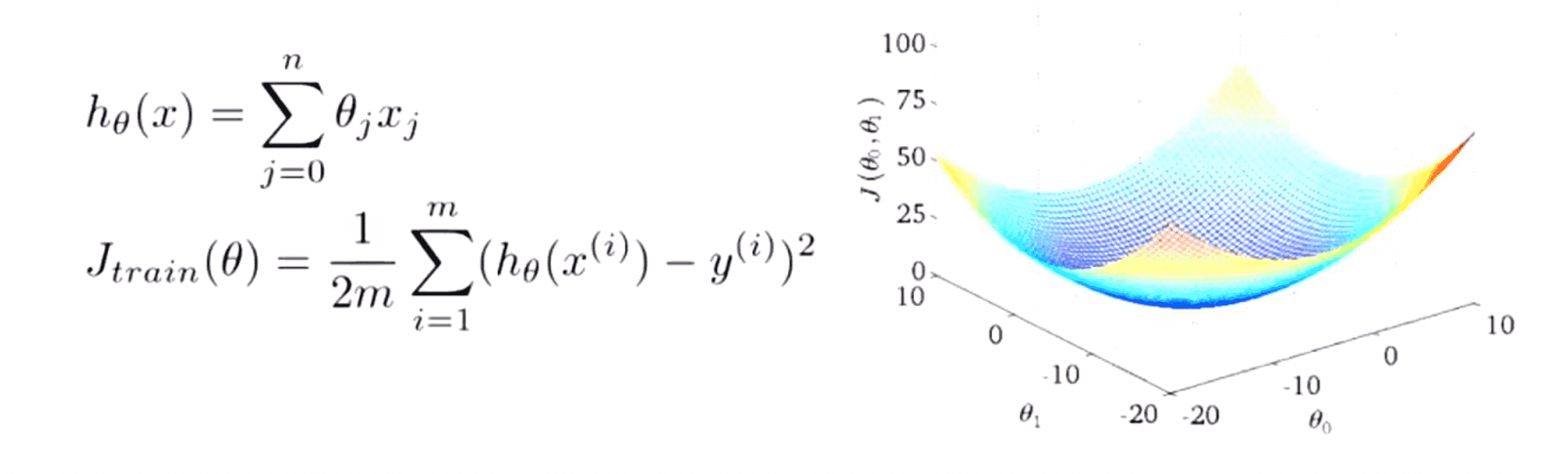
如果我们画出以 θ0 和 θ1 为参数的代价函数 J,就会是上图的右边这样的弓形函数。下面就是梯度下降算法的详细过程,在内层循环中,我们需要用下面这个式子反复更新参数 θ 的值:
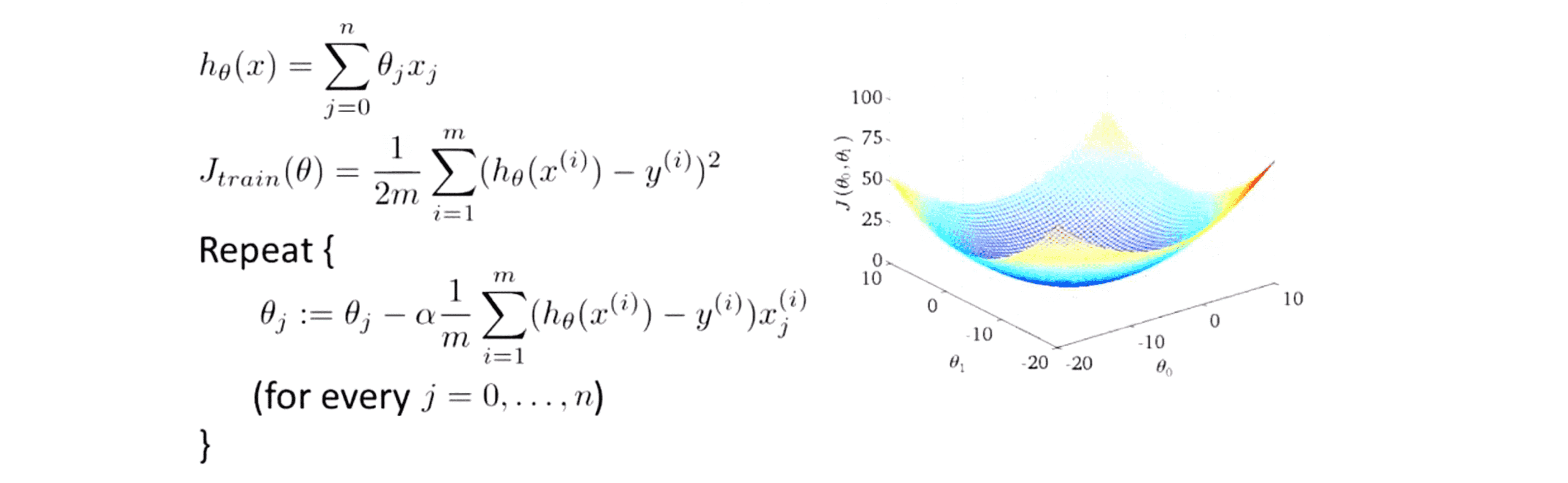
下图表示的是梯度下降迭代的具体做法,假设这个叉表示了参数的初始位置:
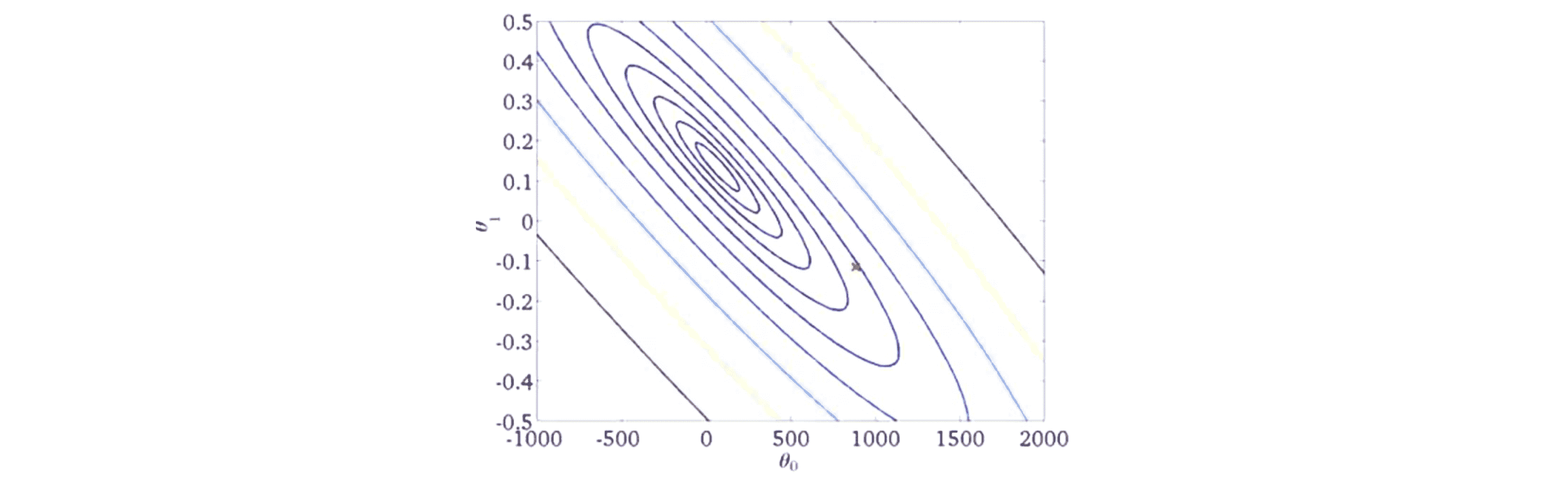
那么在你运行梯度下降的过程中,多步迭代最终会将参数锁定到全局最小值,迭代的轨迹看起来非常快地收敛到全局最小:
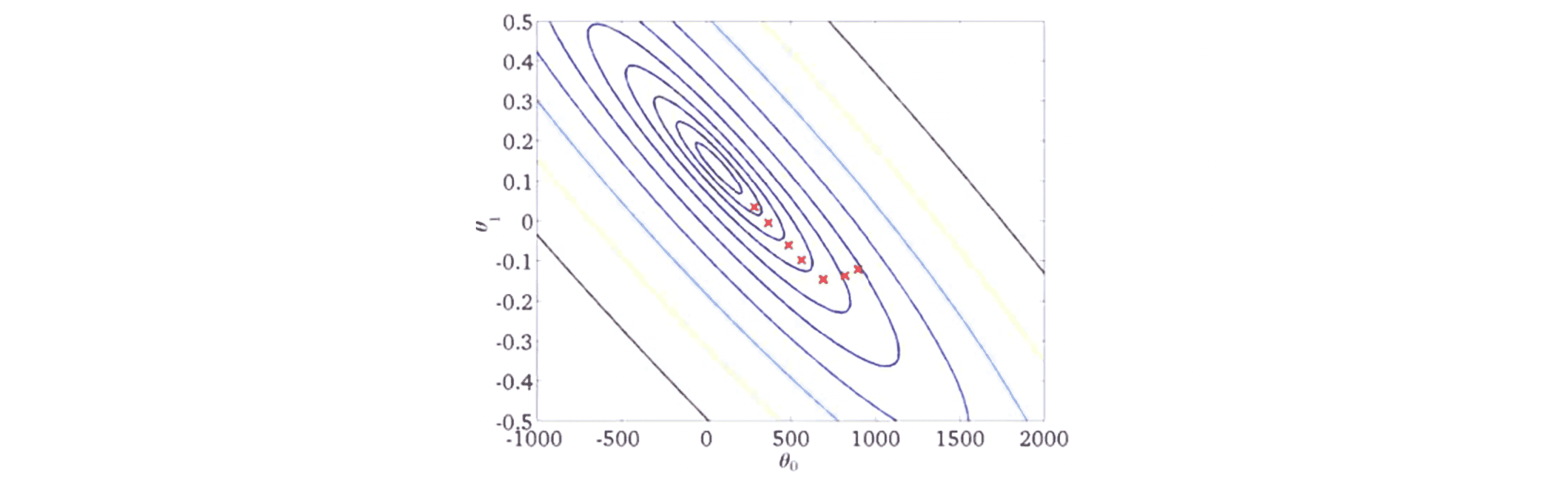
这看起来很美好但梯度下降法的问题是当数据集大小 m 值很大时,我们计算这个微分项的计算量就变得很大,因为每次迭代都需要对所有 m 个训练样本求和,所以假如是中国人口普查数据就有十亿量级的数据记录,这样的时间复杂度是我们不太能接受的。而这种普通的梯度下降算法也被称为批量梯度下降(batch gradient descent), “批量”就表示我们需要每次都考虑所有的训练样本,其在大数据下的表现确实比进入人意。
相比于批量梯度下降,当我们的训练集较大时,一种叫做随机梯度下降(stochastic gradient descent)的算法表现得可能更加出色,那么它具体是1怎么工作的呢。
相比较于批量梯度下降算法的迭代过程:

随机梯度下降在每一步迭代中不去考虑全部的训练样本,而是只需要考虑一个训练样本。在开始介绍新的算法之前,我们把批量梯度下降算法的代价函数写在下图这里,我们发现其代价函数和批量梯度下降算法的定义有一点区别,我们定义参数 θ 关于训练样本(x(i),y(i))的代价等于二分之一倍的我们的假设h(x(i))跟实际输出y(i)的误差的平方,因此这个代价函数值实际上测量的是我的假设在某个样本(x(i),y(i))上的表现。你可能已经发现总体的代价函数Jtrain可以被写成在所有m个训练样本中我们下面这种的每一个样本(x(i),y(i))上的代价函数的平均值:

将上面的代价函数应用到线性回归中让我们来得出随机梯度下降的算法:
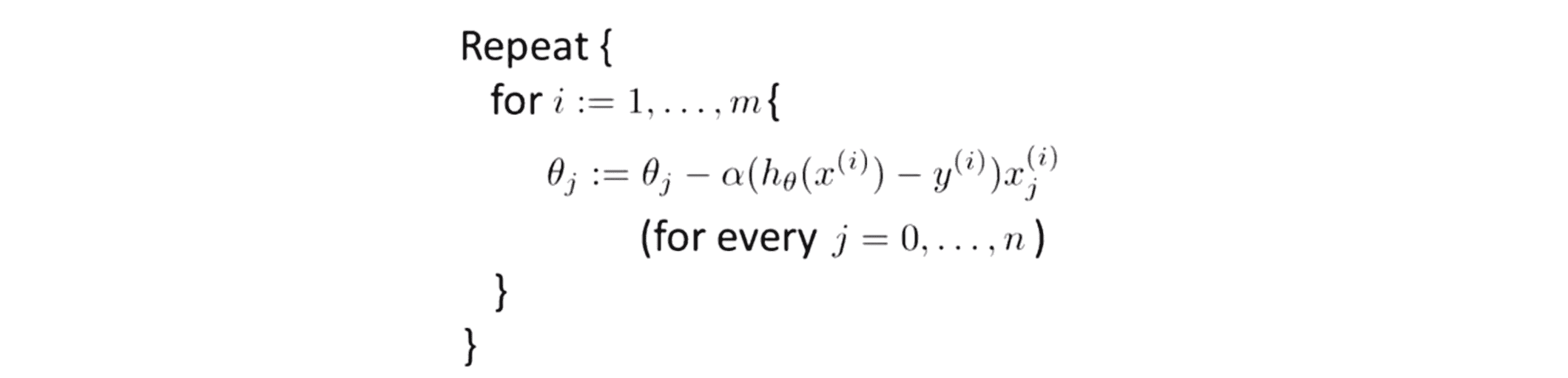
随机梯度下降法的第一步是将所有数据打乱,我说的随机打乱的意思是将所有m个训练样本重新排列,这就是标准的数据预处理过程;然后随机梯度下降的主要算法如上,在i等于1到m中进行循环,也就是对所有m个训练样本进行遍历,然后进行如下更新:我们按照这样的公式进行更新θj=θj-α(h(x(i))-y(i)x(i)j),同样还是对所有j的值进行更新。不难发现这一项实际上就是我们批量梯度下降算法中求和式里面的那一部分,事实上如果你数学比较好的话你可以证明这一项是等于之前那个代价函数关于参数θj的偏微分。
所以简单来说随机梯度下降的做法实际上就是扫描所有的训练样本,首先是我的第一组训练样本(x(1),y(1)) 然后只对这第一个训练样本对它的代价函数计算一小步的梯度下降。换句话说我们要关注第一个样本,然后把参数θ稍微修改一点使其对第一个训练样本的拟合变得好一点。完成这个内层循环以后再转向第二个训练样本,然后还是一样在参数空间中进步一小步,也就是稍微把参数修改一点,让它对第二个样本的拟合更好一点;做完第二个再转向第三个训练样本,同样还是修改参数让它更好的拟合第三个训练样本……以此类推直到完成所有的训练集。然后外部这个repeat重复循环会多次遍历整个训练集,从这个角度分析随机梯度下降算法我们就能更好地理解为什么一开始要随机打乱数据,这这保证了我们在扫描训练集时对训练集样本的访问是随机的顺序,不管你的数据是否已经随机排列过或者一开始就是某个奇怪的顺序都可以得到几乎一样的结果。
随机梯度下降跟批量梯度下降不同之处就在于随机梯度下降不需要等到对所有m个训练样本求和来得到梯度项,而是只需要对单个训练样本求出这个梯度项。换句话说我们可以在读入的过程中就开始优化参数了,不用等到把所有那13亿的中国人口普查的数据拿来遍历一遍扫描一遍,然后才一点点地修改参数直到达到全局最小值。对随机梯度下降来说我们只需要一次关注一个训练样本,而我们已经开始一点点把参数朝着全局最小值的方向进行修改了。
让我们通过图片来看看这个算法是如何更新参数θ的:
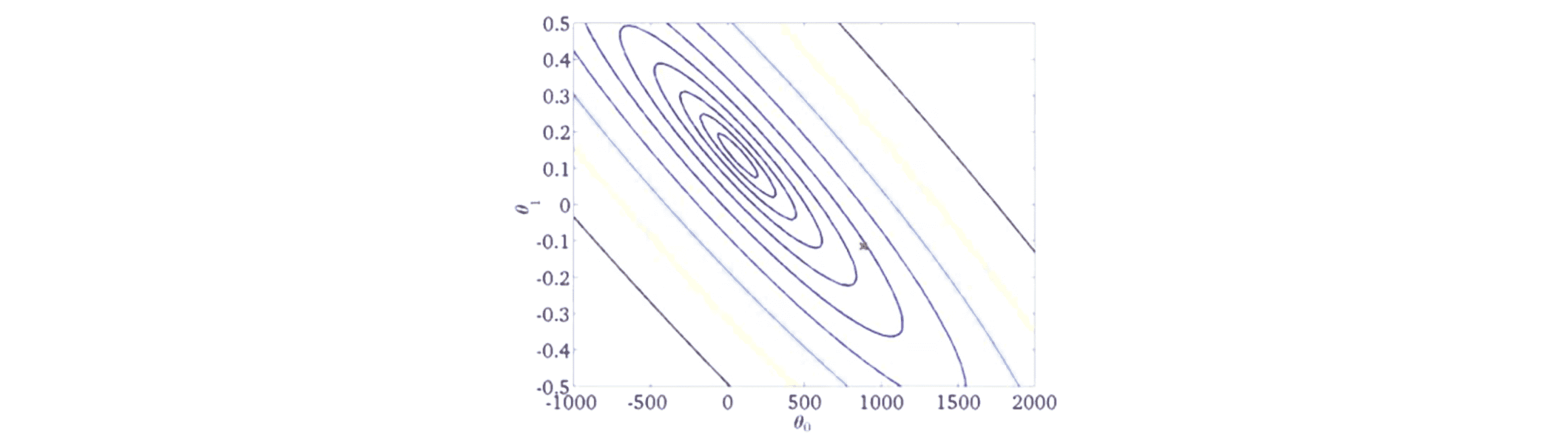
之前我们已经看到当使用批量梯度下降的时候需要同时考虑所有的训练样本数据,所以批量梯度下降的收敛过程会倾向于下图中上面这条一条近似的直线,其一直找到全局最小值;与此不同的是在随机梯度下降中每一次迭代都会更快,因为我们不需要对所有训练样本进行求和,所以在我们运行随机梯度下降的过程中会发现一般来讲其参数是朝着全局最小值的方向被更新的但也不一定,其看起来它是以某个比较随机、迂回的路径在朝全局最小值逼近,就如下图中下面那条蜿蜒的路径一样:
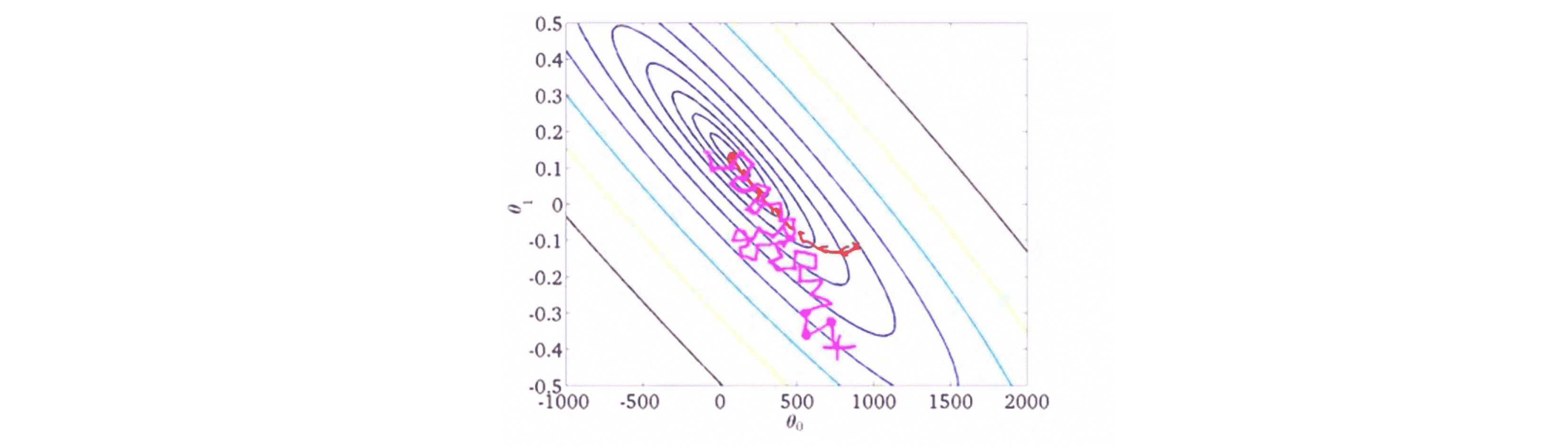
实际上就如上图一样,我们运行随机梯度下降和批量梯度下降两种方法的收敛形式是不同的,随机梯度下降是在某个靠近全局最小值的区域内徘徊而不是直接逼近全局最小值并停留在那点。但实际上这并没有多大问题,只要参数最终移动到某个非常靠近全局最小值的区域内,就会得出一个较为不错的假设。所以通常我们用随机梯度下降法也能得到一个很接近全局最小值的参数,这对于绝大部分实际应用的目的来说已经足够了。
最后一点细节 在随机梯度下降中,我们有一个外层的repeat循环,它决定了内层循环的执行次数,所以外层循环应该执行多少次呢?这其实取决于训练样本的大小。通常1次就够了,最多到10次是比较典型的,所以我们可以循环执行内层1到10次。因此如果我们有非常大量的数据比如中国普查的人口数据比如说的13亿人口数据的例子,每次我们只需要考虑一个训练样本,这里的i就是从1到13亿了,所以可能你每次只需要考虑一个训练样本,就能训练出非常好的假设。这时由于m非常大,那么外层循环只用做一次就够了。但通常来说循环1到10次都是非常合理的,这还是取决于你训练样本的大小。
如果你跟批量梯度下降比较一下的话,批量梯度下降在一步梯度下降的过程中就需要考虑全部的训练样本,所以批量梯度下降就是这样微小而精准的一次次移动,这也是为什么随机梯度下降法要快得多。
Mini-Batch 梯度下降
在上一部分,我们初步学习了随机梯度下降算法的算法实现原理,这一部分就让我们讨论基于这些方法的另一种变形叫做Mini-Batch梯度下降法,这种算法有时候甚至比随机梯度下降还要快一点。
在批量梯度下降中,我们每次迭代我们都要用所有的 m 个样本,在随机梯度下降中每次迭代我们只用 1 个样本,而Mini-Batch 梯度下降做的介于它们之间。准确地说在这种方法中我们每次迭代使用 b 个样本,b 是一个叫做"Mini-Batch"的参数,所以这种算法介于随机梯度下降和批量梯度下降之间:
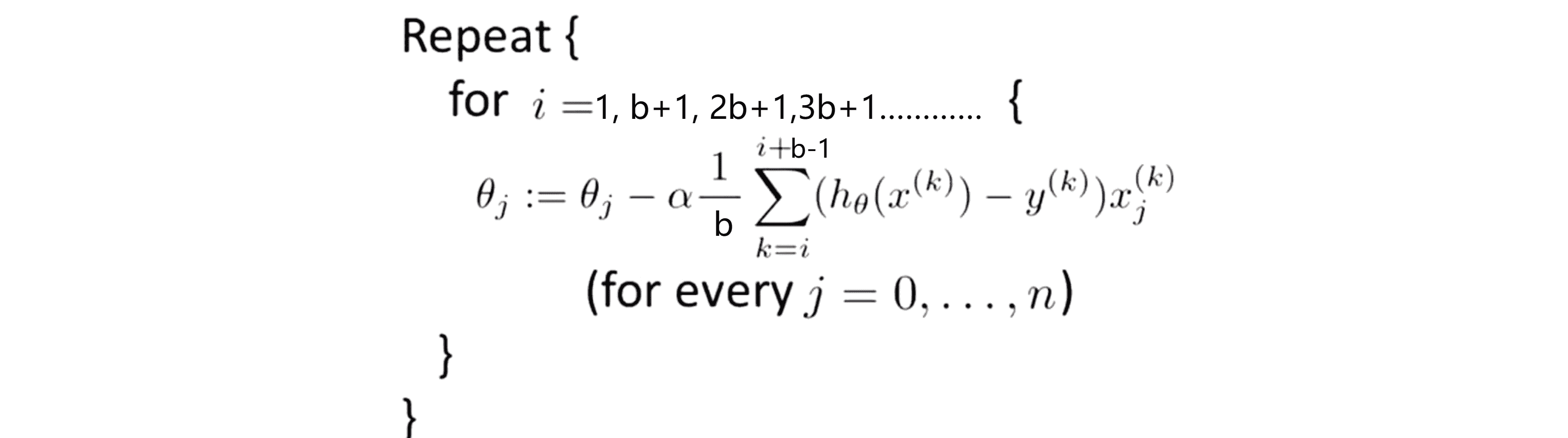
这就像批量梯度下降只不过我们会用小很多的批量规模,其中b的一个标准取值可能是2到100之间的任何一个数比如说 10,我们算法思想是我们每次用 b 个样本而不是每次用 1 个或者 m 个,所以让我正式地把这种情况下的梯度下降写出来

我们将要确定 b 例如我们假设 b 是10,所以我们将要从训练集中取出接下来的 10 个样本,则对于每一次迭代,训练集是样本 (x(i).y(i)) 到(x(i+9),y(i+9)) 的集合,然后我们将要用这10个样本做一个实际上是梯度下降的更新,因此我们每次迭代更新就是学习速率α乘以1/10乘以 k 对 h (x(k)-y(k))×x(k)j 从 i 到 i+9 求和。因此完整地讲完整个算法,为了简化刚才的这个索引,我将假设我有小批量规模为10和一个大小为1000的训练集,我们接下来要做的就是计算这个形式的和,从i等于1、11、21等等开始步长是10因为我们每次处理10个样本,然后我们每次对10个样本使用这种梯度下降来更新一直到991结束。
这就是Mini-Batch 梯度下降的完整过程,其实就是随机梯度下降算法的一种普遍形式。相比批量梯度下降这种算法也让我们进展快很多,比如让我们再次处理中国13亿人的人口普查数据训练集,我们要做的是在处理了前10个样本之后,我们可以开始优化参数 θ ,因此我们不需要扫描整个训练集我们只要处理前10个样本然后这可以让我们有所改进,接着我们可以处理第二组10个样本再次对参数做一点改, 然后接着这样做……因此这就是Mini-Batch 梯度下降比批量梯度下降快的原因,我们可以在只处理了10个样本之后就改进参数而不是需要等到我们完整扫描完13亿个样本中的每一个再进行优化。那么Mini-Batch 梯度下降和随机梯度下降比较又怎么样呢?也就是说为什么我们想要每次处理b个样本而不是像随机梯度下降一样每次处理一个样本?答案是——向量化!具体来说Mini-Batch 梯度下降可能比随机梯度下降好仅当我们有好的向量化实现时,在那种情况下 10 个样本求和可以用一种更向量化的方法实现,允许你部分并行计算10个样本的和。换句话说 使用正确的向量化方法计算剩下的项我们有时可以使用好的数值代数库来部分地并行计算b个样本让我们的算法跑得更加快。且每次处理b个而不是一个也让算法的下降更加稳健。
但Mini-Batch 梯度下降的一个缺点是有一个额外的参数 b,我们需要单独花时间调试小批量大小,但是如果我们有一个好的向量化实现这种方法有时甚至比随机梯度下降更快这就很值得了。
好了这就是小批量梯度下降算法,在某种意义上其做的事情介于随机梯度下降和批量梯度下降之间,如果我们选择合理的b的值比如我经常选择b等于10再加上一个好的向量化实现有时它可以比随机梯度下降和批量梯度下降更快。
随机梯度下降收敛
现在我们已经知道了随机梯度下降算法和Mini-Batch 梯度下降,但是当我们运行这个算法时,该如何确保调试过程已经完成并且能正常收敛呢?还有同样重要的是我们应该怎样调整随机梯度下降中学习速率α的值呢?在这一部分,我们会谈到一些方法来处理这些问题确保它能收敛以及选择合适的学习速率α。
回到我们之前批量梯度下降的算法,我们确定梯度下降已经收敛的一个标准方法是画出最优化的代价函数关于迭代次数的变化。下图就是代价函数:
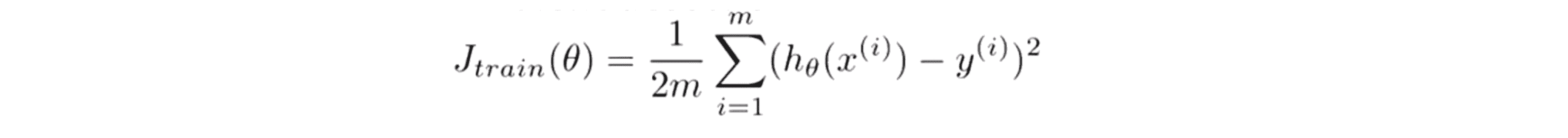
我们要保证这个代价函数在每一次迭代中都是下降的,当训练集比较小的时候我们不难完成,因为要计算这个求和是比较方便的;但当我们的训练集非常大的时候我们不希望老是定时地暂停算法来计算一遍这个求和,因为这个求和计算需要考虑整个的训练集而随机梯度下降的算法是每次只考虑一个样本然后就立刻进步一点点,因此对于随机梯度下降算法为了检查算法是否收敛我们可以进行下面的工作:让我们沿用之前定义的cost函数:
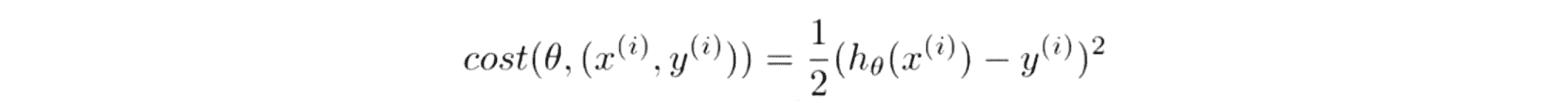
其计算方法就是关于θ的cost函数,其值等于二分之一倍的训练误差的平方和,然后在随机梯度下降法学习时,我们对某一个样本进行训练前在随机梯度下降中,我们要关注样本(x(i),y(i)) 然后关于这个样本更新一小步进步一点点然后再转向下一个样本 (x(i+1),y(i+1))。随机梯度下降就是这样进行的在算法扫描到样本(x(i),y(i)) 但在更新参数θ之前,我们使用这个样本可以算出这个样本对应的cost函数,我们要在更新θ前来完成这一步原因是如果我们用这个样本更新θ以后再让它在这个训练样本上预测其表现就比实际上要更好了。最后为了检查随机梯度下降的收敛性我们要做的是每1000次迭代就画出前一步中计算出的cost函数,我们把这些cost函数画出来并对算法处理的最后1000个样本的cost值求平均值。如果我们这样做的话它会很有效地帮你估计出我们的算法在最后1000个样本上的表现。所以我们不需要时不时地计算总的 Jtrain 那样的话需要所有的训练样本,随机梯度下降法的这个步骤只需要在每次更新θ之前进行也并不需要太大的计算量,要做的就是每1000次迭代运算中我们对最后1000个样本的cost值求平均然后画出来,通过观察这些画出来的图我们就能检查出随机梯度下降是否在收敛。
下面几幅画出来的图的例子,假如你已经画出了每1000组样本的cost函数的平均值:

由于它们都只是1000组样本的平均值,因此它们看起来有一点嘈杂,因此cost的值不会在每一个迭代中都下降。假如我们得到一种这样的图像看起来是有噪声的,但我们应该判断这个算法总体来说是在下降的,这基本说明你的学习算法是渐渐收敛的。如果我们想试试更小的学习速率,那么你很有可能看到的是算法的学习变得更慢了因此代价函数的下降也变慢了,但由于你使用了更小的学习速率我们很有可能会让算法收敛到一个好一点的解,下图中红色的曲线代表随机梯度下降使用一个更小的学习速率:

出现这种情况是因为随机梯度下降不是直接收敛到全局最小值而是在局部最小附近反复振荡,所以使用一个更小的学习速率最终的振荡就会更小。有时候这一点小的区别可以忽略,但有时候一点小的区别,我们就会得到更好一点的参数。
接下来再看几种其他的情况。假如我们还是运行随机梯度下降然后对每1000组样本取cost函数的平均值并且画出图像那么下图另一种可能的图形:

看起来这样还是已经收敛了,如果我们把这个数 1000 提高到5000组样本,那么可能会得到一条更平滑的曲线:

通过在5000个样本中求平均值我们会得到比刚才1000组样本更平滑的曲线,这是我们增大平均的训练样本数的情形。当然增大它的缺点就是现在每5000个样本才能得到一个数据点,因此我们所得到的关于学习算法表现的反馈就显得有一些“延迟”。
沿着相似的脉络有时候我们运行梯度下降可能也会得到下面这样的图像:

如果出现这种情况我们要知道可能我们的代价函数就没有在减小了,也就是说算法没有很好地学习因为这看起来一直比较平坦代价项并没有下降。但同样地如果你对这种情况时也用更大量的样本进行平均,我们很可能会观察到红线所示的情况:

能看得出,实际上代价函数是在下降的只不过蓝线用来平均的样本数量太小了嘈杂让我们看不出来代价函数的趋势确实是下降的,所以可能用5000组样本来平均比用1000组样本来平均更能看出趋势。即使如此我们还是可能会发现这条学习曲线还是比较平坦,即使我们用更多的训练样本。如果是这样的话那可能就更肯定地说明不知道出于什么原因算法确实没怎么学习好,那么我们就需要调整学习速率或者改变特征变量或者改变其他的什么。
最后一种我们可能会遇到的情况是如果我们画出曲线,我们会发现曲线实际上是在上升的:

这是一个很明显的信号告诉我们算法正在发散,那么我们要做的事就是用一个更小一点的学习速率α。
好的希望通过这几幅图能让你了解到当画出cost函数在某个范围的训练样本中求平均值时各种可能出现的现象,也告诉你在遇到不同的情况时应该采取怎样的措施。比如如果曲线看起来噪声较大或者老是上下振动,那就应该试试增大平均的样本数量这样应该就能得到比较好的变化趋势;如果发现代价值在上升那么就换一个小一点的α值。
最后还需要再说一下关于学习速率的问题,我们已经知道 当运行随机梯度下降时算法会从某个点开始然后曲折地逼近最小值,但它不会真的收敛而是一直在最小值附近徘徊,因此我们最终得到的参数实际上只是接近全局最小值而不是真正的全局最小值:

在大多数随机梯度下降法的典型应用中,学习速率α一般是保持不变的,因此假如我们的数据和出发点如下:
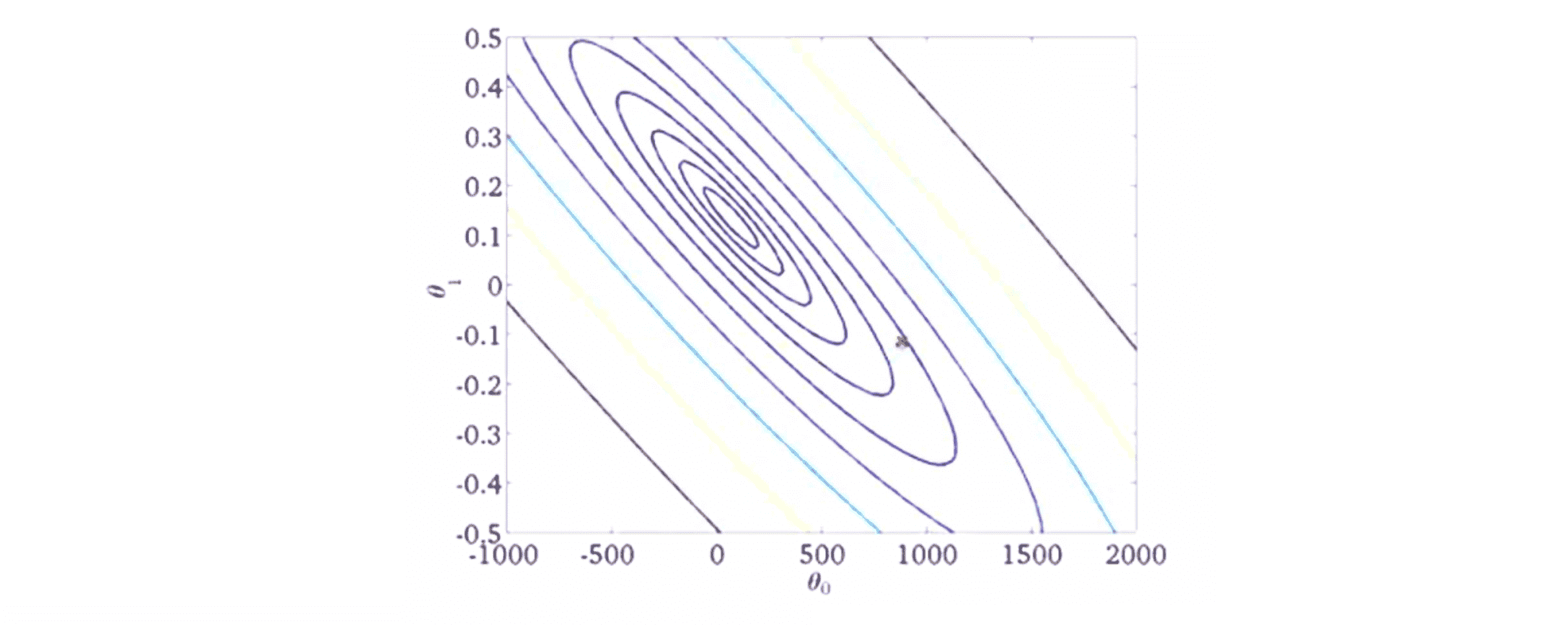
我们最终得到的结果一般来说是这个样子的:
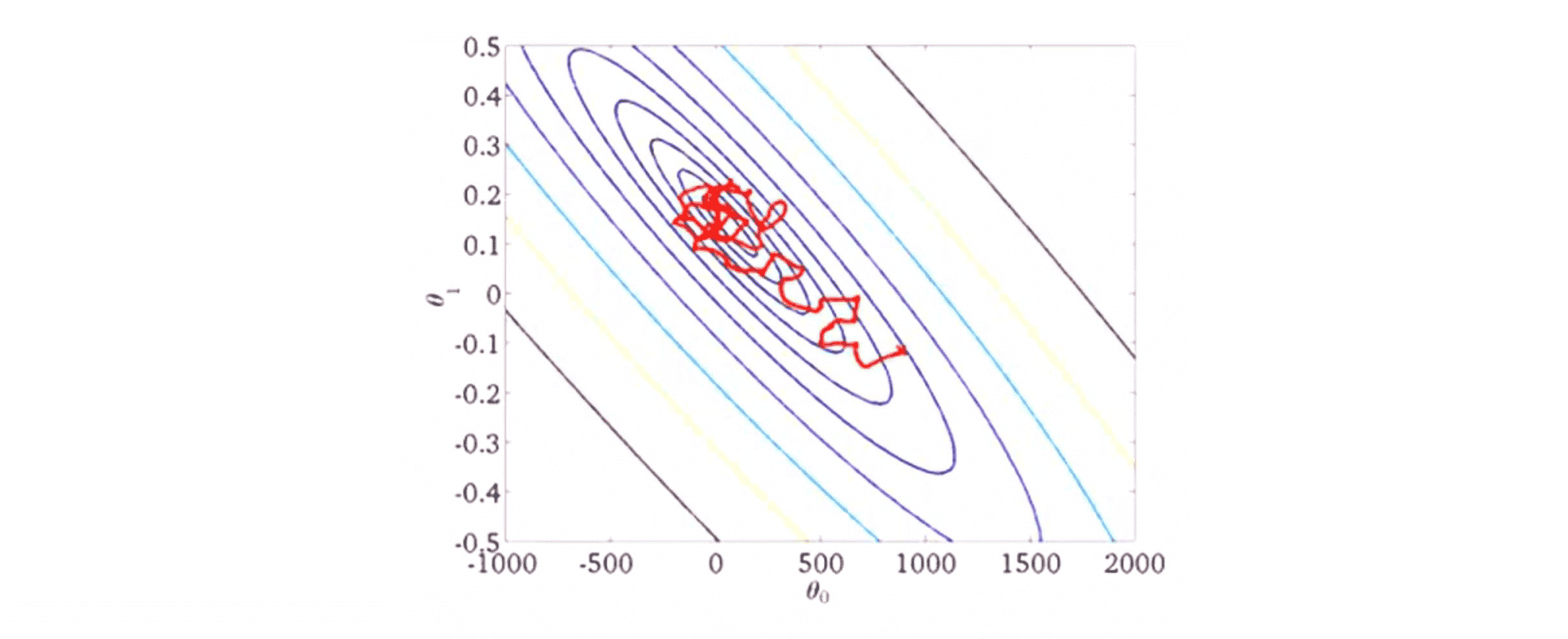
如果我们想让随机梯度下降确实收敛到全局最小值,我们可以随时间的变化减小学习速率α的值,其中一种典型的方法来设置α的值为下式子:

我们让α等于某个常数除以迭代次数加另一个常数。迭代次数指的是我们运行随机梯度下降的迭代次数就是你算过的训练样本的数量,两个常数是两个额外的参数我们需要选择一下才能得到较好的表现。但很多人不愿意用这个办法的原因是我们最后会把问题落实到把时间花在确定常数1和常数2这两个常数上,这让算法显得更繁琐。也就是说为了让算法更好我们要调整更多的参数。但如果你能调整得到比较好的参数的话我们会得到的图形是我们的算法会在最小值附近振荡但当它越来越靠近最小值的时候由于我们减小了学习速率,因此这个振荡也会越来越小直到落到几乎靠近全局最小的地方:
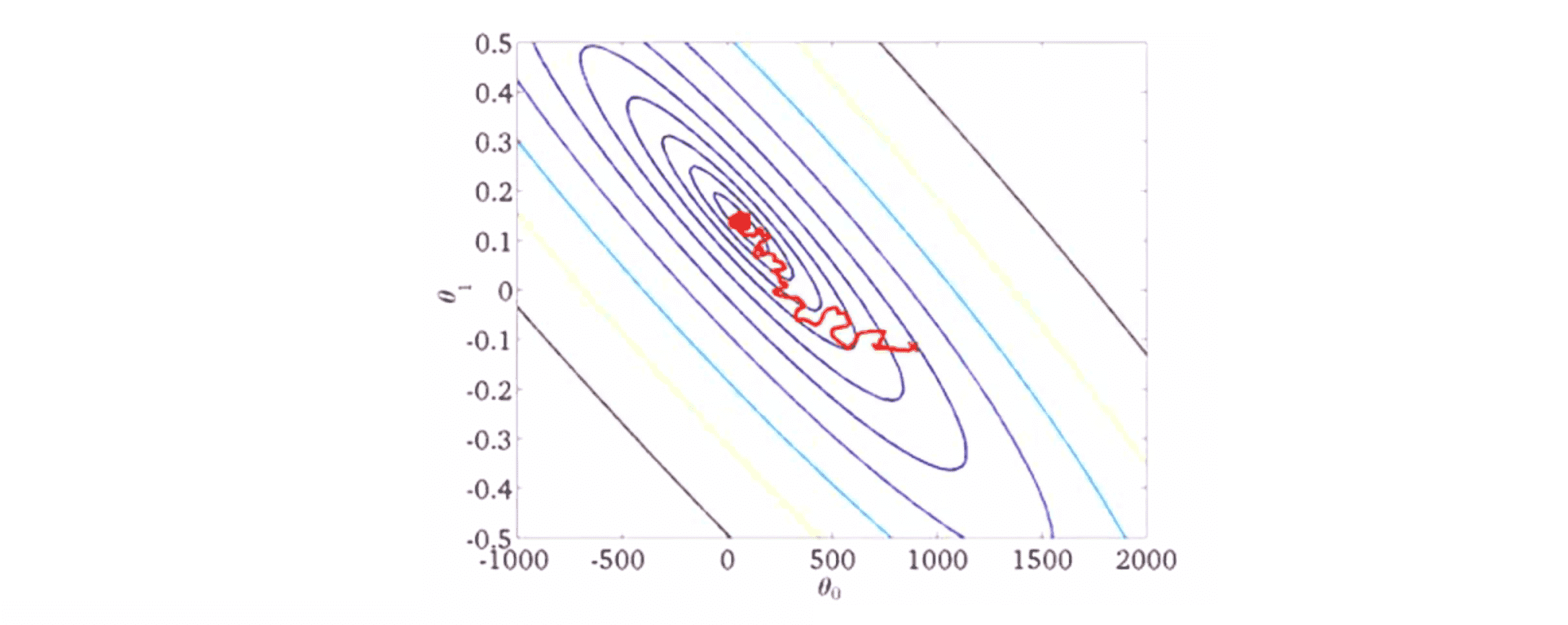
所以这个公式起作用的原因是随着算法的运行迭代次数会越来越大因此学习速率α会慢慢变小,因此你的每一步就会越来越小直到最终收敛到全局最小值。所以如果我们慢慢减小α的值到0我们会最后得到一个更好一点的假设。但由于确定这两个常数需要更多的工作量并且我们通常也对能够很接近全局最小值的参数已经很满意了,因此我们很少采用逐渐减小α的值的方法。在随机梯度下降中我们看到更多的还是让α的值为常数,虽然两种做法的人都有。
结语
通过这篇BLOG,相信你已经初步掌握了随机梯度下降算法的精髓。在下一篇BLOG我们将会将一些大数据下的其他机器学习算法。最后希望你喜欢这篇BLOG!