在之前的BLOG里,我们介绍了如何解决回归问题和回归问题,在这些问题中,我们可能会出现欠拟合过拟合等各种问题。这篇BLOG,就让我们看看什么是欠拟合过拟合问题以及如何用正则化去解决它们。
过度拟合
到现在为止我们已经学习了几种不同的学习算法模型,比如线性回归和逻辑回归。它们能够有效地解决许多问题,但是当将它们应用到某些特定的机器学习问题时,可能会遇到过度拟合(over-fitting)的问题,这可能会导致它们效果很差。
什么是过度拟合问题呢?让我们继续使用那个用线性回归来预测房价的例子,我们通过建立以住房面积为自变量的函数来预测房价。我们可以对我们的数据集做线性回归,如果这么做,我们就能拟合数据的这样一条直线:
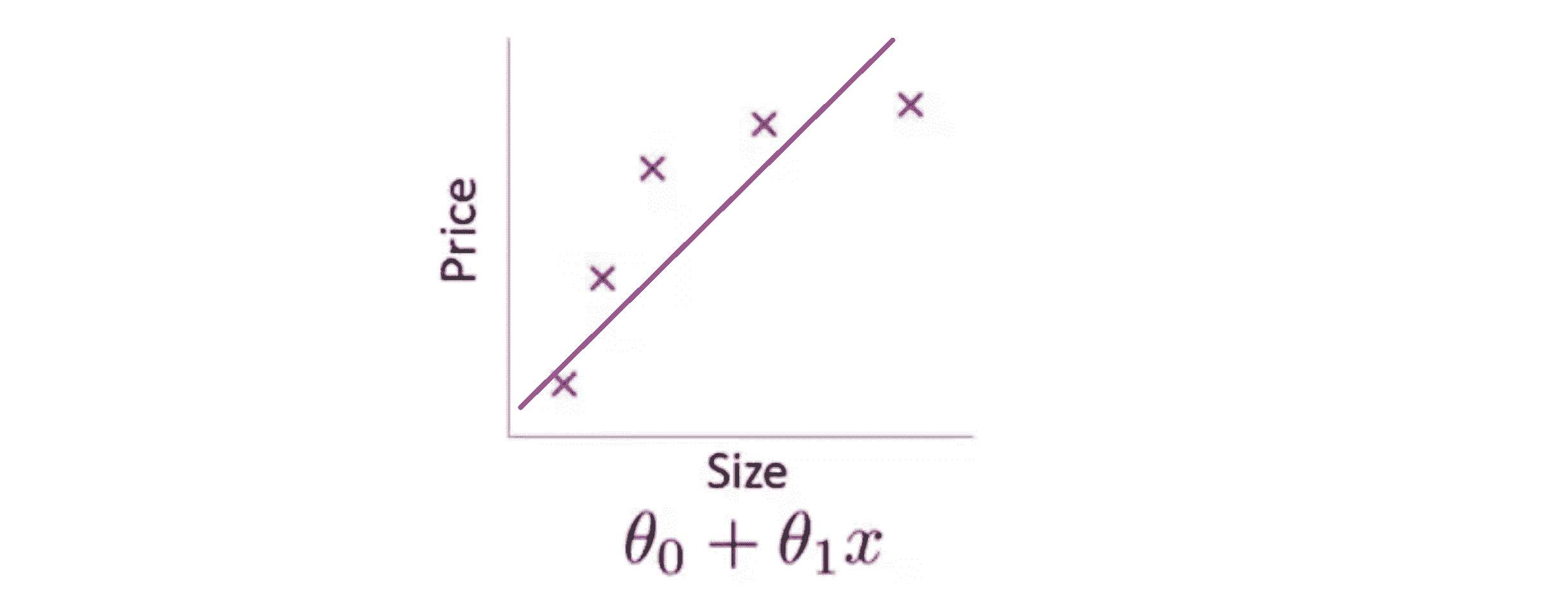
但是,这不是一个很好的模型,因为很明显,随着房子面积增大,住房价格的变化趋于稳定,换句话说就是越往右越平缓,因此该算法没有很好拟合训练数据。我们把这个问题称为欠拟合(underfitting) 或者高偏差(high bias),意思是我们的方程没有很好地拟合训练数据。
我们现在可以在中间加入一个二次项,用二次函数来拟合它,然后我们可以拟合出一条曲线:
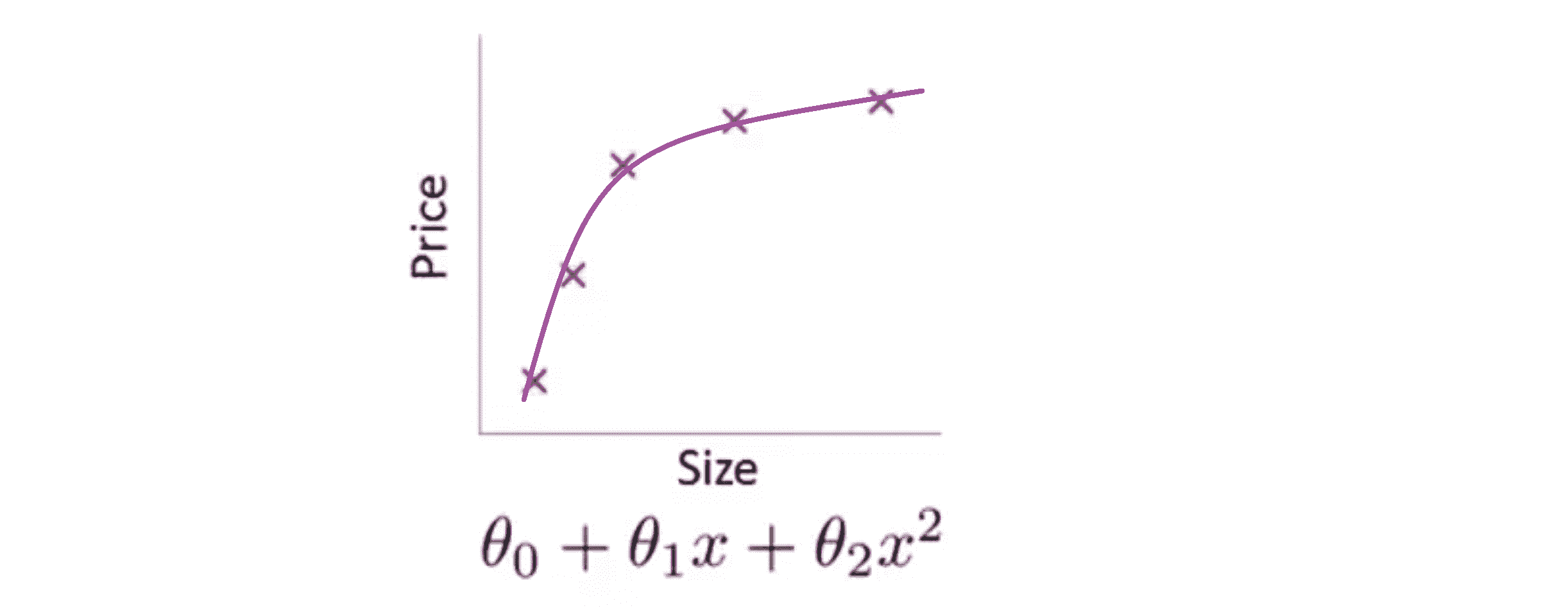
事实证明这个拟合效果是比较好的。
另一种情况是,如果我们拟合一个四次多项式所代表的一条曲线,通过我们的五个训练样本,我们可能会得到下图这样的一条曲线 :
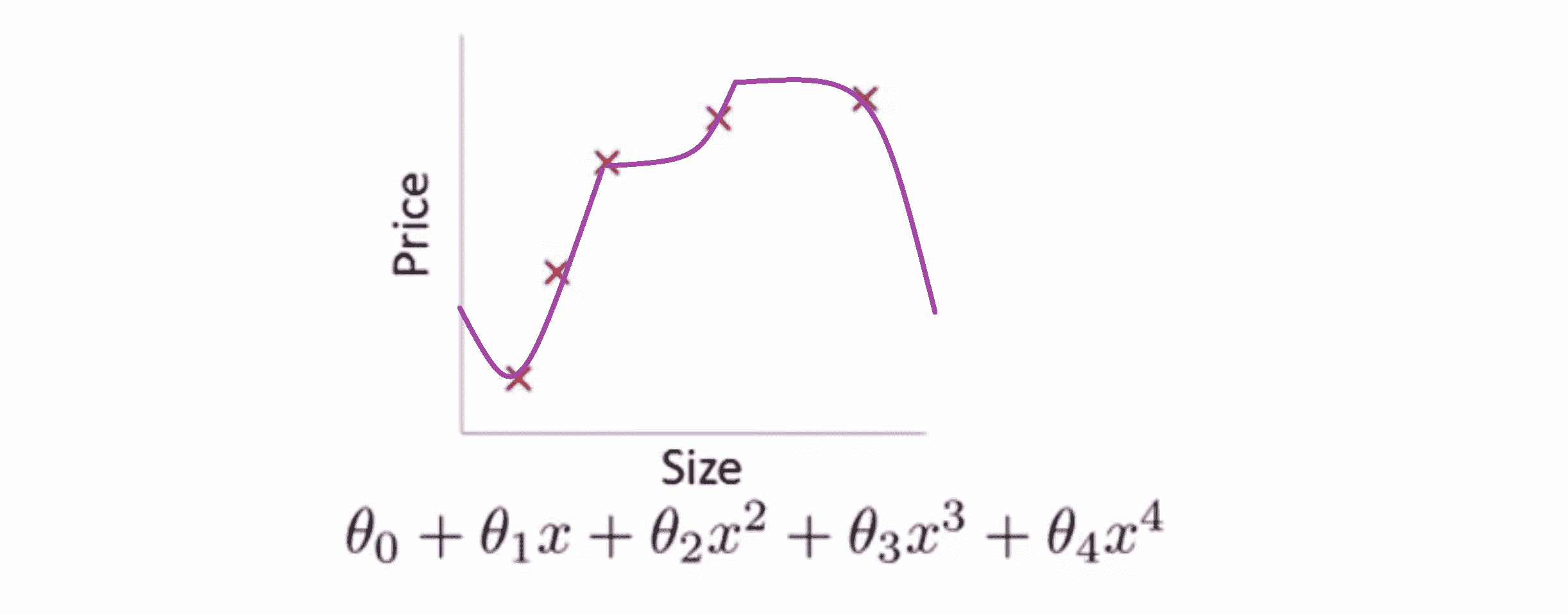
虽然我们的曲线对所有训练数据做了一个很好的拟合,它通过了所有的训练实例,但是这得到的是一条扭曲的曲线,它不停上下波动,因此我们并不认为它是一个预测房价的好模型。所以这个问题我们把他叫做过度拟合或过拟合(overfitting) 或者高方差(high variance)。
如果我们用数据去拟合一个高阶多项式,那一般得到的函数都能很好的拟合训练集,能拟合几乎所有的训练数据。这就面临可能函数太过庞大的问题,如果变量太多同时如果我们没有足够的数据去约束这个变量过多的模型,那么我们就可能过度拟合。
总而言之,过度拟合的问题将会在变量过多或者次数过高的时候发生,这种时候训练出的方程总能很好的拟合训练数据,所以我们的代价函数实际上可能非常接近于0:
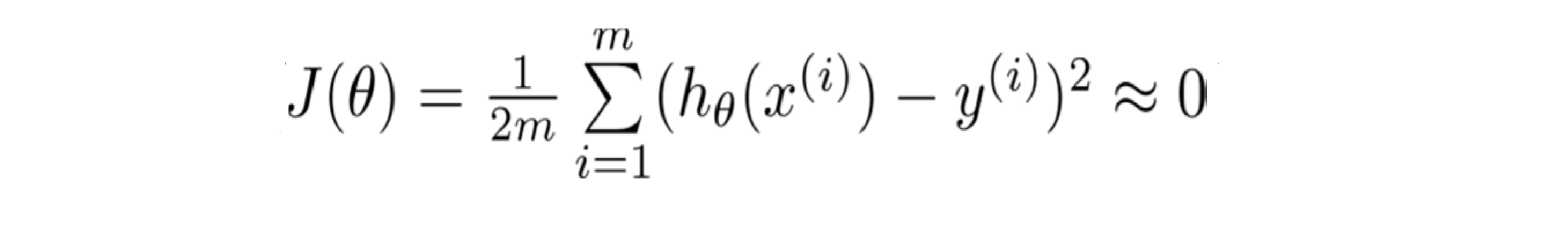
但是这样的曲线,它千方百计的拟合于训练数据这样导致它无法泛化到新的数据样本中,以至于无法预测新样本价格。在这里"泛化"指的是一个假设模型能够应用到新样本的能力;而新样本数据指的是没有出现在训练集中的样本。
上面的内容让我们看到了可能发生在回归问题中的过度拟合,而分类问题也可能出现在分类问题上。
我们还以举肿瘤分类的例子把,其是一个以 x1 与 x2 为变量的逻辑回归。假设我们有一个数据集,我们用线性的假设模型来作为分类器,结果可能如下:
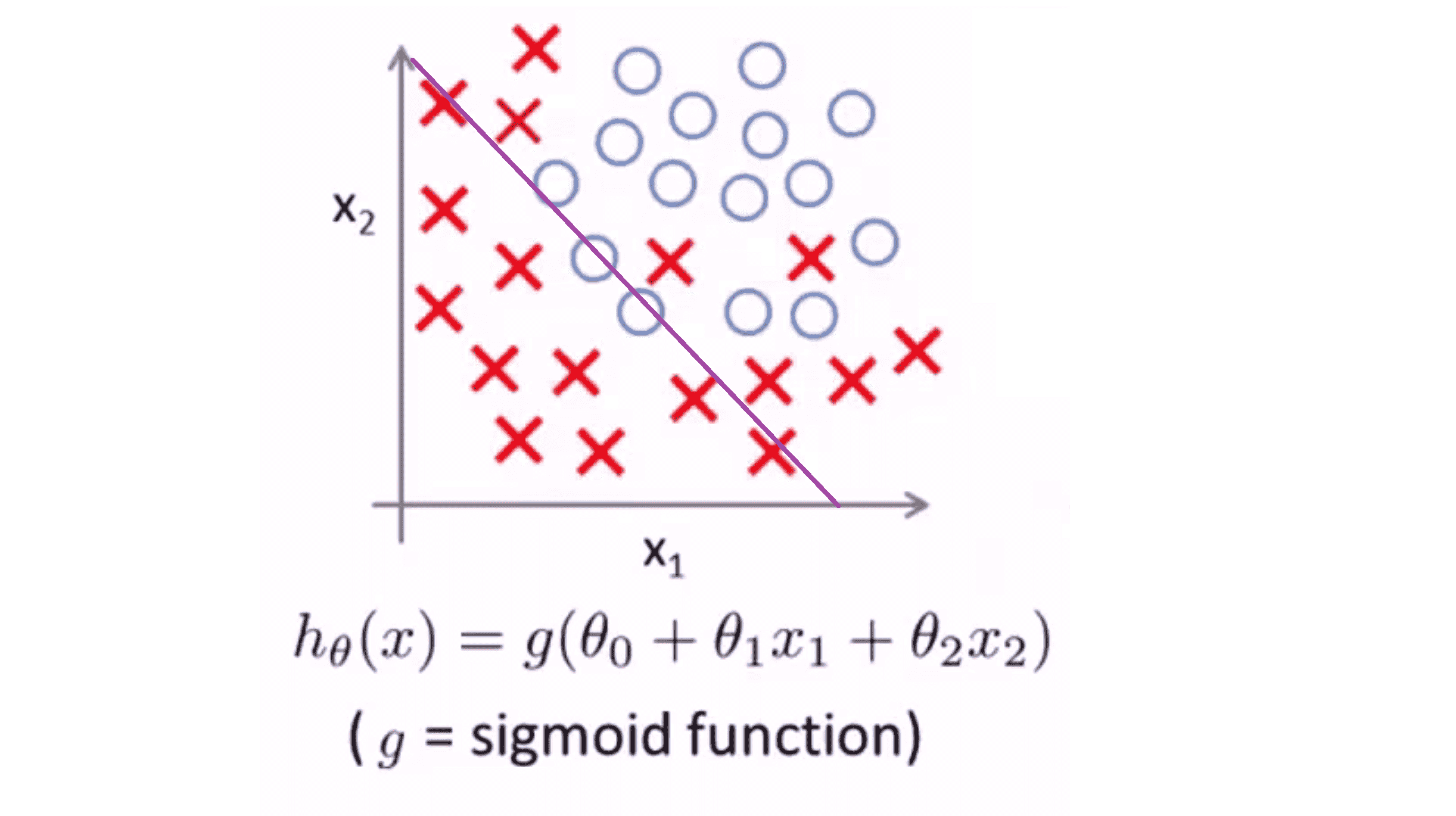
这个假设模型是一条直线,它大致分开了正样本和负样本,但这个模型并不能够很好的拟合数据。因此这又是一个欠拟合的例子,或者说假设模型具有高偏差。
相比之下如果我们再加入一些变量,比如二次项,那么我们可能会得到下面这样一个判定边界:
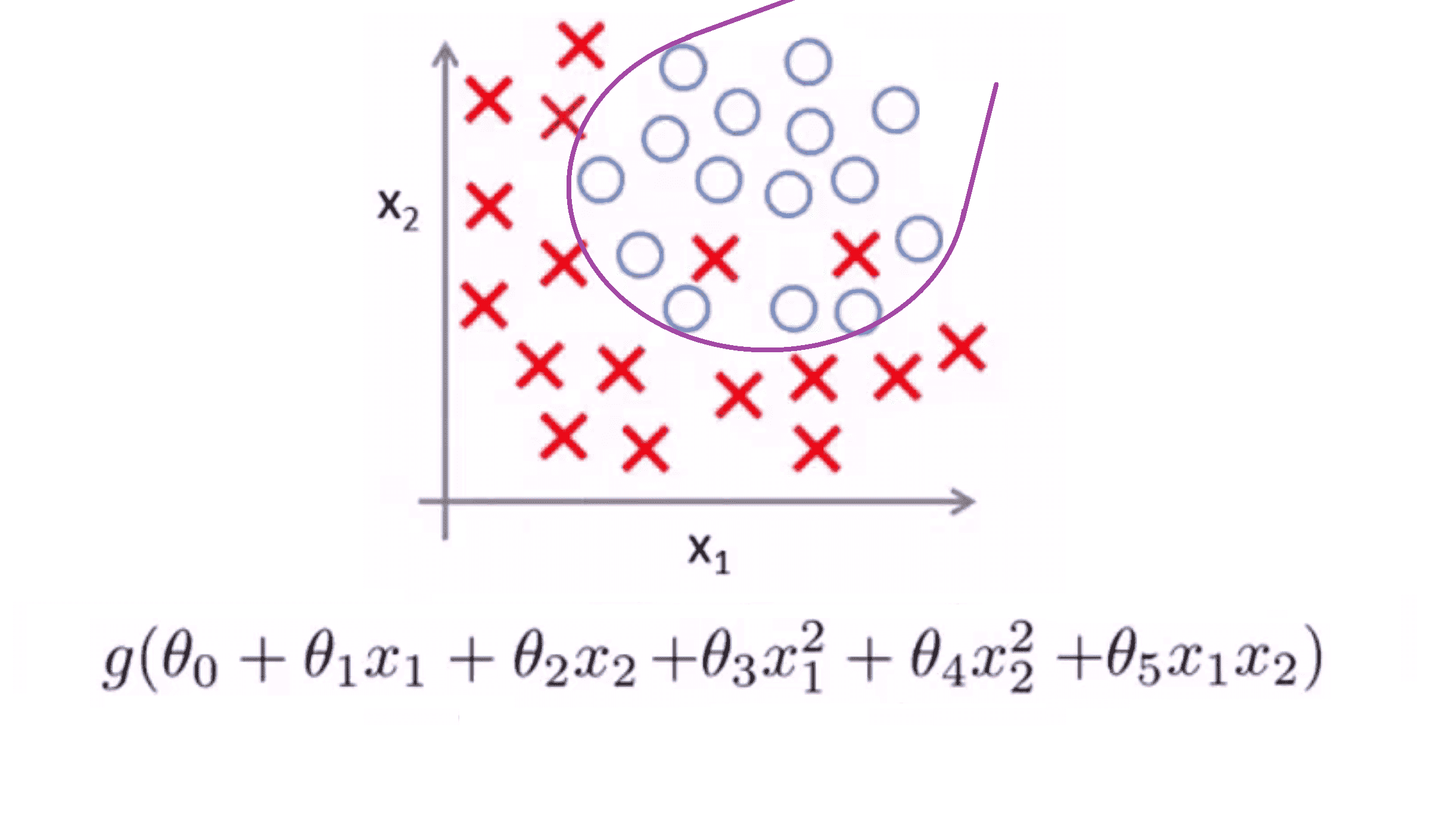
这样就很好的拟合了数据,且很可能是训练集的最好拟合结果。
但是在另一种极端情况下,如果我们用高阶多项式来拟合数据,那么逻辑回归可能发生自身扭曲:
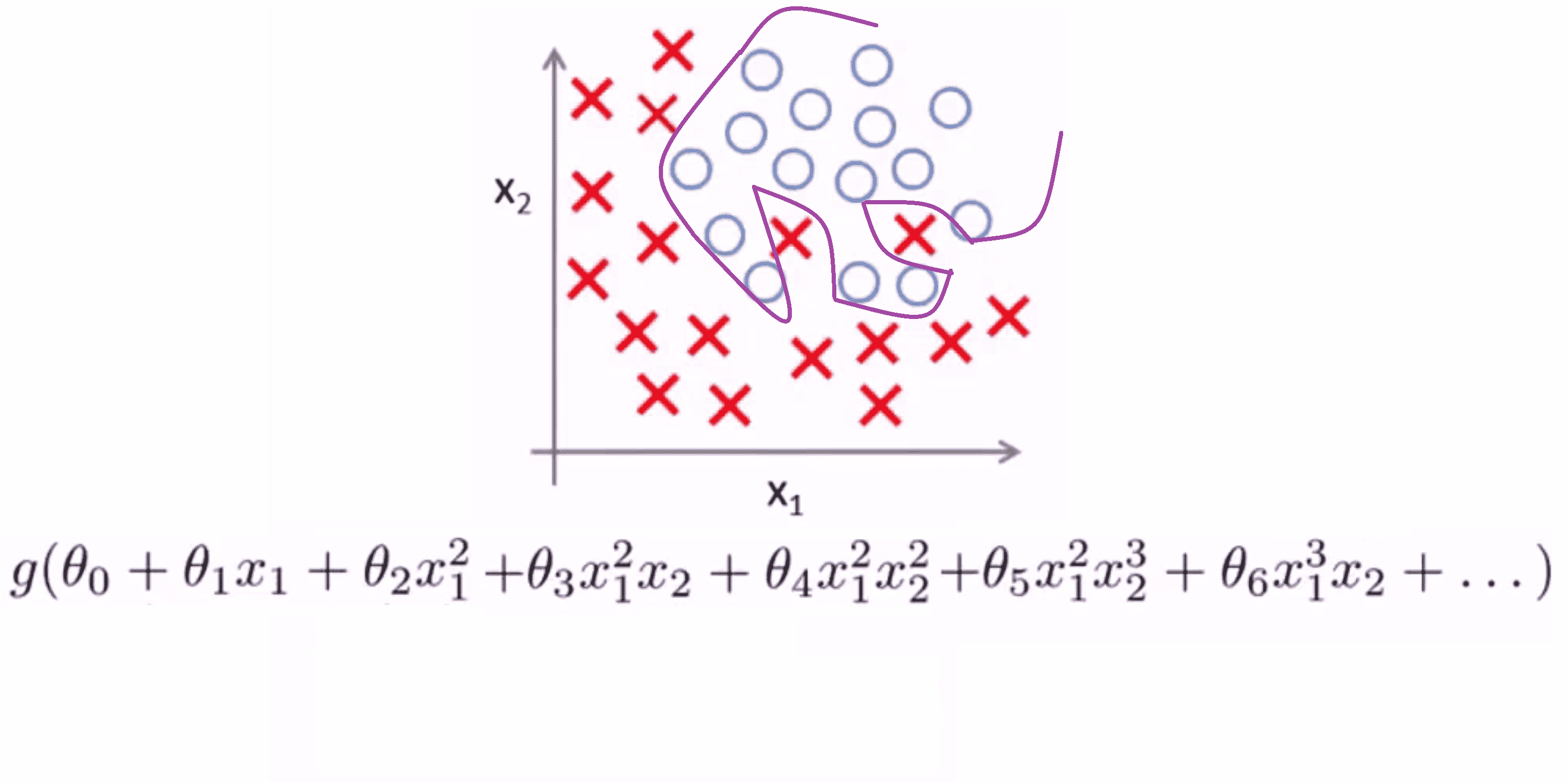
它千方百计地形成这样一个判定边界来拟合我们所有的训练数据,以至于成为一条扭曲的曲线,使其能够拟合每一个训练集中的样本,但这个假设模型确实不是一个很好的预测。因此这又是一个过拟合例子,换句话说是一个有高方差的假设模型,并且不能够很好泛化到新样本。
过度拟合的解决方法
现在让我们来看看过拟合的问题是怎么样解决呢。在之前的BLOG中,我们提到过当使用一维或二维数据时,我们可以通过绘出假设模型的图像来研究问题所在,再选择合适的多项式来拟合数据。因此以之前的房屋价格为例,我们只要绘制出绘制假设模型的图像,就能看到模型的扭曲的曲线,来选择合适的多项式阶次:
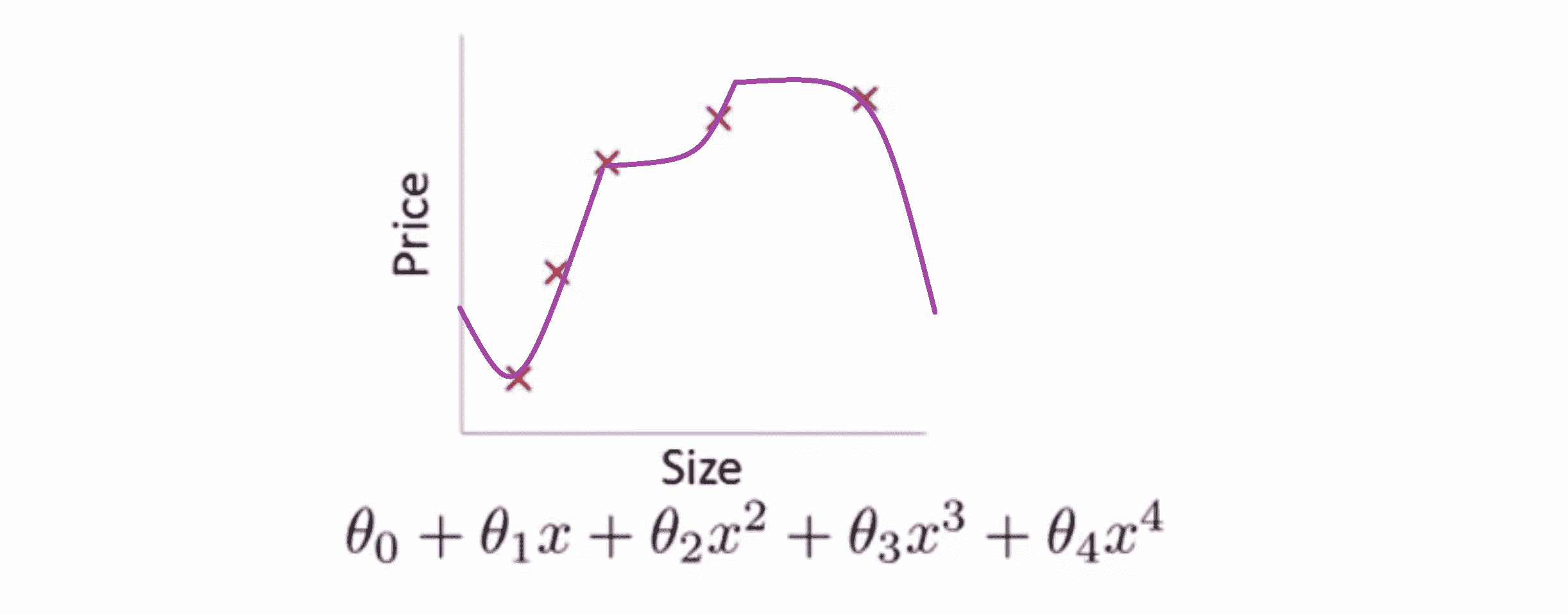
因此绘制假设模型曲线可以作为决定多项式阶次的一种方法,但是这并不是总是有用的,因为事实上更多的时候我们会遇到有很多变量的假设模型,这不仅仅是选择多项式阶次的问题,太多的特征变量也使得绘图变得更难,因此并不能通过绘图这种方法决定保留哪些特征变量。
具体地说如果我们试图预测房价,同时又拥有非常多的特征变量,比如:

这些变量看上去都很有用,但是过多的变量和非常少的训练数据,就可能导致过度拟合的问题。为了解决过度拟合,我们一般有两种常用的办法。
第一个办法是要尽量减少选取变量的数量。具体而言我们可以人工检查变量,并决定哪些变量更为重要,然后决定保留哪些特征变量,舍去剩余的变量。在今后的学习中,我们会学习到模型选择算法,这种算法能够自动选择采用哪些特征变量,并自动舍弃不需要的变量。这种减少特征变量的做法是非常有效的,并且可以减少过拟合的发生。但是其缺点是我们舍弃一部分特征变量,也舍弃了问题中的一些信息。例如也许所有的特征变量对于预测房价都是有用的,我们实际上并不想舍弃一些信息或者舍弃这些特征变量。
为了解决上一方法的缺点,我们就有了第二个方法-正则化。正则化中我们将保留所有的特征变量,但是却能解决过拟合问题,所以下一部分,就让我们来看看正则化具体是怎么操作的。
正则化
在这一部分,我们将通过一些直观的感受,来学习你正规化是如何进行的。在前面的部分中我们看到了,还是对于那个卖房的数据集,如果说我们用一个二次函数来拟合数据集,则我们可以得到一个对数据比较好的拟合,然而如果我们用一个更高次的多项式去拟合,最终就可能得到一个能非常好地拟合训练集但过度拟合了的曲线:
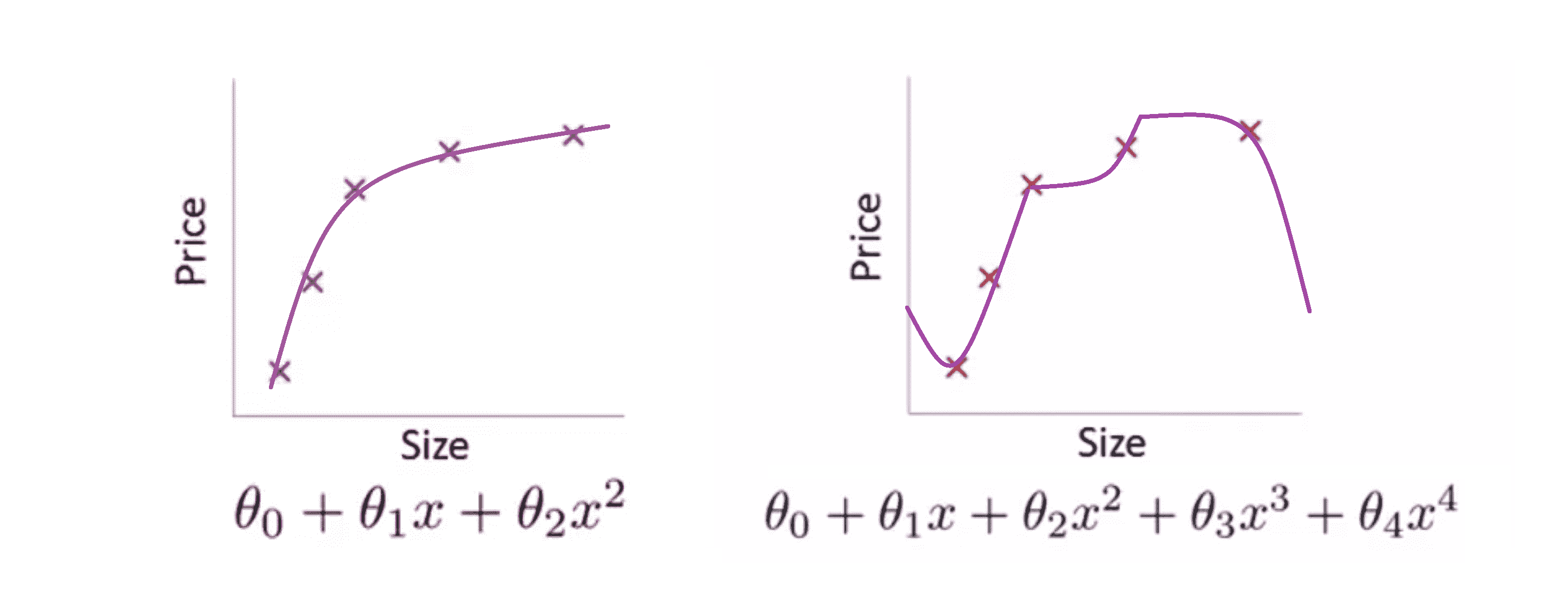
让我们看高次拟合的这个例子,为了减少我们高次项的系数,现在我们考虑加上惩罚项,来让参数 θ3 和 θ4 足够的小,而这就是我们需要优化的问题。我们尝试修改我们的代价函数。对于代价函数,我们给它添加一些项,比如加上 1000 θ3^2 再加上 1000 θ4 ^2。 1000 只是随便写的某个较大的数字而已,其具体数字是多少不是很重要:
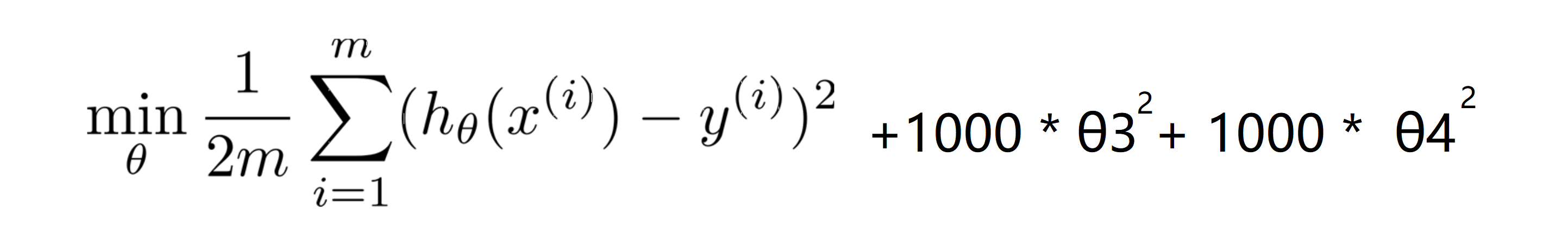
现在为了使这个新的代价函数最小化,我们就要让 θ3 和 θ4 尽可能小,因为如果你有 1000 θ3^2 + 1000 θ4 ^2 ,如果 θ3 和 θ4 比较大那么新的代价函数将会是很大的。所以当我们最小化这个新的函数时,这个添加的项将使 θ3 的值接近于0,θ4 的值也接近于0,就像我们忽略了这两个值一样。如果我们做到这一点 如果那么我们将得到一个近似的二次函数,其恰当地拟合了数据 :
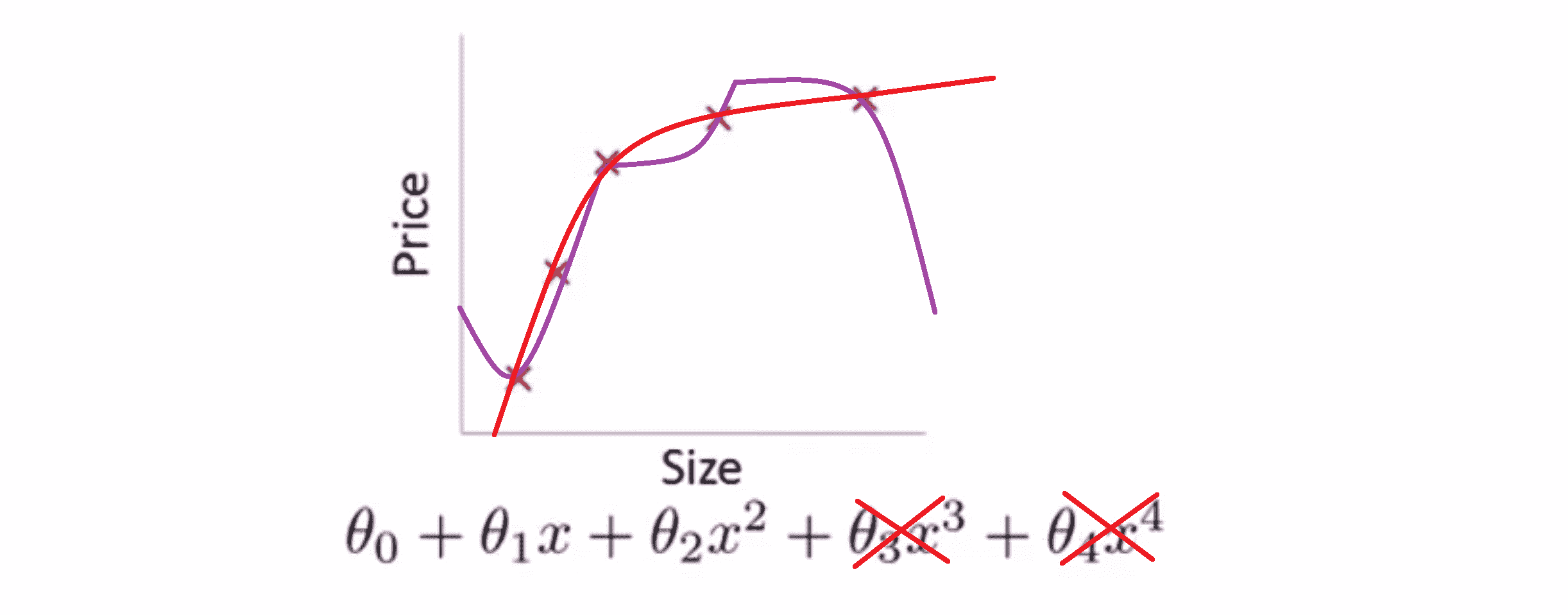
在上面这个具体的例子中,我们看到了惩罚这两个次数大的参数值的效果;更一般地,这里给出了正规化背后的思路,这种思路就是如果我们主要的参数值对应的都是较低次数项的话,那么往往我们会得到一个形式比较简单的假设。所以 我们上一个例子中,我们惩罚的只是高次项对应的系数 θ3 和 θ4 ,其我们得到了一个更简单的假设。
再让我们看看另一个例子,仍然是对于房屋价格预测。我们可能有上百种特征:

如果我们有一百个特征,我们是很难提前选出那些关联性比较小的特征值的,且也很难看到什么是高次项还是低次项,因为它们看起来好像都是一样的,因此在正规化里我们要做的事情就是尝试修改我们的代价函数从而缩小我所有的参数值。
因为在这个问题中我们不知道是哪个哪一个或两个参数要去缩小,所以我就尝试去缩小每个参数,即代价函数如下:
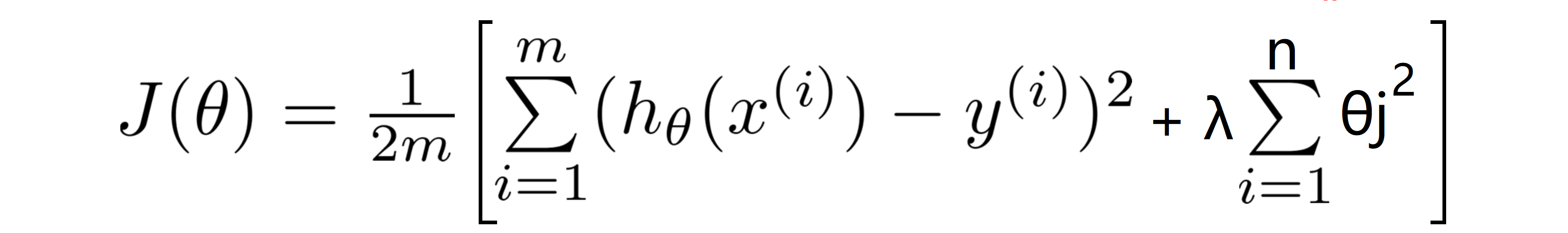
按照惯例来讲,我们的惩罚从θ1开始,所以我们实际上没有去惩罚 θ0,因此 θ0 的值是大的,这就是一个通俗的约定。惩罚从 θ1 到 θn 求和,而不是从 θ0 到 θn 求和,但其实在实践中这两者只会有非常小的差异,但是按照惯例,我们通常情况下我们还是只 从 θ1 到 θn 进行正规化。
我们的正规化后的代价函数上图的 J(θ) 这个项,右边新添加的项就是一个正则化项,并且 λ 在这里被称做正规化参数, λ 要做的就是控制在两个不同的目标中的一个平衡关系:第一个目标是让假设更好地拟合训练数据,而第二个目标是想要保持参数值较小,从而来保持假设的形式相对简单,来避免过度的拟合。
对于我们之前的房屋价格预测的例子,尽管我们之前用非常高次的高阶多项式来拟合,得到一个非常弯曲和复杂的曲线函数,但使用了普通的正规化目标的方法后,即没有单独去惩罚某一项,而是去惩罚所有项的话,我们也会得到一条更加的流畅和简单,就像下图红色的曲线一样的曲线:
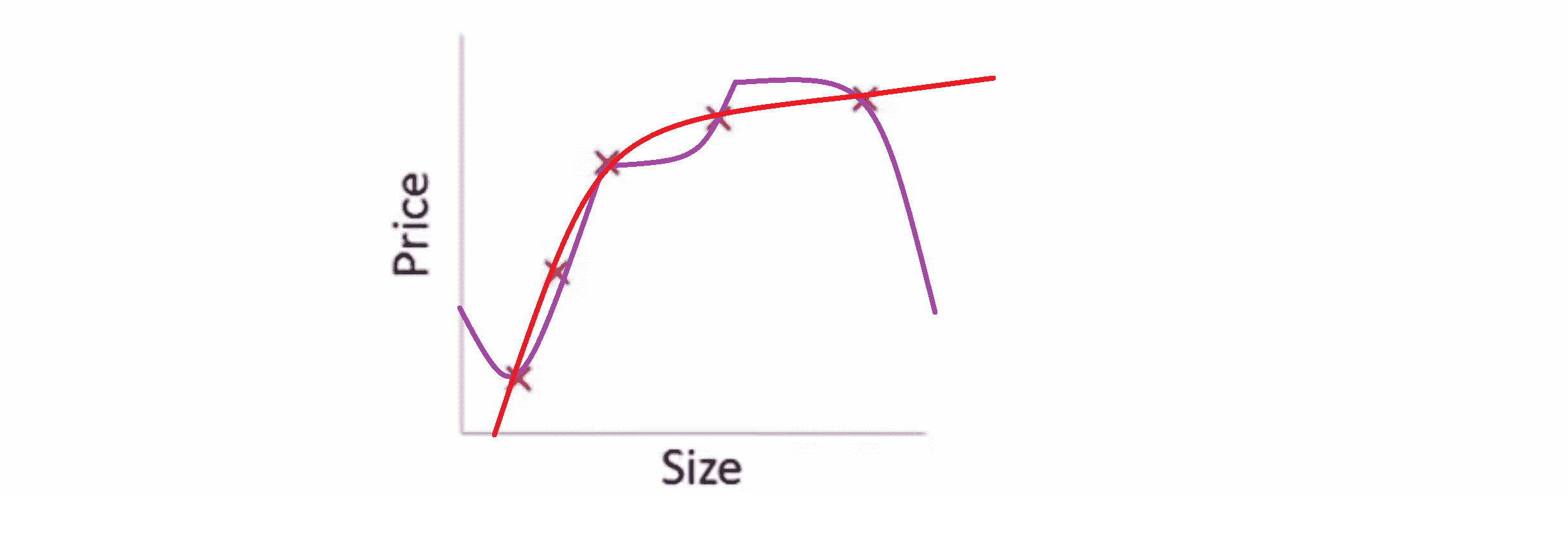
我了解这部分有点难以明白,为什么加上参数的影响可以产生这种效果,但如果你亲自实现了正规化,你将能够看到这种影响的最直观的感受。
我们来看另一个问题,如果在正规化线性回归中,正规化参数值 λ 被设定为非常大,那么将会发生什么呢?在这种情况下我们将会非常大地惩罚参数θ1 θ2 θ3 θ4 ……,也就是说, θ1 θ2 θ3 θ4 ……可能会接近于零;那么我们的假设中就相当于去掉了后面的那些项,只剩下一个常数项 θ0 ,那我们预测的房屋价格就一直等于 θ0 的值:
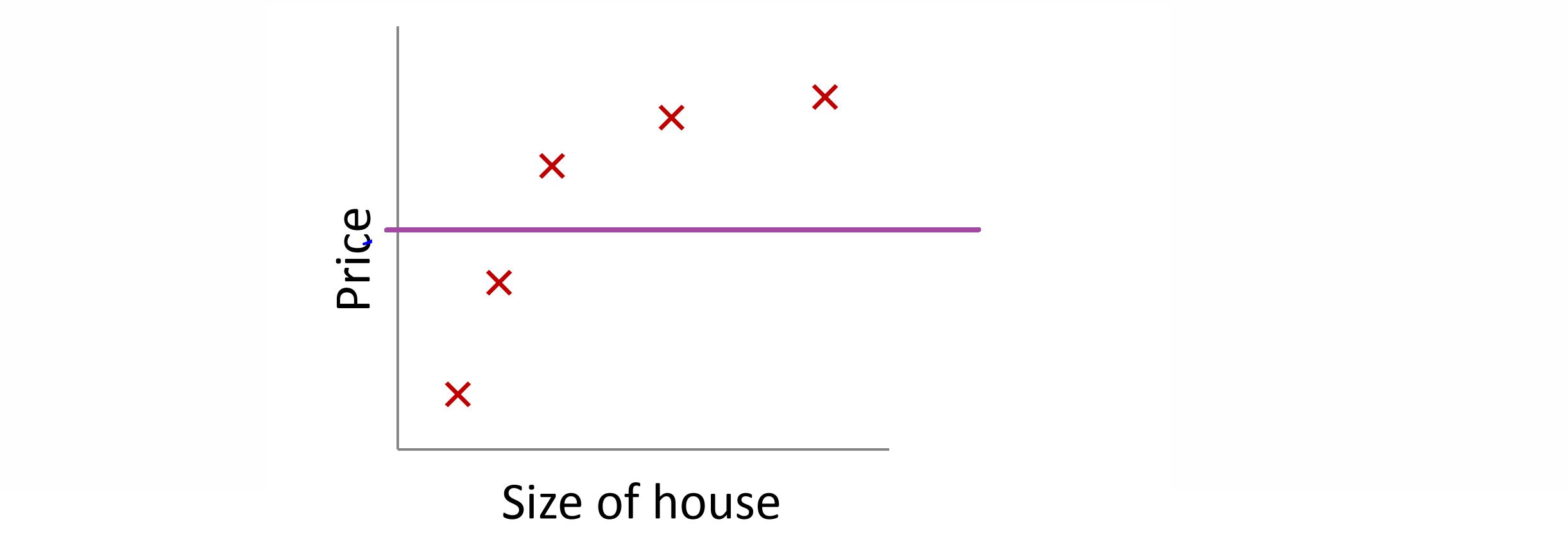
这就是类似于拟合了一条水平直线,对于数据来说这就是一个欠拟合 (underfitting) 的例子,对于训练集来说,这只是一条平滑直线它没有任何趋势,它也不会去趋向大部分训练样本的任何值,所以说这个假设有过高的偏差 (high bais),认为预测的价格只是等于 θ0 。
所以为了使正则化运作良好,我们应当注意一些方面,比如应该去选择一个恰当的正则化参数 λ ,在我们之后的学习中,我们将学习一系列的方法来自动选择正则化参数 λ 。
结语
通过这篇BLOG,相信你已经对过度拟合和正则化有了一定的认识。在之后的BLOG里,我们会具体介绍如何将正则化运用在我们已经学习过的学习算法中。最后希望你喜欢这篇BLOG!