在之前的BLOG中，我们学习了如何运用PCA进行降维。在这篇BLOG里，就让我们一同来看看PCA的几个应用吧！

压缩重现

在之前的BLOG我们一同学习了如何运用 PCA (主成分分析) 来进行压缩数据，我们现在能将高达一千维度的数据压缩到 只有一百个维度，或者将三维数据压缩到两个维度……那么按照道理来说如果有一个这样的压缩算法，那么也应该有一种方法可以从压缩过的数据近似地回到原始高维度的数据。假设有一个已经被压缩过的 z(i) 它有100个维度，怎样使它回到其最初的表示 x(i) 也就是压缩前的1000维的数据呢？这就是我们这一部分要解决的问题。

举个例子，在 PCA 算法中，我们一些二维的样本，我们使用 PCA 将这些样本投影在一维在平面上，现在我们只需要使用一个实数就将它们在这个一维平面z1上的位置明确地指定出来：

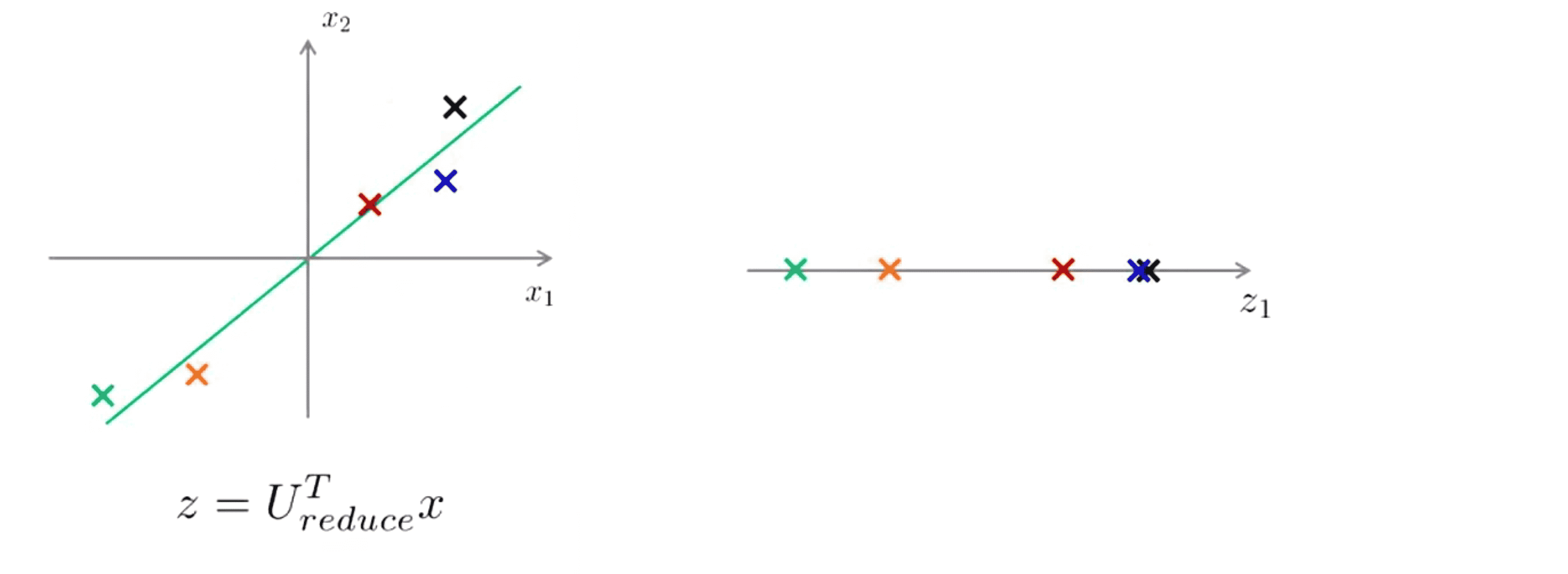
那现在任意给我们一个点我们如何重新得到原来的二维数据点呢？具体来说就是如果给出一个一维实数点 z 我们能否 让 z 重新变成原来的二维实数点x？

我们知道 z = Ureduce^T * x，那如果想得到相反的情形方程应这样变化 x_approx = Ureduce * z。我们检查一下维度，在这里 Ureduce 是一个n×k矩阵，z 就是一个k×1维向量，将它们相乘得到的就是n×1维，所以说 x_approx 是一个n维向量，这就是我们想要的。同时根据 PCA 的意图，投影的平方误差不能很大，也就是说 x_approx 将会与最开始用来导出 z 的原始 x。很接 用图表示出来大概就是这样：

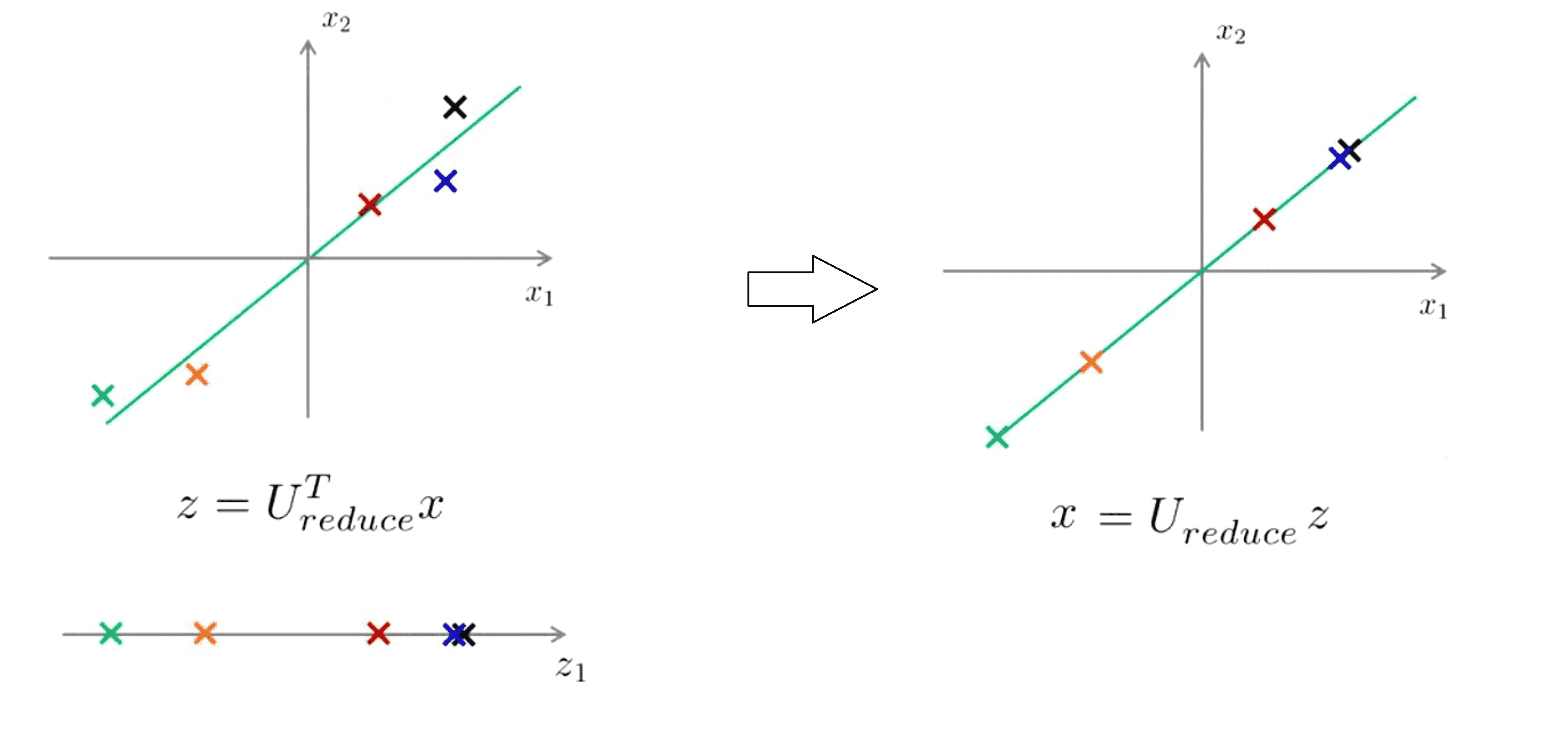
在这一过程后我们可以看到这些点都到绿线上去了。这就是用低维度的特征数据 z 回到未被压缩的特征数据，我们找到的是一个与原始数据x近似的x_apporx而不是完整的初始点，我们也称这一过程为原始数据的重构 ( reconstruction )，现在我们就可以在需要的时候从压缩过的数据重构出原始数据x了。

K的选择

在 PCA 算法中，我们把n维特征变量降维到k维特征变量。这个数字 k 是 PCA 算法的一个参数也被称作主成分的数量或者说是我们保留的主成分的数量，在大部分情况下都不是人为主动指定的。所以在这一部分中，我们就来看看如何自动选择 PCA 的参数 k 。

为了选择参数 k 也就是要选择主成分的数量，这里有几个有用的概念。 PCA 所做的是尽量最小化平均平方映射误差 (Average Squared Projection Error)， 因此 PCA 就是要将这个量最小化：

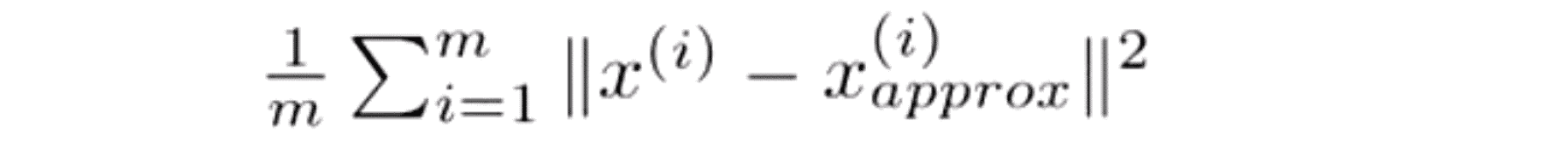
我们还要定义一下一个概念叫数据的总变差 (Total Variation)，其指的是这些样本 x(i) 的长度的平方的均值，也就是说 “平均来看 我的训练样本 距离零向量多远？” ：

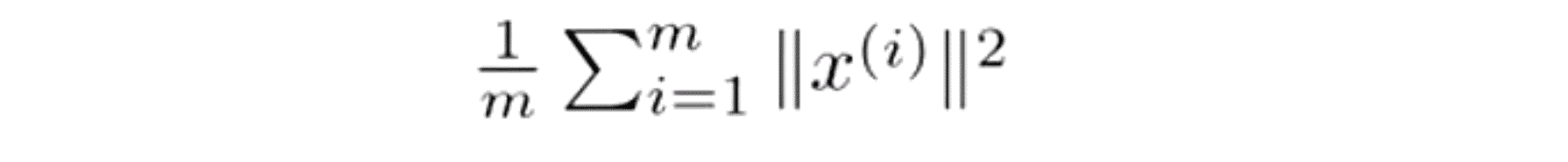
当我们去选择 k 值的时候 一个常见的选择K值的经验法则是选择能够使得它们之间的比例小于等于0.01的最小的k值：

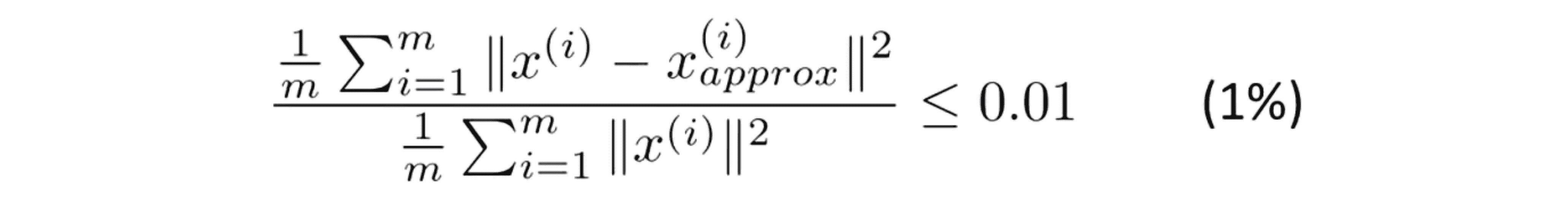
所以大部分人在考虑选择 k 的方法时，不是直接考虑选择多大的 k 值，而是考虑这个比值的上限应该是多少，它应该是 0.01 还是其它的数。如果是 0.01 用PCA的语言说就是保留了 99% 的差异性。因此如果你使用PCA并且你想要告诉别人你保留了多少个主成分，更为常见的一种说法是“我选择了参数k，使得99%的差异性得以保留” 。除了 0.01 另一个常用的值是0.05，如果是这样的话我们可以说 95%的差异性被保留了。

对于许多数据集，我们可能会惊讶就算保留99%的差异性通常还是可以大幅地降低数据的维度，这时因为大部分现实中的数据都是高度相关的。

那我们具体该如何实现它呢？你可能会从从 k=1 开始，然后我们再进行主成分分析我们算出 Ureduce z(1) z(2) …… z(m) 再算出所有那些 x_approx(1) …… x_approx(m) 然后我们看一下是否有 99% 的差异性是否被保留下来了：

是的话就搞定了我们就用 k=1；但如果不是那么我们接下来尝试 k=2 然后我们要重新走一遍这整个过程再检查是否满足这个表达的值小于0.01，如果不是我们再重复一次尝试 k=3 然后试 k=4 以此类推一直试到发现99%的数据差异性都被保留了我们才停下来，选择当前的 k 作为答案。

但是可以很清楚地看到这个过程的效率相当地低，幸好我们在应用 PCA 时，实际上可以利用svd分解出的另一个矩阵来使计算变得容易很多。让我们具体来看看，当我们调用 svd 来计算矩阵U S V时，我们除了得到矩阵 U 外，还会得到矩阵S，矩阵 S 是一个n×n 的正方形矩阵，更进一步它实际上是一个对角矩阵，其除了对角线上的元素 S11 S22 S33 …… Snn 外全部都是 0 ：

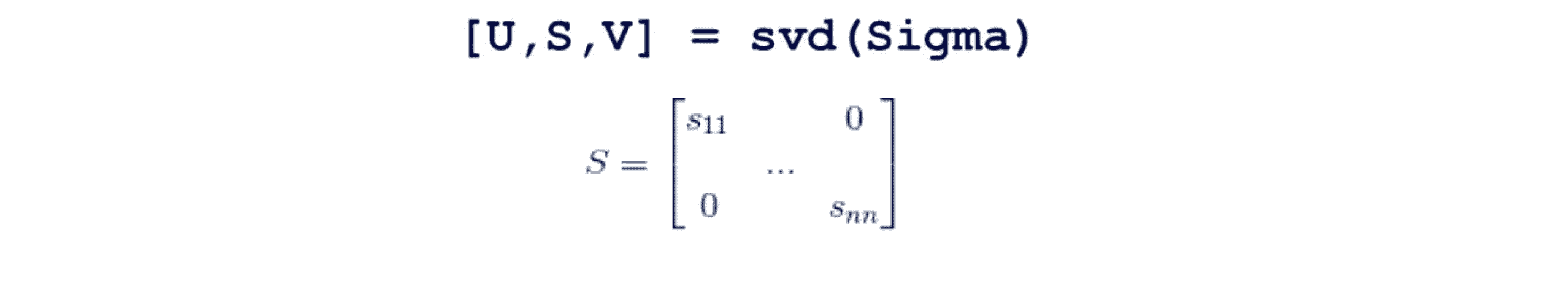
接着我们就可以利用矩阵 S 的对角线上的元素很轻易地计算出合适的 k 了。具体来说之前的那个表达式可以通过下面这个式子计算出来：

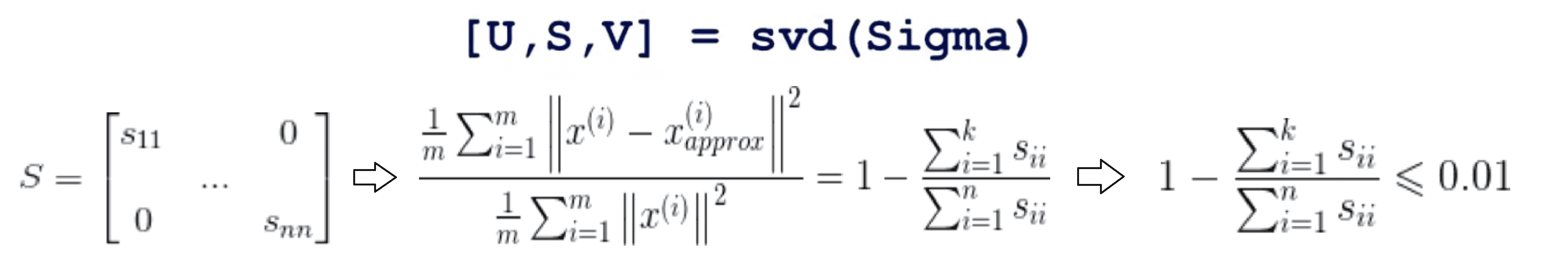
所以我们只要选取某个 k，看看1-对角线上前 k 个元素的和除于整个对角线上的元素的和是否小于等于0.01就可以了，这样就让计算量大大降低。或者等价的对角线上前 k 个元素的和除于整个对角线上的元素的和是否大于等于0.99：

如果我们想确保能够保留99%的差异性的话，我们就可以把k值设为1 2 3 ……慢慢增大以此类推并检验这个数值是否大于等于0.99即可。

这就是如何选择要将数据降低到什么维度，如果你将 PCA 应用于很高维的数据集，其常有较高的相关性，你经常会发现 PCA 在保留 99% 的差异性或者说 95% 的差异性或者某些高百分比的差异性，仍然能够非常有效地压缩数据。

运用建议

在这一部分，就让我们来看看一些应用 PCA 的建议吧。

运用场景

首先我们先来看看如何通过 PCA 来提高学习算法的速度。这种监督学习算法的提速，实际上也是很多人经常会通过使用 PCA 来实现的一种功能。比如说我们遇到了一个监督学习问题，注意这个监督学习算法问题有输入 x 和标签 y，假如说你的样本 x(i) 是非常高维的数据比如说 x(i) 是 一个 一张100 × 100的图片，就是一个10,000维的向量，那这样很高维的特征向量就会导致我们的监督学习算法运行会比较慢。幸运的是通过使用 PCA 我们能够降低数据的维数，从而使得算法能够更加高效地运行。

我们来看看具体的操作步骤：首先我们需要检查带标签的训练数据集并提取出输入数据，记住在这里我们只需要提取出 x 并暂时把 y 放在一边，这一步我们会得到一组无标签的训练集 x(1) …… x(m)，每个数据开始时都是 10,000维的向量。然后我们应用 PCA 对训练集进行降维，这就给了我们一个新的维数更小的训练集。在这之中假如之前我们有这样一个样本 （x(1), y(1)），降维后 x（1）就可以用 z(1) 来表示，这样我们就有了 一个新的训练集样本（x(2), y(1)）。同样地我们也有 （x(2), y(2)）……（x(m), y(m)）：

之后我们就可以将这个已经降维的数据集输入到逻辑回归算法或者是将其放入到神经网络中或者是SVM中，学习出假设 h。

最后如果我们有一个新的样本 x ，我们所要做的是将测试样本 x 通过同样的过程操作下来通过 PCA 你会得到所对应的 z ，然后将这个 z 值输入到得到的假设 h ，利用输出值对我们输入的 x 作出一个预测。

还有一点需要提醒，我们的 PCA 定义了从 x 到 z 的对应关系，这种从 x 到 z 的对应关系只可以通过在训练集上运行 PCA 定义出来而不能加上交叉验证集和测试集。具体来讲这种 PCA 所学习出的对应关系所做的就是计算出一系列的参数，比如特征缩放和均值归一化都是依据训练集的数据得出的。我们需要使我们的参数唯一地适应这些训练集而不是适应我们的交叉验证或者测试集，因此Ureduce矩阵中的数据就应该只通过对训练集运行PCA来获得。在训练集中找到了所有这些参数后，就可以将同样的对应关系应用到其他样本比如交叉验证数集样本或测试数据集当中了。

在之前的例子中，我们经常讨论将数据从上万维降到千维，但这实际上是并不切实际的，因为对于大多数我们实际面对的数据降维问题降维一般只能保证在降维到原来的五分之一或者十分之一依旧保持着原本维度数据的变化情况。就分类的精确度而言，数据降维后对学习算法几乎没有什么影响。如果我们将降维用在低维数据上，我们的学习算法会运行得更快。总之迄今为止我们讨论过的有关PCA的应用中第一个是数据压缩，我们可以借此减少内存或者磁盘空间的使用以存取更多的数据，接着就是使用数据压缩以加快学习算法。

在这些应用中为了选择一个k值，我们将会根据保留方差的百分比来确定 k 值，比如对于一个学习算法来说加快应用将会保留99%的方差或者说差异性；然而对于可视化应用来说，我们通常选择的K值要么等于2要么等于3，因为我们一般只去绘制出二维和三维的数据集。所以PCA的主要应用 需要对于不同的应用场景来选择K值。

误用场景

接着我们来看一看一个频繁被误用的PCA应用。你有时或许能听到其他人使用 PCA 来避免过拟合，当然这时错误的，下面是原因。

如果我们有有n个特征的数据集x(i)，如果我们将数据进行压缩并用压缩后的数据z(i)来代替原始数据，在降维过程中我们从n个特征降维到k个比先前的维度低看起来似乎更不容易过拟合，所以有些人认为 PCA 是一种避免过拟合的方法。 但我这里要强调一下 PCA 在过拟合问题上的应用是不合适的，不仅仅是因为这个方法的效果很差，还因为 PCA 把某些信息舍弃掉了。如果你比较担心过拟合问题，有更好的方法来解决那就是使用正则化方法代替 PCA 来对数据进行过拟合处理。原因是如果你仔细想想PCA是如何工作的，它并不需要使用数据的标签只需要处理输入数据 x(i) 来寻找更低维度的数据近似。但是在 PCA 的时候，我们一般保留数据99% 或者 95% 的方差，而过拟合本身就是高方差的问题，保留如此高比例的方差对于过拟合来说无疑是起不到什么作用的。

总之使用 PCA 的目的是加速学习算法，但是用它来避免过拟合却并不是一个好的PCA应用。最后讲一下PCA的滥用，PCA是一个非常有用的算法，很多人经常用它在可视化数据上进行数据压缩，但有时候会看到有些人把PCA用在了不应当使用的地方。从中有一个共同点：如果某人正在设计机器学习系统，他们或许会写下像这样的计划：

让我们设计一个学习系统得到训练集然后先运行PCA然后训练逻辑回归之后在测试数据上进行测试之类的。

通常在一个项目的初期有些人便直接写出项目计划并使用PCA。项目计划是非常好的问题是如果我们在整个项目中不加考虑直接使用PCA其实是不好的。通常人们不会去思考如果不用PCA会怎么样这个问题，尤其是当人们提出一个复杂的项目时，但实际上PCA舍去部分有用的信息可能会导致最后的效果差了那么一点点。所以我会建议大家在使用PCA之前思考清楚我们能否抛弃PCA这一步，并进一步思考我们如果试试在学习算法上使用原始数据效果会怎么样。

总之我不建议一开始不要将 PCA 方法就直接放到算法里，正确的步骤应该是先使用原始数据x(i)看看效果，当其中我们的学习算法收敛地非常缓慢或者占用内存或者硬盘空间非常大时，我们再去考虑用 PCA 来压缩数据。

尽管有这些需要注意的 PCA 仍旧是一种不可思议的有用的算法。希望你有能力实现 PCA 算法并用它来实现你的目的。

结语

通过这几篇BLOG，我们的PCA降维算法就告一段落了，相信你已经理解了如果善用PCA处理数据。最后希望你喜欢这篇BLOG!