在之前的BLOG里,我们多次提到数据规模对于机器学习算法的作用。数据规模越大训练出来的算法一定更加优秀吗?这篇BLOG就让我们一探究竟吧。
数据与算法效果
在之前的BLOG里。我曾告诫大家不要盲目地花大量的时间去收集大量的数据,因为数据不一定时时刻刻都能起到作用,比如当你的模型正在欠拟合的情况下。但是不得不承认,有时是唯一能实际起到改良算法作用的就是大量的数据。那么数据到底在学习算法的训练中起到了什么样的作用呢?
让我们先来看一个故事,很多很多年前,两位研究人员 Michele Banko 和 Eric Brill 进行了一项有趣的研究,他们的研究方向是不同训练数据集对不同的学习算法的效果 影响。他们当时考虑这样一个问题:如何在易混淆的词之间进行分类。比如在这样的句子中:For breakfast I at __eggs(to,two,too)。这就是一个易混淆的单词的例子。于是他们把诸如这样的机器学习问题当做一类监督学习问题,并尝试将其分类什么样的词在一个英文句子特定的位置 才是合适的。他们用了几种当时比较领先的学习算法:

第一种算法被称作"感知器" (perceptron),是用逻辑回归上的一个方差来进行拟合的算法;第二种算法是一种过去常用但是现在比较少用的算法- Winnow 算法,很类似于现在的回归算法但在一些方面又有所不同;第三种算法是一种基于内存的学习算法现在也用得比较少了,但是我稍后会讨论一点;最后他们用了一个朴素算法,在我们之后的BLOG还会学习到。
这些具体算法的细节不那么重要,这个实验就是选了四种分类算法,然后不断改变训练数据集的大小,尝试将这些学习算法用于不同大小的训练数据集中,看看训练集大小对不同算法的影响。下图就是他们得到的结果:
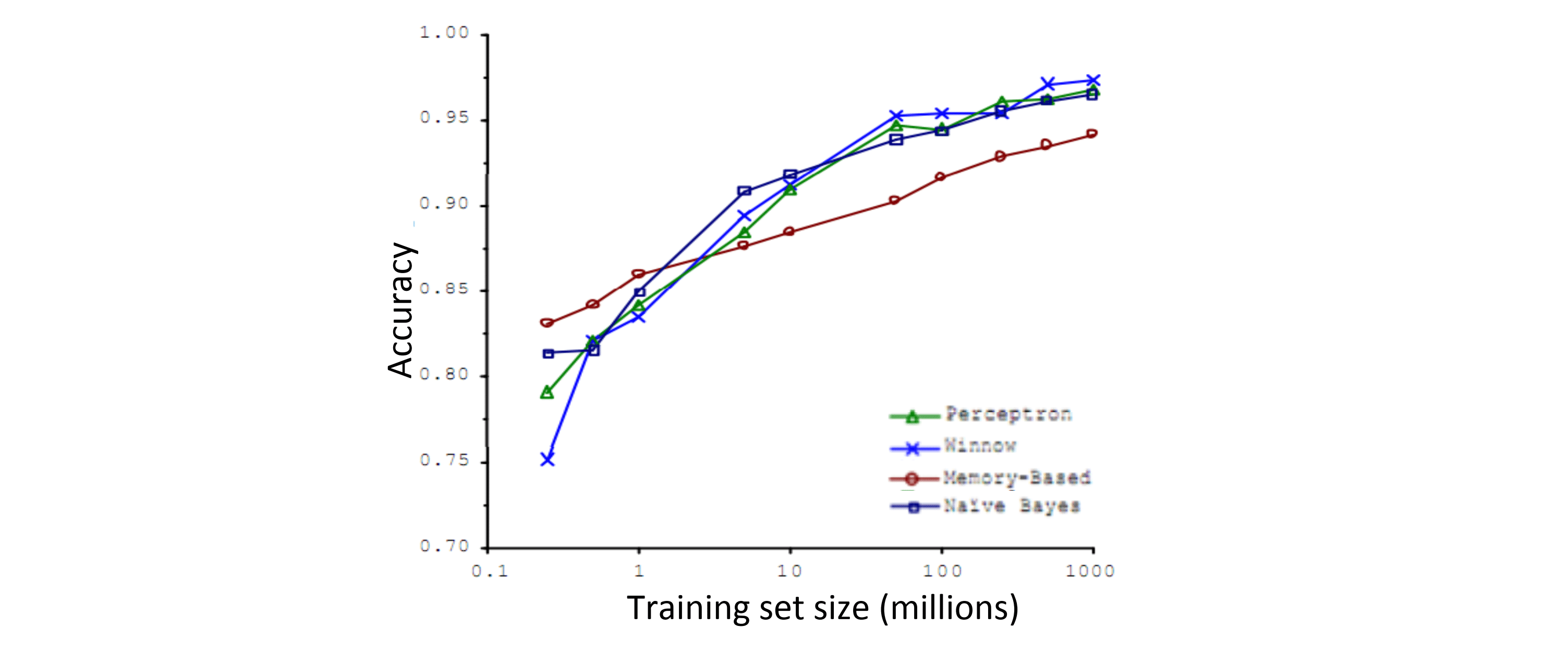
这些趋势非常明显。首先大部分算法都具有相似的性能,其次随着训练数据集的增大,在横轴上代表以百万为单位的训练集大小,从0.1个百万到1000百万,这些算法的性能也都对应地增强了。而且我们还发现一个有意思的事情,就是如果你选择任意一个算法,甚至可能选择了一个"劣等的"算法,但如果你给这个劣等算法更多的数据,那么从这些列子中看起来的话甚至有可能表现得会其他初期更优秀的算法更好。由于这项原始的研究非常具有影响力,因此到目前为止已经有一系列许多类似的研究,但都显示了相似的结果。这些结果都表明在训练数据足够多的情况下,许多不同的学习算法有时倾向于表现出非常相似的表现,当然取决于一些细节还是有一点点的差别,但是真正能提高性能的往往就是大量的训练数据。
这样的结果引起了一种在机器学习中的普遍共识: "取得成功的人不是拥有最好算法的人,而是拥有最多数据的人" 那么这种说法在什么时候是真什么时候是假呢?
数据=高性能算法?
因为如果我们有一个学习算法,并且如果以上的说法是真的,那么得到大量的数据通常就是保证我们具有一个高性能算法的最佳方式,而不是去争辩应该用什么样的算法该去怎么优化。
其实要满足数据=高性能算法这个等式,还需要几个条件。首先我们要有大量的有用的训练集且特征值 x ,其包含了足够的信息来帮助我们用来准确地预测 y 。比如说如果我们用上一部分的例子,我们要区分容易混淆的词,那么我们的特征向量 x 就要充分捕捉到需要填写的空白处周围的词语的特征,在特征捕捉到之后我们才希望有对于For breakfast I at __eggs(to,two,too)这个问题得到信息来告诉我中间我需要填的词是“两个” (two) 而不是单词 to 或 too 。因此特征捕捉一定要充分且能帮助我们推测 y ,哪怕是周围词语中的一个词都要能够给我一定的信息来确定出标签 y 是什么,特征值 x 需要有充足的信息来确定 y 。
举一个相反的例子,设想一个房子价格的问题,我们的数据集倘若只有房子大小信息,没有其他特征。那么如果我告诉你这个房子有 500平方英尺,但是我没有告诉你其他的特征信息,比如这个房子是否处在比较昂贵的区域,这所房子的房间数量,它里面陈设了多漂亮的家具,这个房子是新的还是旧的……这些信息我都不告诉你,只告诉你这个房子有500平方英尺,你能预测房子的售价吗?当然不行,因为除此除了房子的大小以外,还有许多其他因素会影响房子的价格。所以我经常思考对于一个问题,我需要哪些方面的参数。
为了解决这个问题,我们可以这样问自己:给定一个输入特征向量 x 的特征值范围,也给定了相同的可用的信息和学习算法;如果我们拿着这些数据去请教这个领域的人类专家,这个专家能够准确或自信地预测出 y 的值吗?
在第一个例子中,如果我们去找你认识的一个英语专家或者英语说得很好的人,他们可能不难预测出在这种情况下该使用什么样的词语。因此这就给了我信心,则为的单词作为特征向量的 x 能够让我们准确地预测 y 。但是与此相反如果我们去找一个价格上的专家,比如说是一个房地产经纪人或者职业售楼小姐,如果我只是告诉他们一个房子的大小,然后问他们房子的价格,那么即使是擅长房价评估的专家也很难告诉我房子的价格是多少。所以在房价的例子中,我们只知道房子的大小并不能带来足够的信息来预测。
也就是说在特征向量不够完备的情况下,再多的数据也可能成就不了一个完美的算法。
接着让我们来看一看大量的数据确定有帮助的情况。假设特征值有足够的信息来预测 y 值,即假设我们使用一种需要大量参数的学习算法,比如有很多特征的逻辑回归或线性回归或者带有许多隐藏单元的神经网络。这些参数可以拟合非常复杂的函数,所以通常都具有低偏差的特点,如果我们用一些数据运行这些算法,这种算法往往能很好地拟合训练集,但通常方差会比较大。
在这种情况下如果我们有一个庞大的训练集,那么尽管我们有很多参数,但是如果训练集比参数的数量级还大数倍,那么这些算法就不太可能会过度拟合,也就是说在这种情况下训练误差有希望接近测试误差。然后把这两个误差放在一起看看,训练集误差很小,而测试集误差又接近训练误差,这就意味着测试集的误差也会很小。
另一种考虑这个问题的角度是为了有一个高性能的学习算法,我们希望它不要有高的偏差和方,首先为了得到低的偏差,我么可以通过构造有一个具有很多参数的学习算法来保证;而为了得到低的方差,我们可以用非常大的训练集来保证。所以综合起来复杂的假设函数和大量的数据集可以铸就一个低误差和低方差的优秀学习算法,这就使得我们能够很好地测试数据集。
所以要让数据集发挥真正的作用,从根本上来说这是一个关键的要求:特征值有足够的信息量。如果我们有大量的数据,而且我们训练了一种带有很多参数的学习算法,那么我们得到的往往就是一个异常优秀的学习算法。
结语
通过这篇BLOG,相信你已经对训练数据的规模对学习算法的作用有了一定的想法, "取得成功的人不是拥有最好算法的人,而是拥有最多数据的人"是否正确也有了自己的答案。最后希望你喜欢这篇BLOG!