在上一篇BLOG中，我们提到了手动的误差分析和自动的数值误差分析也就是误差评估，但是仅仅靠简单的误差率来进行评估会出现不小的问题，这篇BLOG就让我们一探究竟。

查准率和召回率

在上一篇BLOG中，我们一同学习了误差分析以及设定误差度量值的重要性。有了算法的评估和误差度量值，有一件重要的事情要注意，就是使用一个合适的误差度量值，这有时会对于我们的学习算法造成非常微妙的影响。

如果我们只是用简单的样本误差率来作为误差度量值，那么我们在处理偏斜类（skewed classes）问题上就会出现问题。那什么是偏斜类问题呢？想一想之前的癌症分类的问题，我们拥有每位内科病人的特征变量，我们希望用我们的算法去判断他们是否患有癌症，就像要做恶性与良性肿瘤的分类问题一样。在这里我们假设 y = 1 表示患者患有癌症，假设 y = 0 表示他们没有得癌症。我们利用训练集训练出来了一个逻辑回归模型，然后用测试集检验了这个分类模， 并且发现它只有1%的错误即代表我们99%会做出正确诊断，看起来是非常不错的结果。但是我们发现在测试集中其实只有0.5%的患者真正得了癌症，因此在这个例子中 1% 的错误率就不再显得那么好了。

为什么呢？举个具体的例子下面有一行代码：

function y = predictCancer(x)
    y = 0;    %ignore x!
return

这显然不是机器学习代码，它直接忽略了输入值 X 让 y 总是等于 0 ，因此它总是预测没有人得癌症，但这个简陋的算法实际上只有 0.5% 的错误率，甚至比我们之前得到的 1% 的错误率更好。这种情况发生在正样本和负样本的数量比率非常接近于一个极端的时候，在这个例子中正样本的数量与负样本的数量相比非常非常少，所以就导致了问题的产生。我们把这种情况叫做偏斜类，其具体指的是一个类中的样本数与另一个类的数据相比多很多，我们通过总是预测y = 0 或者总是预测y = 1 算法可能表现非常好的问题。

因此在偏斜类下，使用分类误差或者分类精确度来作为评估度量可能会产生如下问题，假如说你有一个算法其精确度是99.2% ，只有0.8%的误差。但假设你对你的算法做出了一点改动现在你得到了 99.5% 的精确度，只有0.5%的误差。这到底是不是算法的一个提升呢？用某个实数来作为评估度量值的一个好处就是它可以帮助我们迅速决定我们是否需要对算法做出一些改进，比如将精确度从99.2%提高到99.5%从数据上看就是非常好的。但是我们的改进到底是有用的还是说 我们只是把代码替换成了总是预测 y = 0 这样的东西呢？所以在偏斜类下用简单的分类精确度并不能很好地衡量算法，因为你可能会获得一个很高的精确度非常低的错误率的算法，但是我们并不知道我们是否真的提升了分类模型的质量，因为显然总是预测 y = 0 并不是一个好的分类模型。所以当我们遇到一个偏斜类时，我们希望有一个不同的误差度量值或者不同的评估度量值。

其中一种比较主流的评估度量值是用查准率（precision）和召回率（recall）的评估。让我们一起来看一下，假设我们正在用测试集来评估一个分类模型，对于测试集中的样本都会等于 0 或者 1 ，我们的学习算法要做的是做出值的预测，预测值也是等于 0 或 1，下面是我画的一个基于实际的分类与预测的分类的 2x2 的表格：

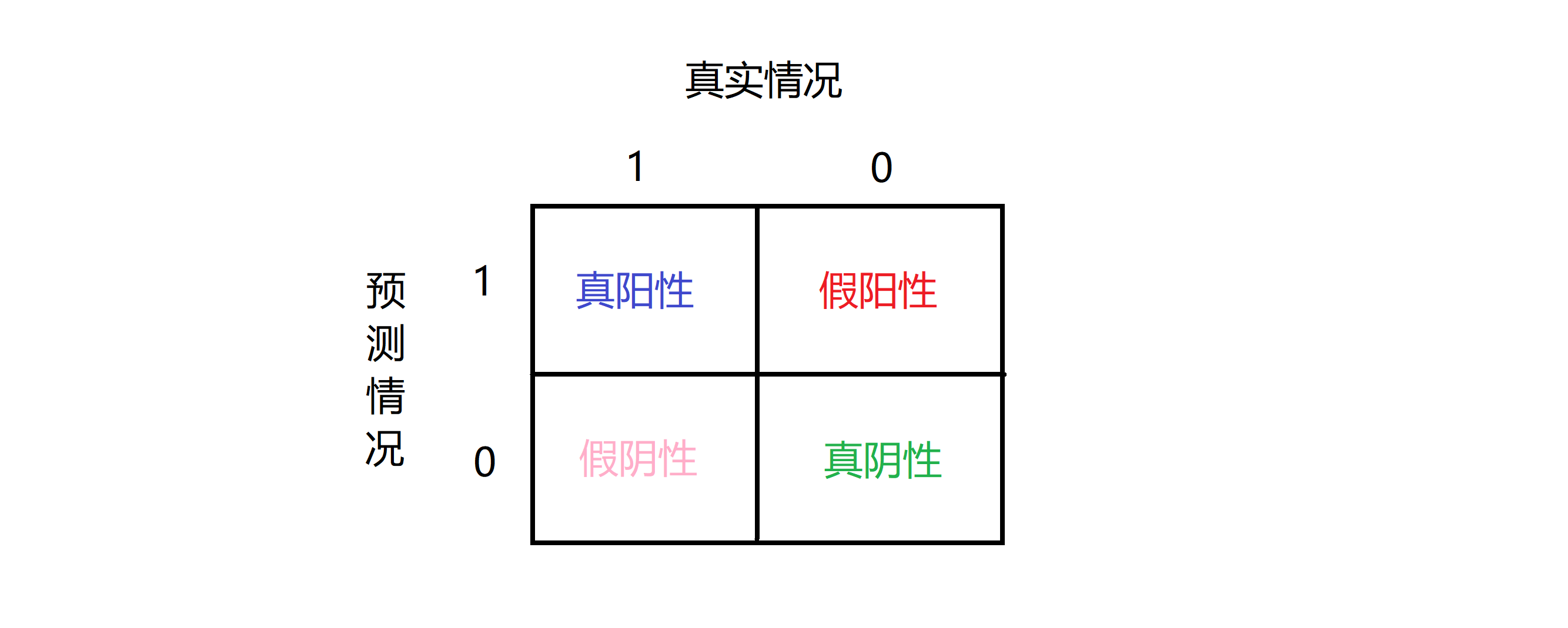
如果有一个样本它实际所属的类是 1 预测的类也是 1 那么我们把这个样本叫做真阳性（true positive）， 意思是说我们的学习算法预测这个值为阳性实际上这个样本也确实是阳性；如果我们的学习算法预测某个值是阴性等于 0 实际的类也确实属于 0 ，那么我们把这个叫做真阴性（true negative）。 还剩另外的两种情况，如果我们的学习算法 预测某个值等于 1 但是实际上它等于0，就叫做假阳性（false positive）； 如果我们的算法预测某个值等于 0 但是实际上它等于 1 ，就叫做假阴性（false negative）。

这样我们就有了一个基于实际类与预测类的2x2的表格，接下来我们就可以计算两个数字第一个叫做查准率，这个意思是对于我们的预测的所有患有癌症的病人，有多大比率的病人是真正患有癌症的，其计算公式显然如下：

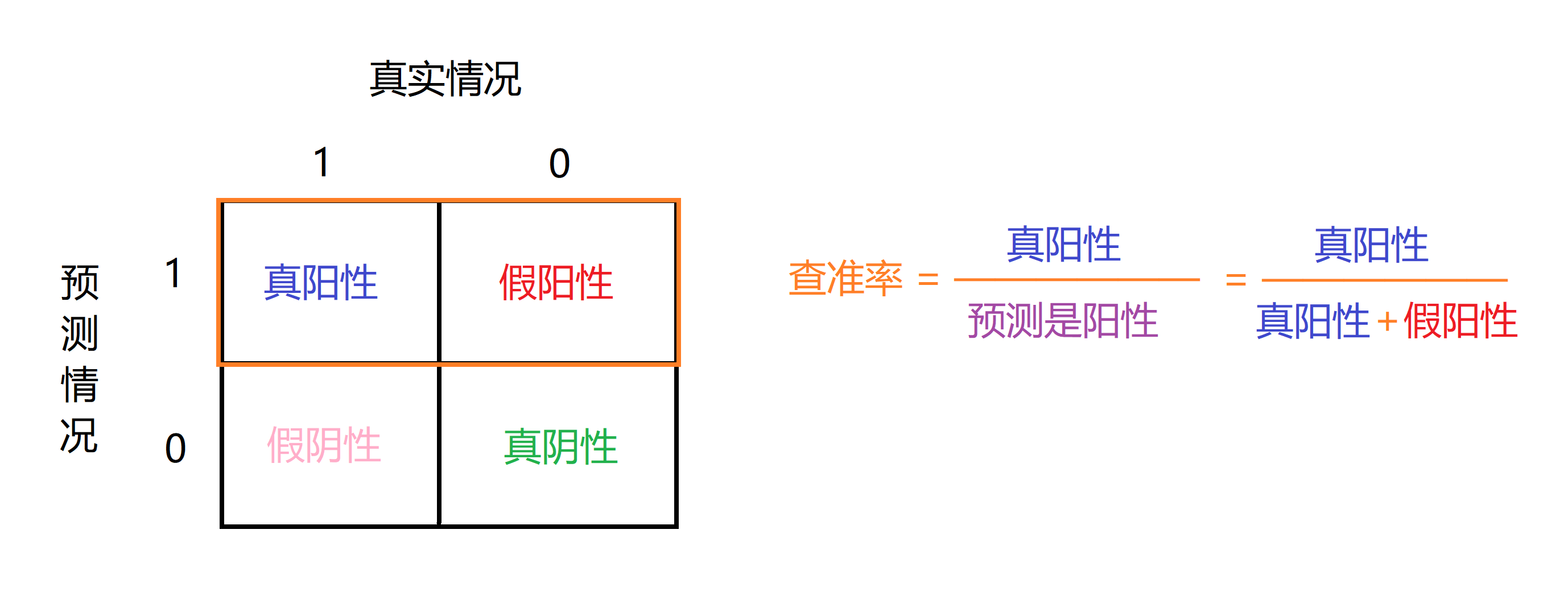
查准率越高就越好，高查准率说明我们对预测得了癌症的病人有很高的准确率。

另一个数字我们要计算的叫做召回率，召回率是指真正得了癌症的病人，有多大比率我们正确预测他们得了癌症。同样地，计算公式显然如下：

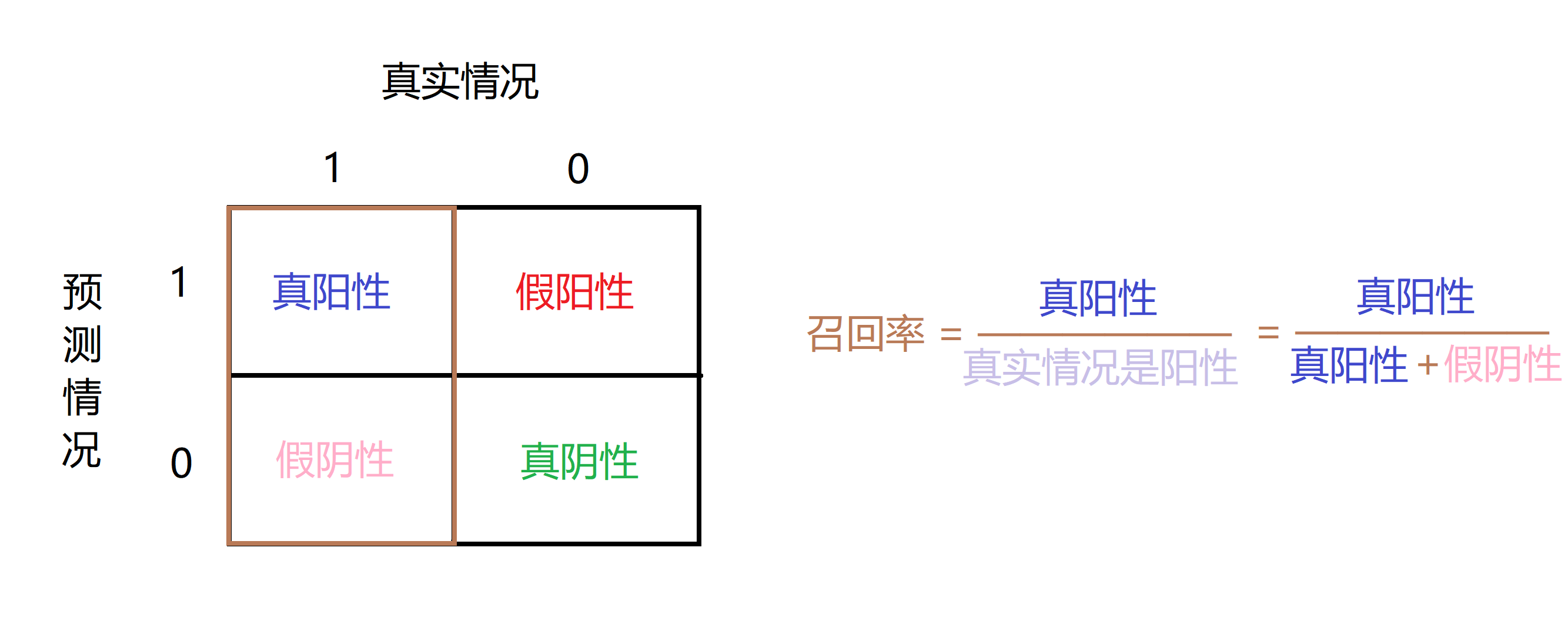
同样地，召回率越高越好。

通过计算查准率和召回率我们能更好的知道分类模型到底好不好。具体地说如果我们有一个算法，它总是预测 y = 0 它总是预测没有人患癌症，那么这个分类模型召回率就等于 0 ，因此我们能会快发现这个分类模型总是预测y = 0并不是一个好的模型。总的来说即使我们有一个非常偏斜的类，通过计算查准率和召回率，我们的算法也不能够 "欺骗"我们。仅仅通过预测 y 总是等于 0 或者 y 总是等于 1 ，它没有办法得到高的查准率和高的召回率。因此我们能够更肯定拥有高查准率或者高召回率的模型是一个好的分类模型。这就给予了我们一个更好的评估值和一种更直接的方法来评估模型的好与坏。最后一件需要记住的事，在查准率和召回率的定义中，我们总是习惯性地用 y =1 代表那个出现得非常少的类比如癌症。

总的来说，对于偏斜类的问题查准率和召回率给予了我们更好的方法来检测学习算法表现如何，这是一种更好地评估学习算法的标准，当出现偏斜类时其效果往往比仅仅只用分类误差或者分类精度好。

相对平衡的保持

在上一篇BLOG中，我们谈到查准率和召回率作为遇到偏斜类问题的评估度量值的好处。在很多应用中我们希望能够保证 查准率和召回率的相对平衡，所以这一部分我们就来看看具体应该怎么做同时也一同学习查准率和召回率作为算法评估度量值的更有效的方式。

下图是查准率和召回率的定义：

让我们继续用癌症分类的例子，如果病人患癌症则y = 1，反之则y = 0。假设我们用逻辑回归模型训练了数据输出概率在 0 - 1 之间的值，因此我们预测 y = 1 如果 h(x) 大于或等于0.5，预测值为 0 如果方程输出值小于 0.5。

但是现在假如我们希望在非常确信地情况下才预测一个病人得了癌症，因为你知道如果你告诉一个病人告诉他们得了癌症，他们会非常震并且经历一段非常痛苦的治疗过程，所以我们希望只有在我们非常确信的情况下才告诉这个人他得了癌症。达到这个目的的一种方法是修改算法，我们不再将临界值设为0.5 ，我们可以在 h(x)的值大于或等于 0.7 的情况下才预测 y = 1 ，这代表我们会告诉一个人他得了癌症只在我们认为他有大于等于 70% 得癌症的概率情况下。如果我们这么做那么我们的回归模型会有较高的查准率，因为所有我们准备告诉他们患有癌症的病人都有比较高的可能性真的患有癌症；但与之相反这个回归模型会有较低的召回率，因为当我们做预测的时候我们只给很小一部分的病人预测 y = 1，所以很多人可能会错失治疗的最佳时机。因此这是一个高查准率的模型但是召回率会很低的算法。

现在我们考虑一个不同的例子，假设我们希望避免遗漏掉患有癌症的人，因为如果一个病人实际患有癌症但是我们并没有告诉他患有癌症，那这可能造成严重后果。这种情况下，我们希望较为激进地预测 y = 1 ，这样他们会做进一步的检测然后接受治疗，以避免他们真的患有癌症。所以在这种情况下我们可以将临界值设得较低，比如0.3。这样做只要认为病人有大于 30% 的几率患有癌症，我们就会以更加保守的方式告诉他们可能患有癌症，请求他们能够接受治疗。在这种情况下我们会有一个较高召回率的模型，因为确实患有癌症的病人有很大一部分被我们正确标记出来了；但是我们会得到较低的查准率，因为我们预测患有癌症的病人比例越大，那么就有较大比例的人其实没有患癌症。

有的同学可能会问，为什么一定要从两面来看这个问题呢？为什么我们总是只想要高查准率或高召回率，这看起来可以使两边都提高。其实这是因为更普遍的一个原则是哪个高取决于我们想要什么，是想要高查准率低召回率还是高召回率低查准率。对于大多数的回归模型我们得权衡查准率和召回率，因为他们两个一般是呈现反比的形式：

查准率-召回率曲线可以是各种不同的形状，有时它看起来是这样有时是那样，这取决于回归模型的具体算法：

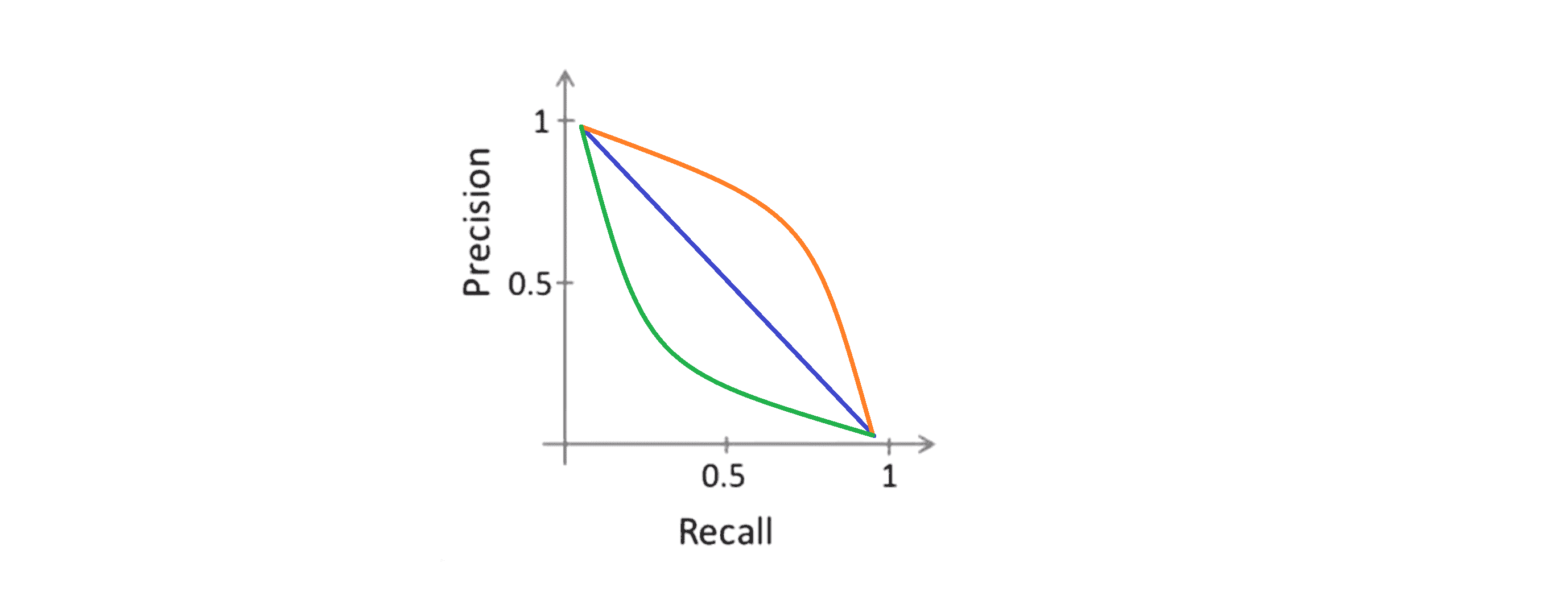
因此这又产生了另一个有趣的问题，那就是有没有办法自动选取临界值或者更广泛地说如果我们有不同的算法或者不同的想法，我们如何比较不同的查准率和召回率之间的优劣呢呢？

举个例子，假设我们有三个不同的学习算法，其临界值不同，我们怎样决定哪一个算法是最好的：

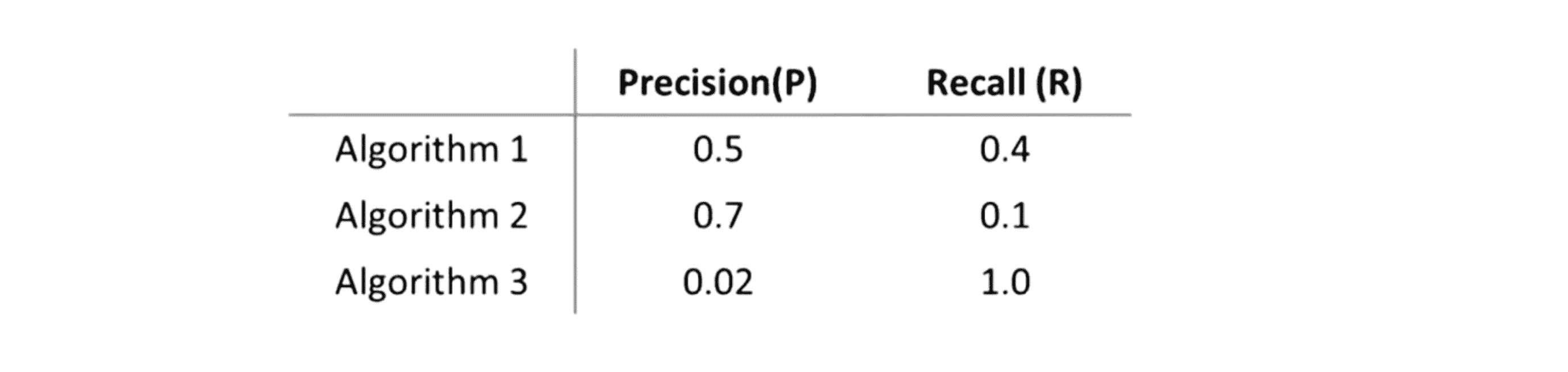
如果我们正在试图比较算法 1 和算法 2 ，我们就会问自己 到底是 0.5 的查准率与 0.4 的召回率好还是说 0.7 的查准率与 0.1 的召回率好。但如果每一次我们设计一个新算法都要坐下来思考到底0.5 0.4好还是说 0.7 0.1好，这就会大大降低我们的决策速度。所以如果我们有一个评估度量值能够告诉我们到底是算法 1 好还是算法 2 好就能够帮助我们更快地决定到底哪一个算法更好，同时也能够更快地帮助我们评估不同的改动，评估哪些应该被融入进算法里面。

那么我们怎样才能计算出这个评估度量值呢？我们可能会去尝试的一件事情是去计算查准率和召回率的平均值，但是这可能并不是一个很好的解决办法：

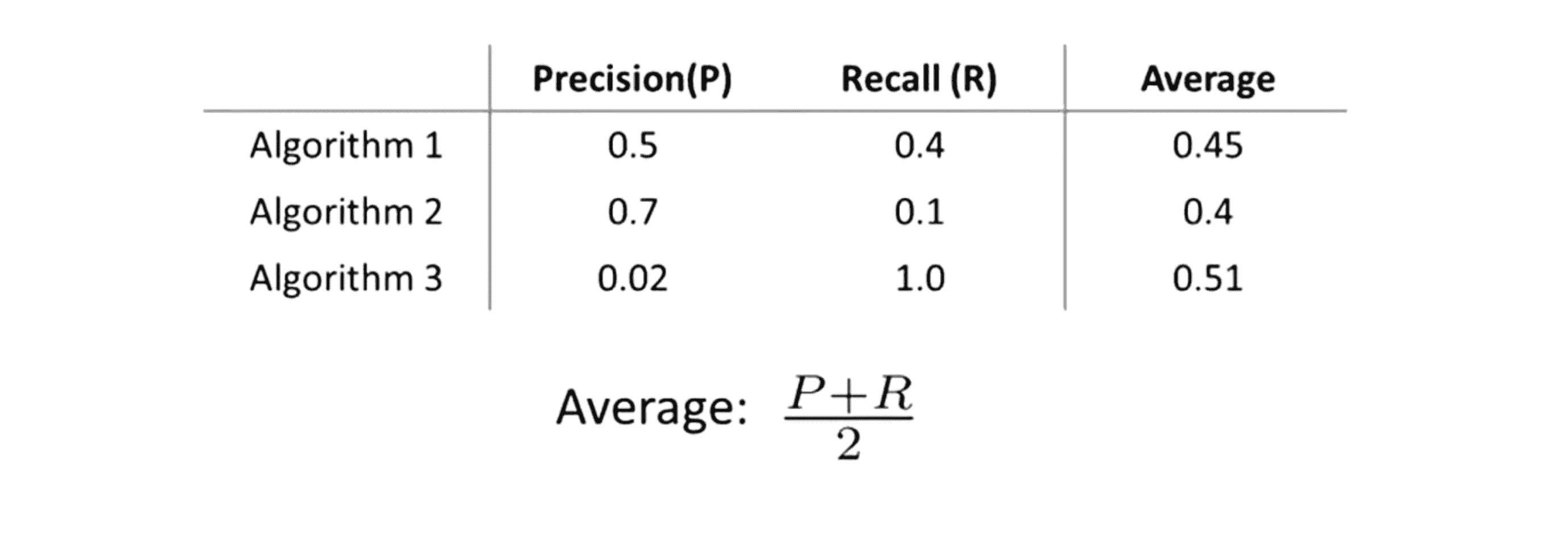
因为如果我们的回归模型总是预测 y = 1 这么做你可能得到非常高的召回率得到非常低的查准率，相反地如果我们的模型总是预测 y = 0 最后就会得到非常高的查准率和非常低的召回率，这两个极端情况的平均值都很大，但显然这并不是一个好的模型。此我们通常认为查准率和召回率的平均值不是评估算法的一个好的方法。

相反地我们有一种结合查准率和召回率的不同方式叫做F值，公式是这样：

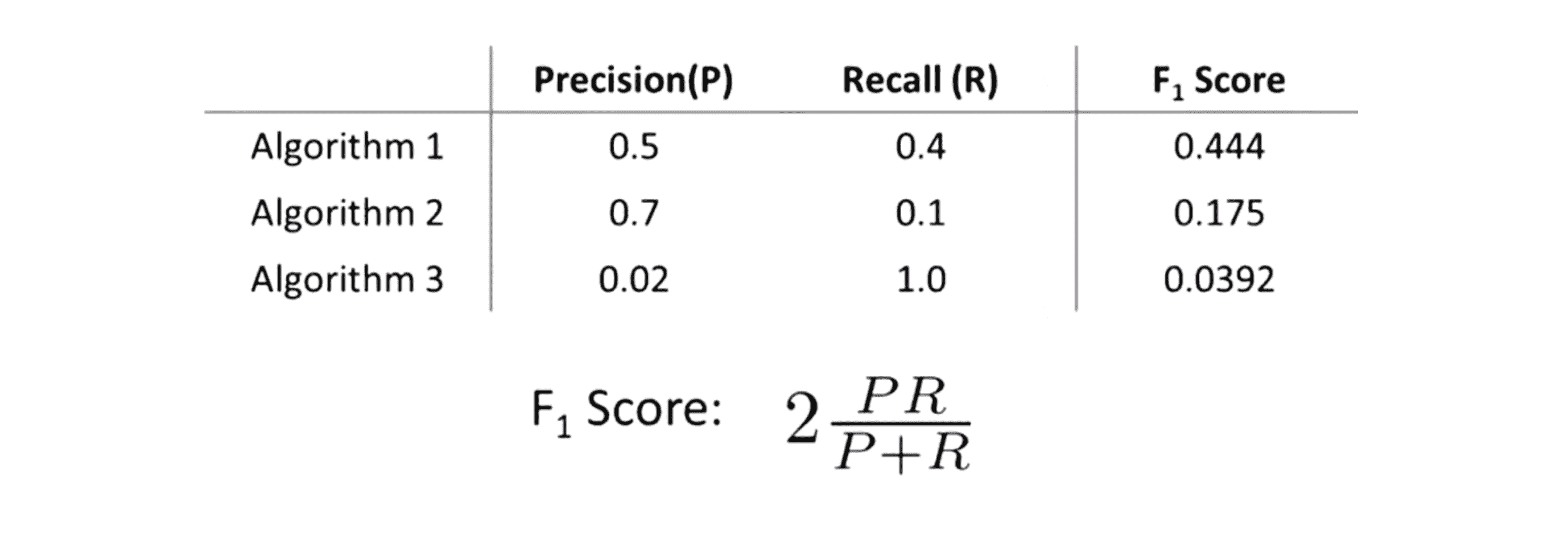
在这个例子中算法 1 有最高的F值，算法 2 第二，算法 3 是最低的。因此通过F值我们会在这几个算法中选择算法 1。 F 值也叫做 F1 值，一般写作F1值但是人们一般只说F值，它的定义会考虑一部分查准率和召回率的平均值，但是它会给查准率和召回率中较低的值更高的权重，因此可以看到F值的分子是查准率和召回率的乘积，因此如果查准率等于 0 或者召回率等于0，F值也会等于0。其实有较多的公式可以结合查准率和召回率， F 值公式只是其中一个，但是出于历史原因和习惯问题，人们习惯在机器学习中使用 F 值。而如果要得到一个很高的F值，我们的算法的查准率和召回率都要接近于 1，具体地说如果查准率=0或者召回率=0，我们的F值也会等于0；而对于一个最完美的F值，如果查准率等于1，同时召回率也等于1，那我们得到的F值就会等于 1 。

所以在变动临界值后，我们可以通过 F 值的计算来控制权衡查准率和召回率，来帮助我们自动选择临界值，以大大增加效率。

结语

通过这篇BLOG，相信你已经会解决不对称分类的误差评估问题并且可以熟练使用F值了。最后希望你喜欢这篇BLOG！