在之前的BLOG里，我们一同学习了线性回归，逻辑回归，神经网络等诸多算法。而在这篇BLOG，我们就要一同学习一种更加强大的算法——支持向量机(Support Vector Machine)，以带给我们一个更加方便快捷的监督学习解决方法。

优化目标

支持向量机(Support Vector Machine)或者简称SVM，是一种在学习复杂的非线性方程时更为清晰更加强大的学习算法，正如我们之前学习算法的步骤一样，让我们先从这个算法的优化目标开始。让我们先从之前学习过的逻辑回归开始，看看我们如何一点一点修改得到支持向量机。让我们先回顾一下逻辑回归，下图是逻辑回归的代价函数和S型激励函数：

一样地，我们用 z 来表示 θ^T * x 。现在让我们通过这个代价函数，一起来考虑下逻辑回归在处理样本时会做什么。

假如我们有一个 y = 1 的样本，我们就希望此时 h(x) 趋近 1 ，因为我们想要正确地将此样本分类，这就意味着当 h(x) 趋近于1时，z = θ^T * x >> 0。通过上图的 S 型函数我们可以看到我们的 z 越大，我们的这个样本产生的代价 y 就越小：

相反地，如果我们有另一个样本y = 0，那我们就会希望此时假设函数的输出值趋近于 0，即 z = θ^T * x << 0 。通过上图的 S 型函数我们可以看到我们的 z 越小，我们的这个样本产生的代价 y 就越小。

一个训练样本所对应的偏差值可以用下面这个公式计算：

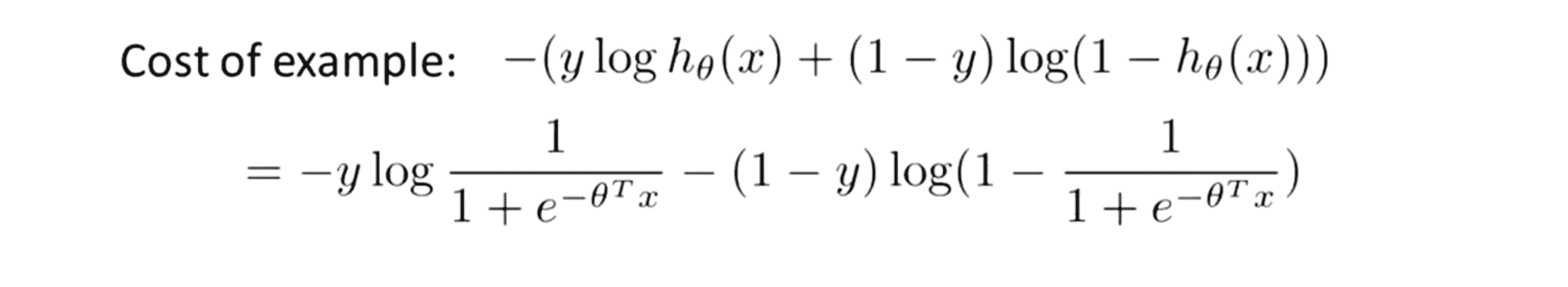
而总的代价函数就是所有的训练样本产生的代价求和再求平均值：

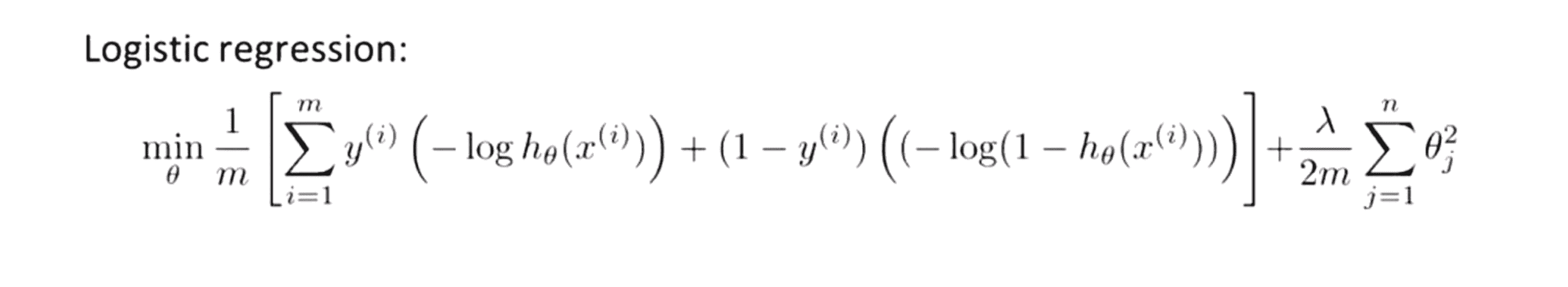
现在一起来考虑两种分开的情况，一种是y = 1的情况，一种是y = 0的情况。在第一种情况中，假设 y = 1 ，此时在目标函数中只有第一项起作用，因为y = 1时 (1 - y) = 0，因此，当在y = 1的样本中时，我们得到的代价是 -log(1/(1+e^z) ) 。同样地，我们用 z 表示 θ^T * x。如果这时画出代价关于 z 的函数，我们就会会看到下图的这条曲线：

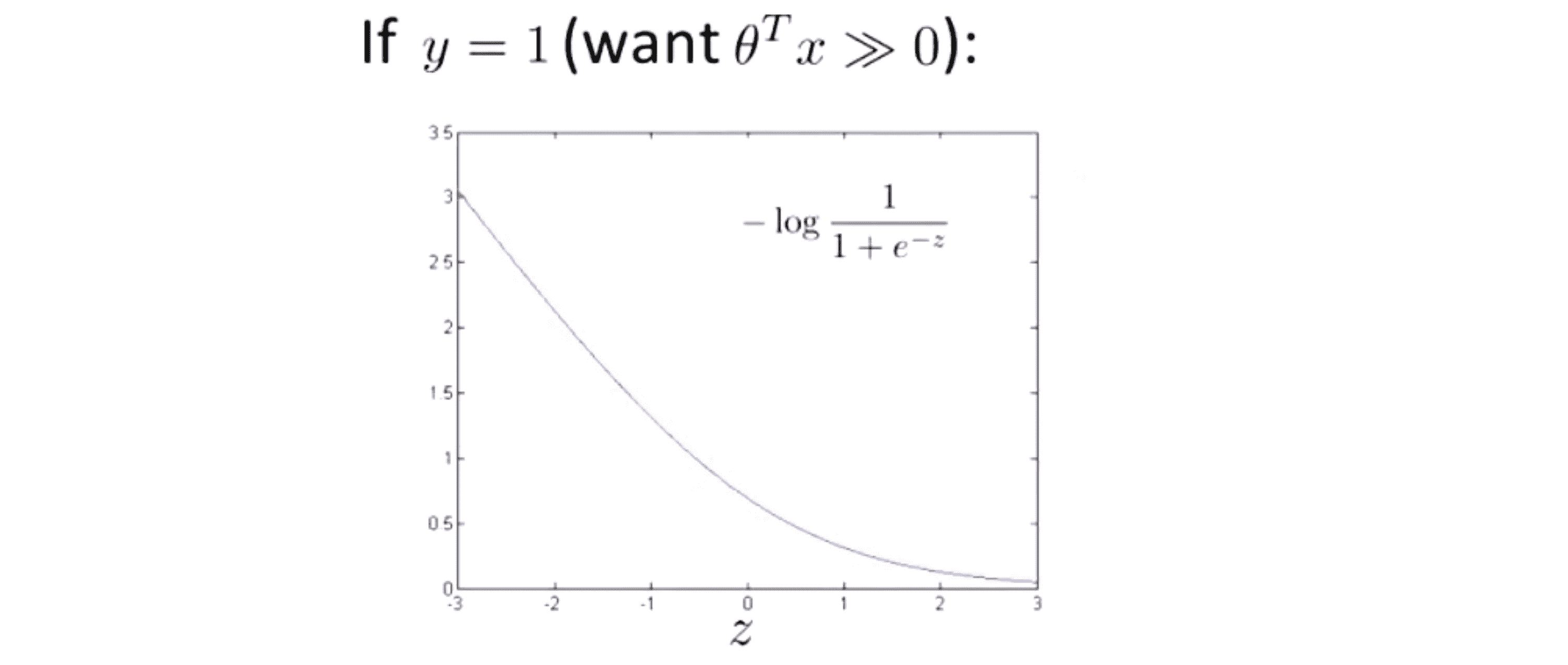
我们同样可以看到，当 z 增大时对应的代价值会变的非常小，对整个代价函数而言影响也非常小。这也就解释了为什么逻辑回归在观察到正样本 y = 1 时，会试图将 θ^T * x设置的非常大。现在，我们开始建立支持向量机我们来修改一下代价函数图像也就是 -log(1/(1+e^z))：

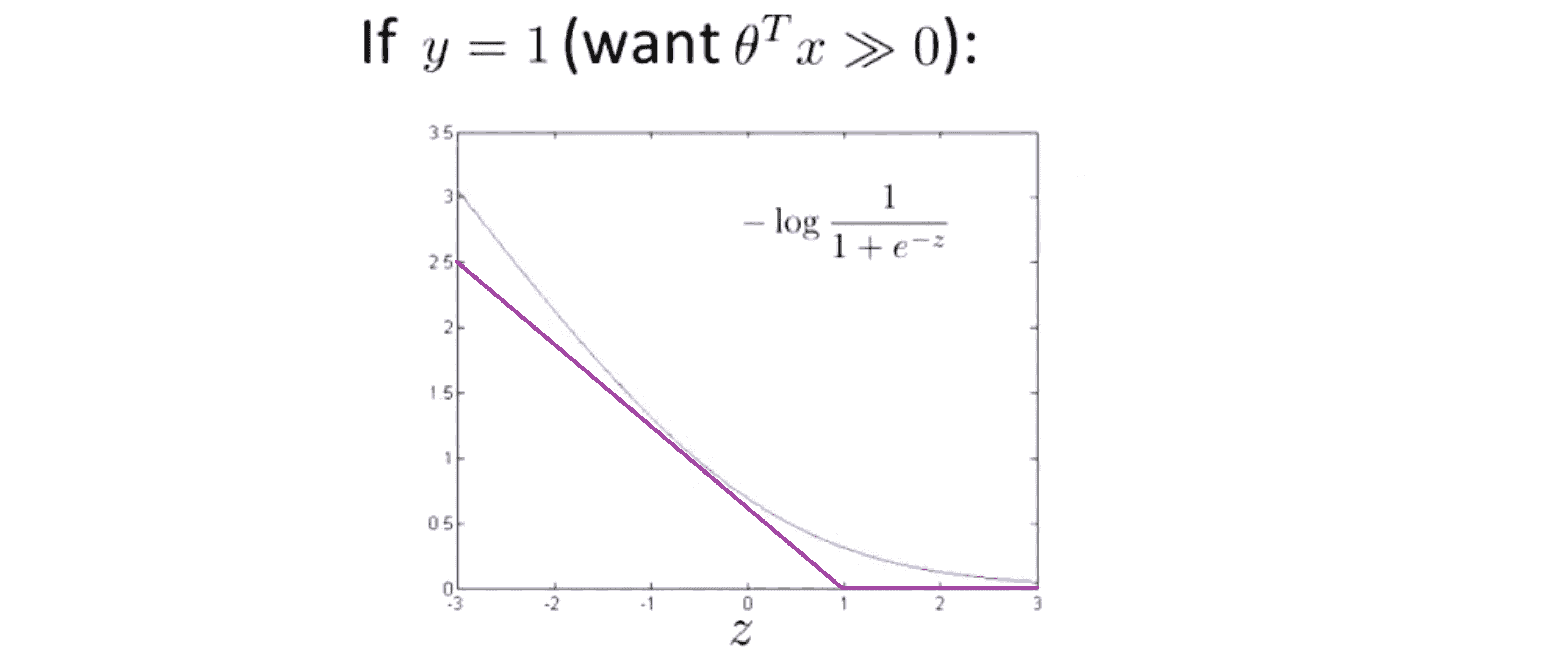
首先在 z ≥ 1 时，新的代价函数将会水平向右延伸，然后我再画一条同逻辑回归非常相似的直线去拟合z < 1的情况。其实这已经非常接近逻辑回归中使用的代价函数了，只是这里是由两条线段组成，即包括位于右边的水平部分和位于左边的直线部分。先别过多的考虑左边直线部分的斜率，这并不是很重要，这里我们将使用的新的代价函数，这会在之后的的优化问题中，变得更便捷， 带来计算上的优势。

我们只是讨论了 y = 1 的情况，另外一种情况是当 y = 0 时，此时 如果我们仔细观察代价函数，就发现第一项会因为 y = 0而全部等于 0 ，只留下了第二项。并且如果我们将这一项作为 z 的函数，那么我们就得到了下面这个图像：

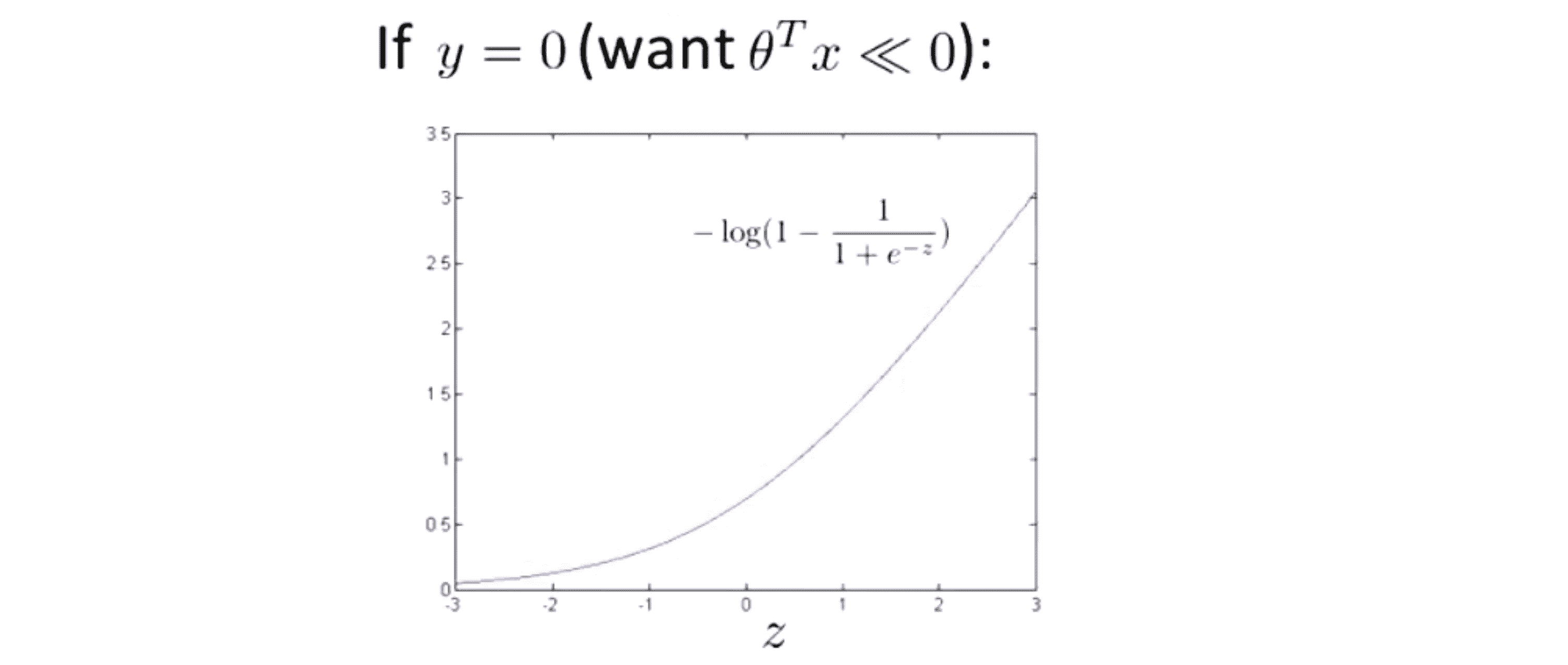
同样地我们用相似的方法来产生一个新的代价函数来代替旧的图像。首先 z ≤ -1 还是一条贴着坐标轴的水平直线，然后是一条斜线：

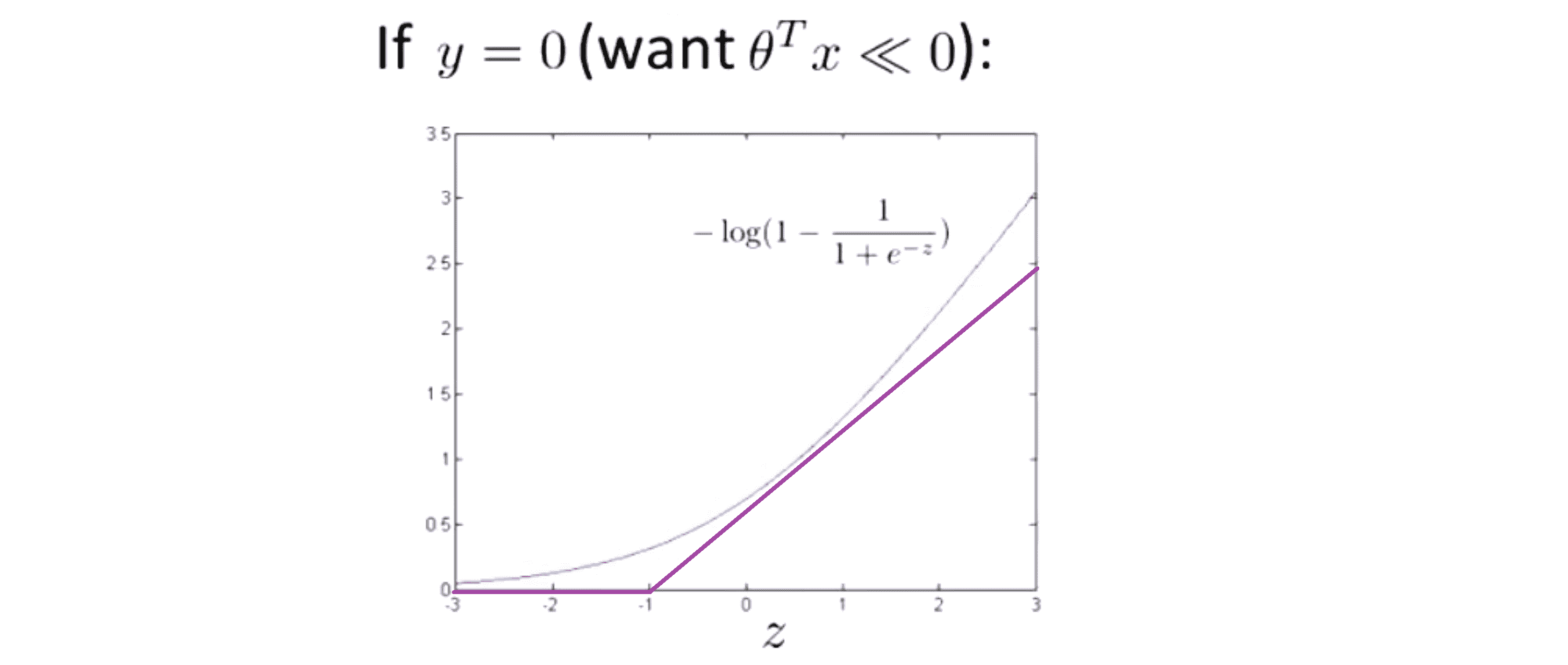
现在现在让我给这两个新的方程命名，之前 y = 1 的情况的新函数，我称之为 cost1(z)，同时 y = 2 的情况的性函数我称之为 cost0(z)。拥有了这些定义后，我们就可以正式开始构建支持向量机。

下图时我们之前在逻辑回归中使用的代价函数 J(θ)：

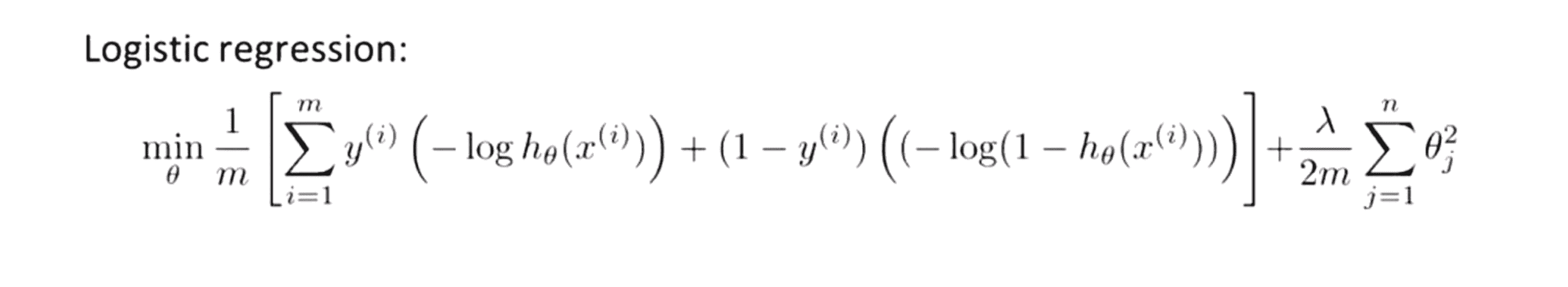
对于支持向量机而言，实质上我们要将这前一个函数项替换为 cost1(z) 也就是cost1(θ^Tx)，同样地我们也将后一个函数项替换为cost0(z)，也就是代价 cost0(θ^Tx)：

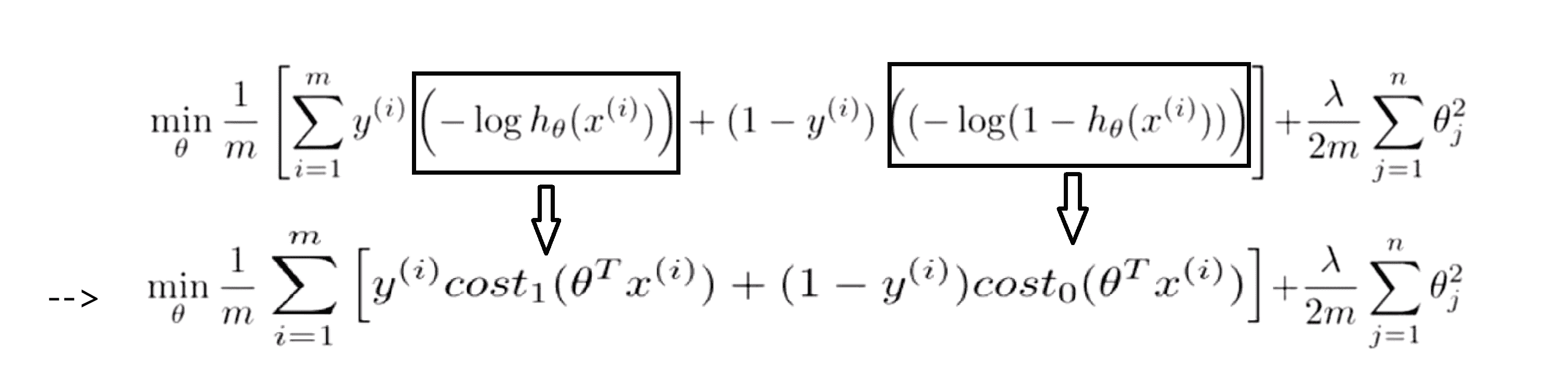
我们就得到了支持向量机的大致代价函数。事实上在实际情况下我们的书写会稍微有些不同，代价函数的参数表示也会稍微有些不同。按照人们的约定，首先我们要除去 1/m 这一项，当然这仅仅是由于人们使用支持向量机时对比于逻辑回归而言不同的习惯所致。由于 m 只是一个常数，所以仅仅除去 1/m 这一项还是可以得出同样的 θ 最优值：

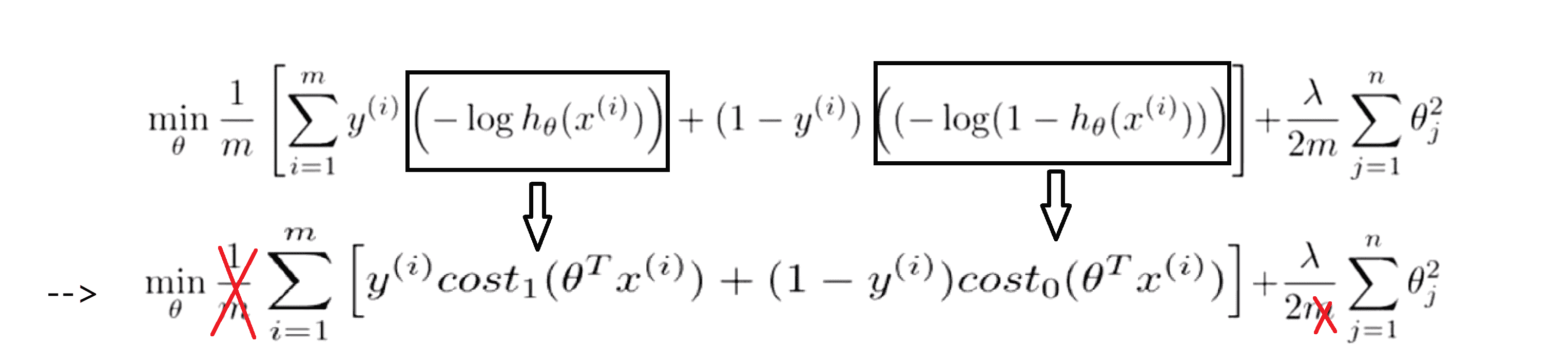
接着对于逻辑回归，在目标函数中我们有个正则化参数 λ，我们把前一大项设为 A ，λ 后的设为 B ，那我们就有J = A + λ * B。然后通过设置不同正则参数 λ 就能达到不一样的正则化优化目的。但对于支持向量机，按照惯例我们将使用一个不同的参数来替换这里使用的 λ 来权衡这两项 你知道。若我们引入一个一个新的参数称为 C ，则J = C * A + B 其实很显然和我们之前的J = A + λ * B的效果是等价的。C 和 λ 一样都是为了权衡 A 和 B 所占比重的。当然你也可以把这里的参数C考虑成 1/λ ，因为其同 1/λ 所扮演的角色相同。

通过这些改变我们就得到了支持向量机中的整个优化目标函数：

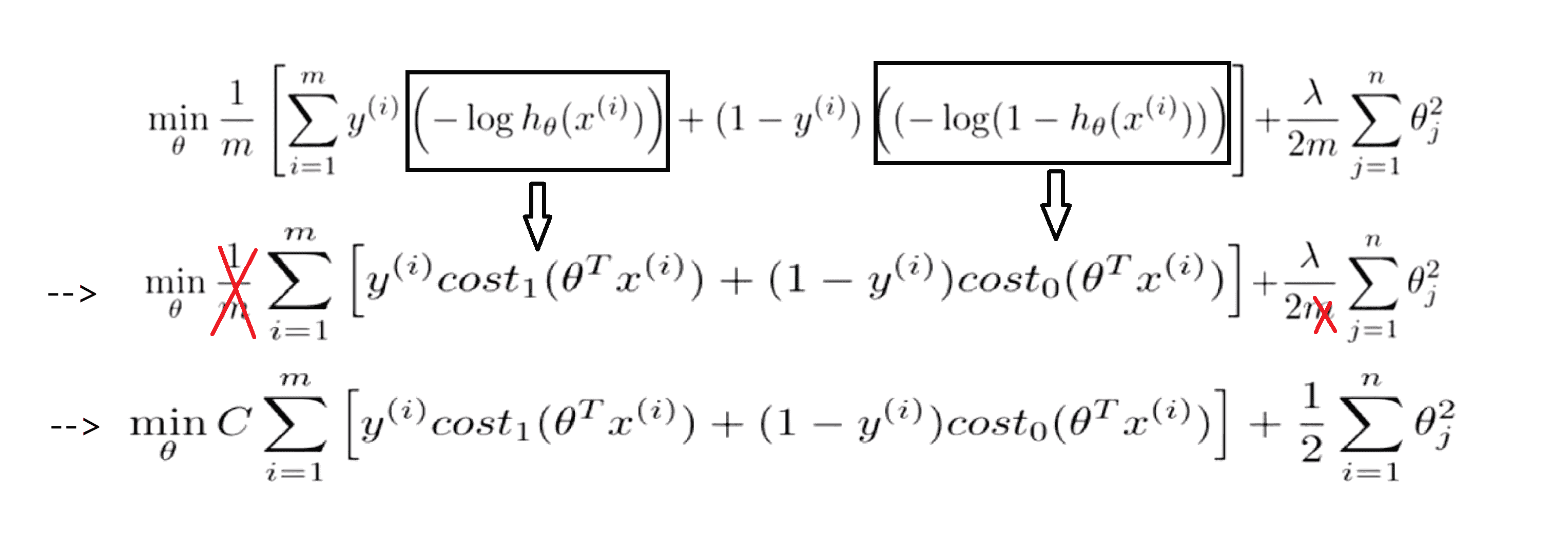
通过最小化这个目标函数，我们就能得到最优的θ。最后有别于逻辑回归的一点，逻辑回归输出的是概率，但是支持向量机器（SVM）是来直接预测 y 的值等于 1 还是等于 0。

以上就是支持向量机在数学上的定义，在接下来的部分我们会从直观的角度看看优化目标实际上是在做什么。

大间隔分类器

人们有时将支持向量机说做是大间距分类器，在这一部分我们将一同学习其中的含义，这有助于我们直观理解 SVM 模型的假设具体是什么样的。下图是我们的支持向量机模型的代价函数：

现在让我们考虑一下最小化这些代价函数的必要条件是什么。假如我们有一个正样本，即y = 1，则只有在 z = θ^T x ≥ 1时，代价函数 cost1(z) 才等于 0。换句话说，如果我们有一个正样本，我们会希望 θ^T x ≥ 1。反之如果是一个负样本，即 y = 0，我们发现它只有在 z ≤ 1 的区间里函数值才是为 0，所以这时我们会希望我们的θ^T x ≤ 1 。这是支持向量机的一个有趣性质，因为在逻辑回归中，如果你有一个正样本 y = 1，则其实我们仅仅要求 θ^T x ≥ 0 就能将该样本恰当分出； 类似地逻辑回归中，如果我们有一个负样本，则仅需要θ^T * x ≤ 0 就会将负例正确分离。但是支持向量机的要求更高，它不仅仅要能正确分开输入的样本，还嵌入了一个额外的安全因子或者说安全的间距因子。当然逻辑回归也做了类似的事情，但是让我们看一下在支持向量机中这个因子会导致什么结果。

具体而言，我们接下来会考虑一个特例，我们将这个常数 C 设置成一个非常大的值，然后来观察支持向量机会给出什么结果。如果 C 非常大，则最小化代价函数的时候我们将会很希望找到一个使第一项为 0 的最优解。

举个例子，如果你考虑下图这样一个数据集，其中有正样本也有负样本：

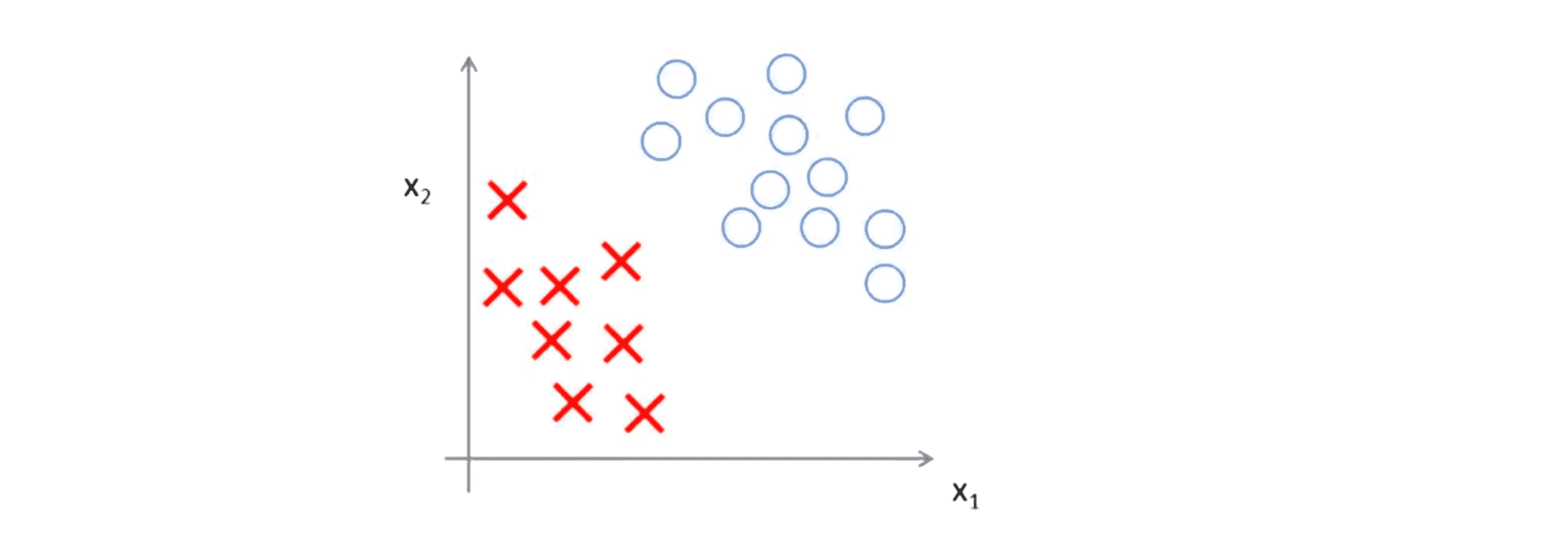
可以看到这个数据集是线性可分的，即存在一条直线把正负样本分开，比如下图中绿线就是一个决策边界，可以把正样本和负样本分开，但是多多少少这个看起来有点不自然：

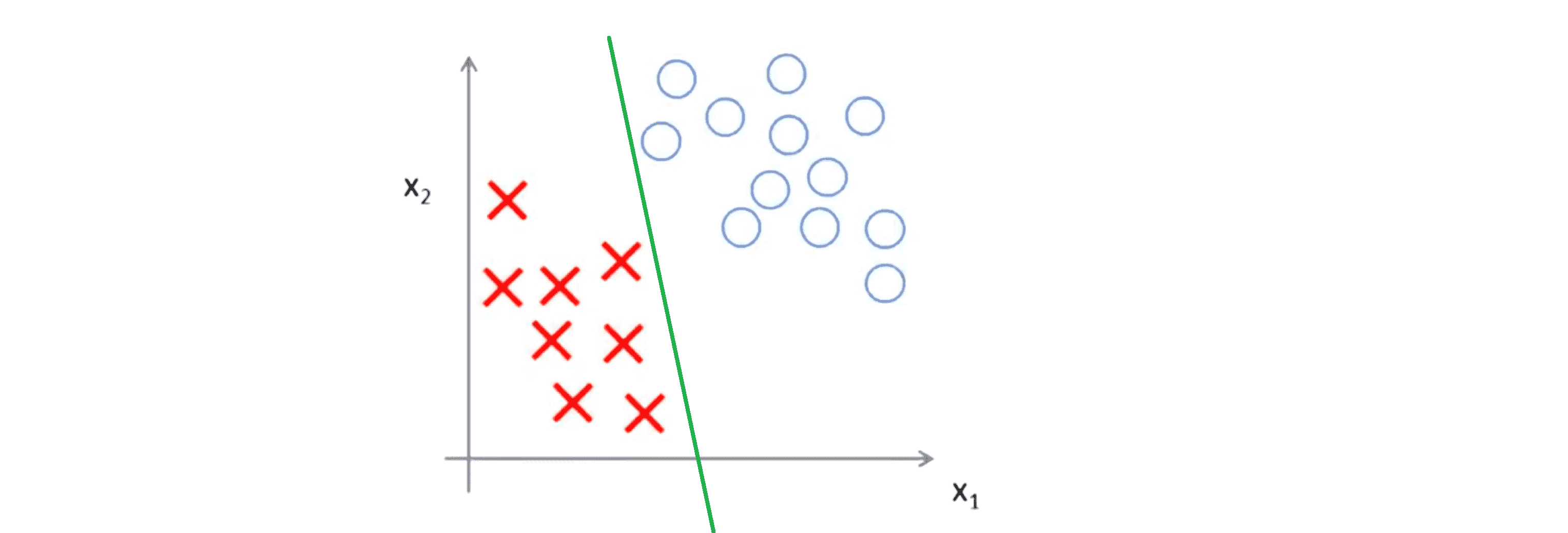
我们甚至可以画一条更不自然的决策界，但仅仅是勉强分开，如下图中红线：

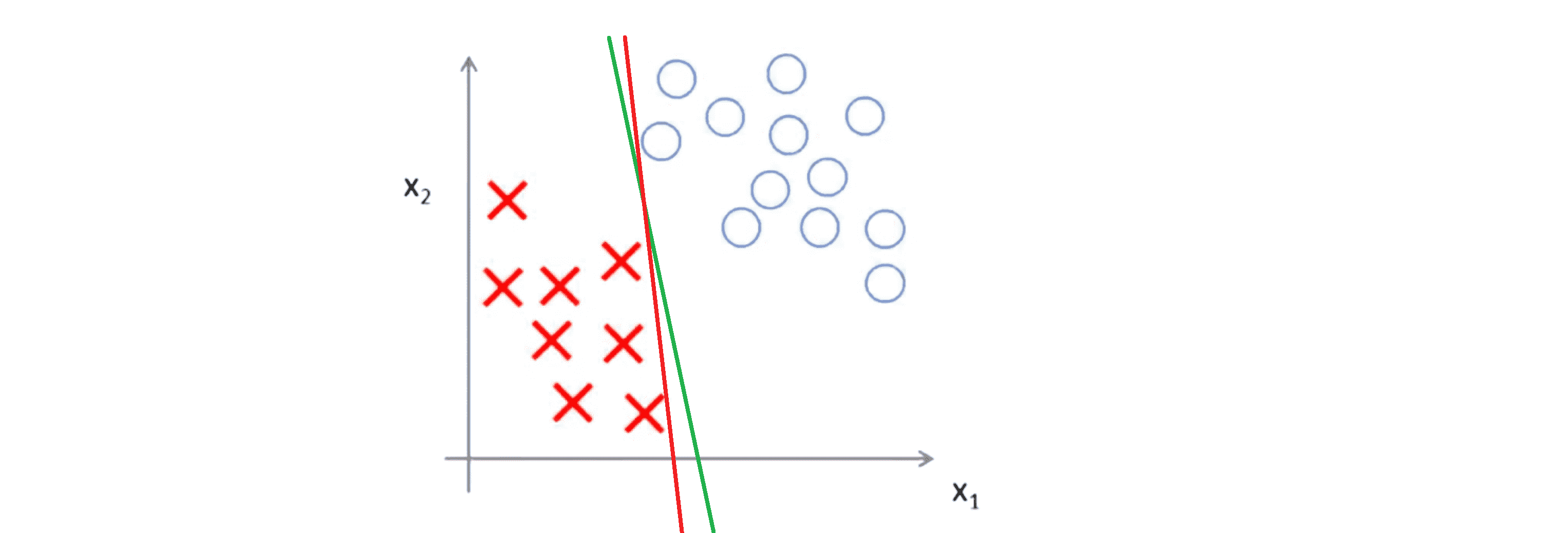
这些决策边界看起来都不是特别好的选择。而支持向量机将会选择下图这个黑色的决策边界：

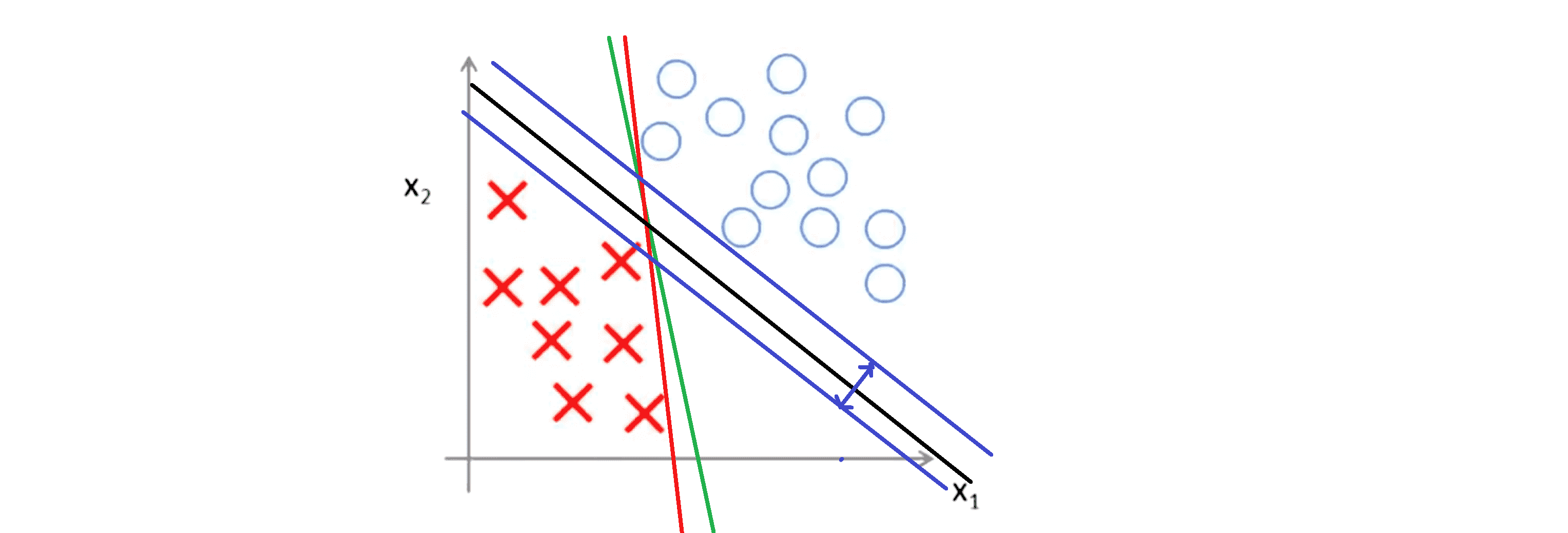
相较于之前我用红色或者绿色画的决策界，这条黑色的看起来好得多，黑线看起来是更稳健的决策界。从数学上来讲，这条黑线有更大的距离，这个距离叫做间距 (margin) 。当画出这两条额外的蓝线，我们看到黑色的决策界和训练样本之间有更大的最短距离，然而红线和绿线就离训练样本就非常近，所以它们在分离样本的时候就会比黑线表现差。这个距离就叫做支持向量机的间距，而这是支持向量机具有优越性的原因。因为它努力用一个最大间距来分离样本，因此支持向量机有时被称为大间距分类器。

你也许好奇我们新的代价函数的优化问题为什么会产生这个结果，它是如何产生这个大间距分类器的呢？

不要着急，在下一部分，我就用数学的方式展示给你看。这一部分关于大间距分类器，我想讲最后一点，在之前的例子中，我们将这个大间距分类器中的正则化因子也就是常数 C 设置的非常大，因此对下图这样的一个数据集：

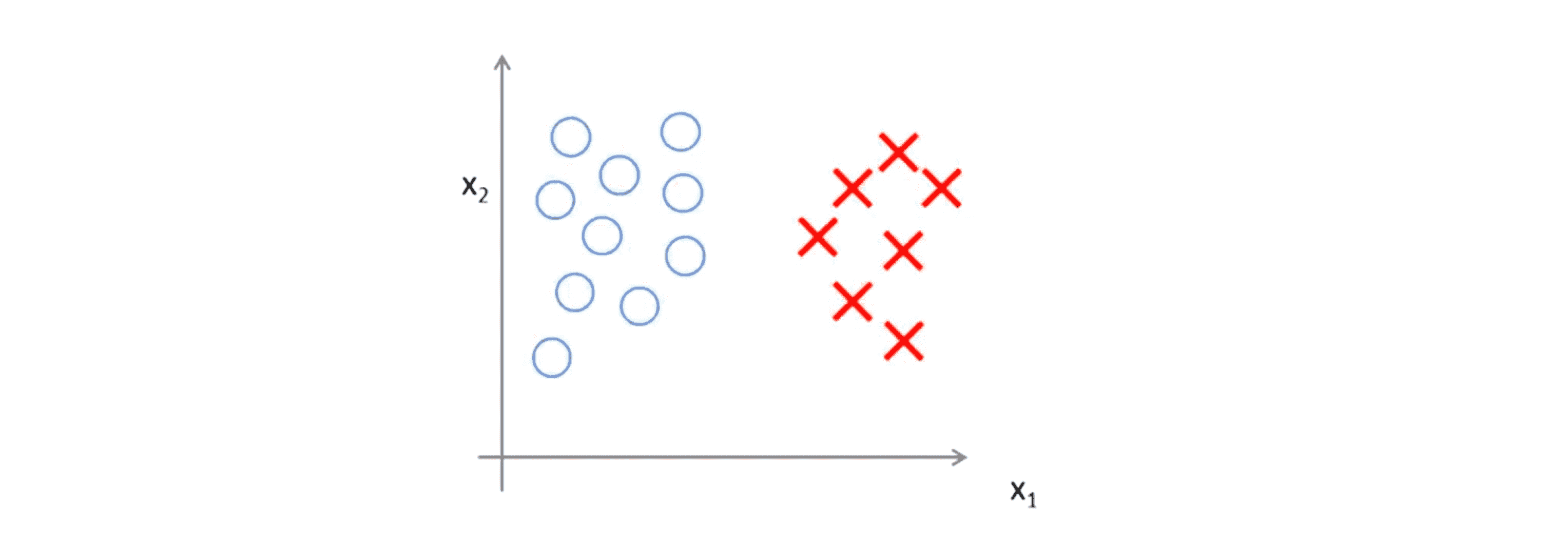
也许我们将选择下图这样的决策界从而最大间距地分离开正样本和负样本：

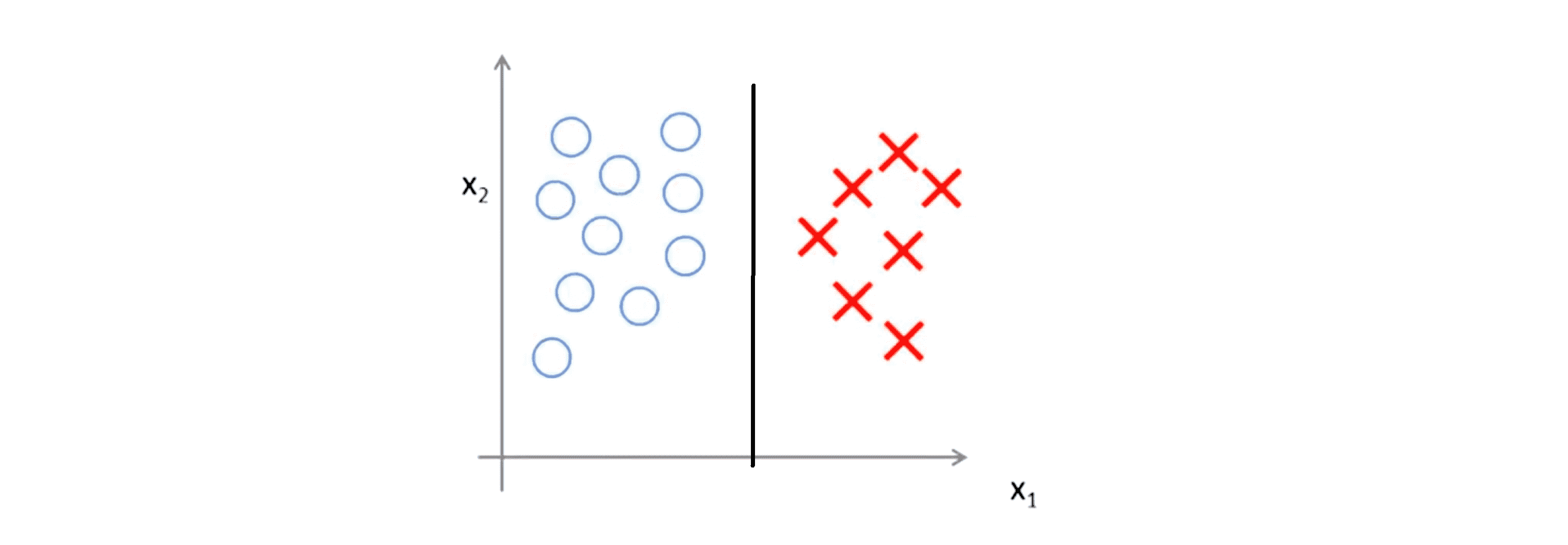
事实上支持向量机现在要比这个大间距分类器所体现的更激进，尤其是当你使用大间距分类器的时候，你的学习算法 会受异常点 (outlier) 的影响。比如我们加入一个额外的正样本，也许我最终会得到一条类似下图这样的新的决策界：

因为我们的 C 很大，所以仅仅基于一个异常样本，我们就将决策边界从这条黑线变到这条粉线，这实在是不明智的。但是如果 C 设置的小一点，则我们最终还是很大概率会得到这条黑线。当然数据如果不是线性可分的，如下图：

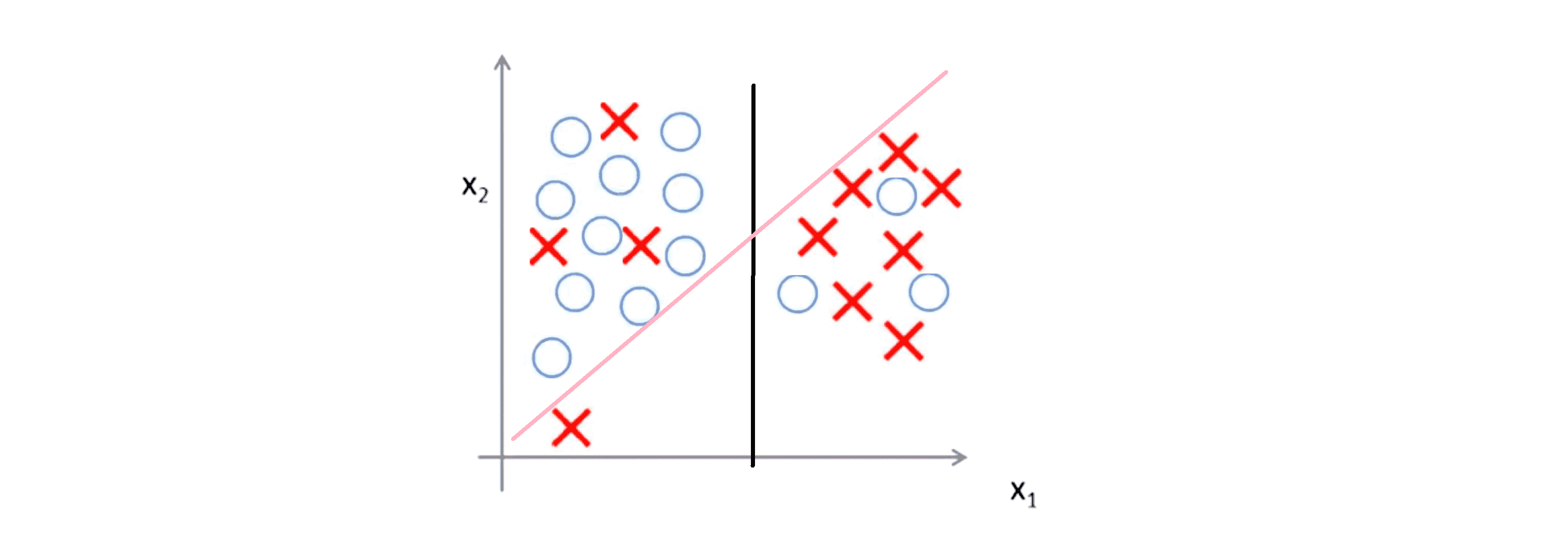
这时我们的逻辑回归可能就难以应付了，但是支持向量机却也会将它们恰当分开。所以当 C 不是非常非常大的时候，它就可以忽略掉一些异常点的影响得到更好的决策边界，甚至当你的数据不是线性可分的时候，支持向量机也可以给出好的结果。

大间隔的数学解释

在介绍大间隔的数学原理之前，让我们复习一下关于向量内积的知识。假设我有两个向量 u 和 v 都是二维向量，那么u^T * v就叫做向量 u 和 v 之间的内积。由于是二维向量，我们可以将它们画在这个图上：

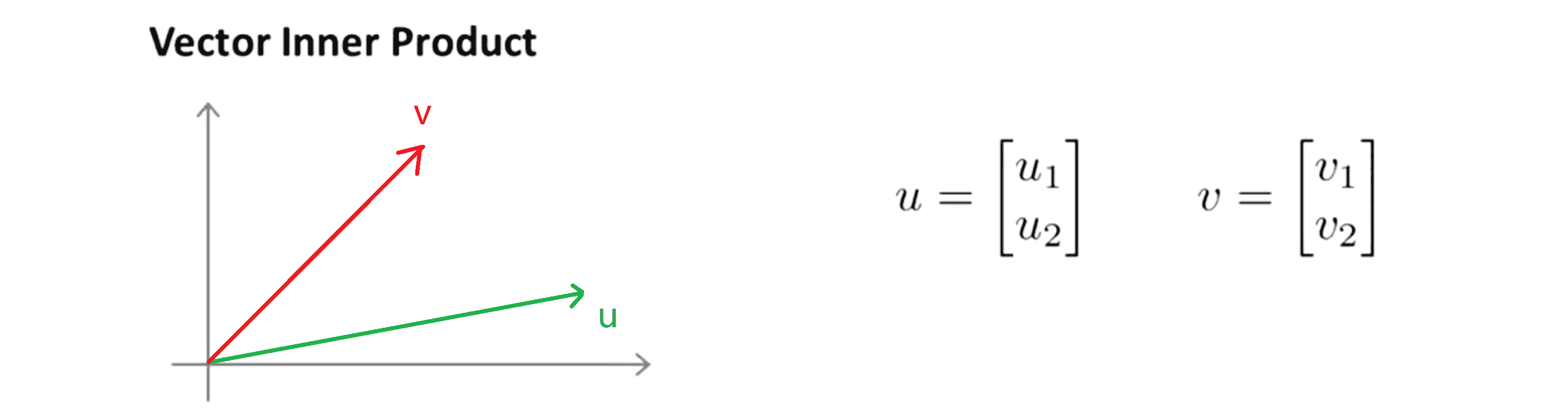
此时向量 u 的长度就是||u||， 此时向量 v 的长度就是||v||。现在让我们来看看如何计算 u 和 v 之间的内积，我们先将向量 v 直角投影到 向量 u 上，产生的新的向量我们称为 p ,设其长度为p'：

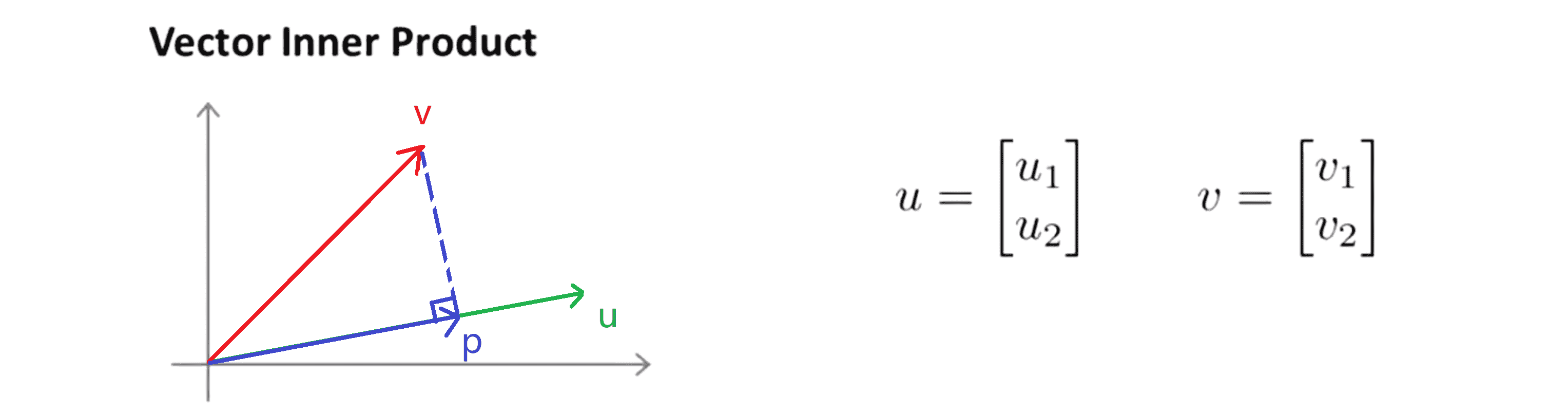
则其实u^T * v = p' * ||u||，同理我们发现将 u 和 v 交换位置将 u 投影到 v 上 而不是将 v 投影到 u 上，然后做同样地计算也能得到同样的结果。申明一点在这个等式中 u 的长度也就是||u||是一个实数，p'也是一个实数，但需要注意的就是 p' 事实上是有符号的，即它可能是正值也可能是负值。若 p 和 u 夹角为锐角，则 p' 为正， 反之 p' 为负。

我们接下来将会使用上面这些关于向量内积的性质来理解支持向量机中的目标函数的具体含义。下图的左边是我们先前给出的支持向量机模型中的目标函数，当C比较大时，我们代价函数的前一项就会很趋向0，所以只剩下后一项：

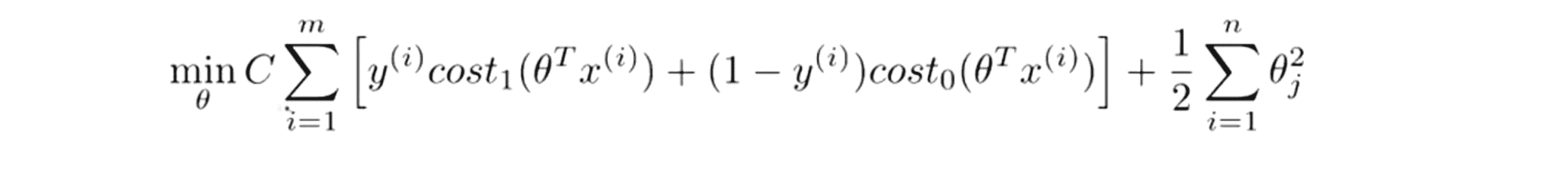
为了讲解方便，我们令 θ0 = 0 ，且特征数 n = 2. 现在我们来看一下支持向量机的优化目标函数，当我们仅有两个特征这个式子 θj^2 可以写作||θ||^2:

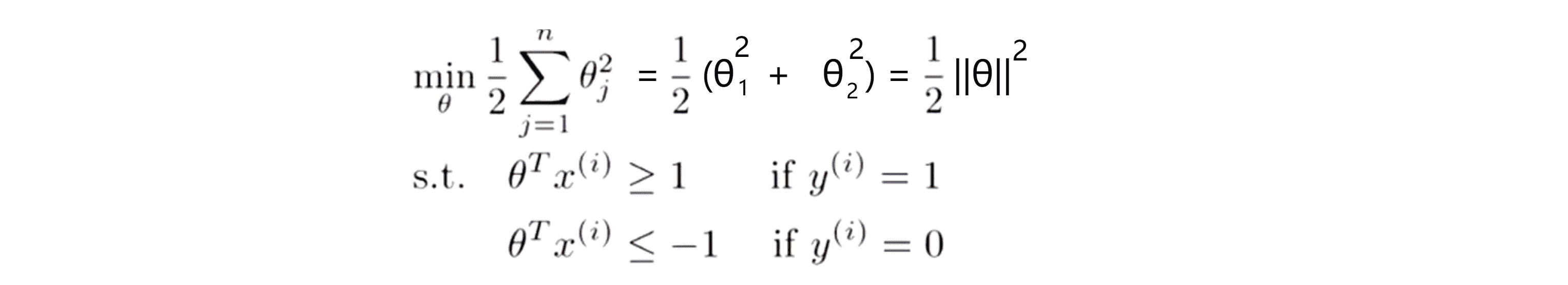
因此支持向量机做的全部事情就是极小化参数向量 θ 范数的平方,或者说长度的平方。现在我们给定参数向量 θ 再给定一个样本 x 会等于什么呢：

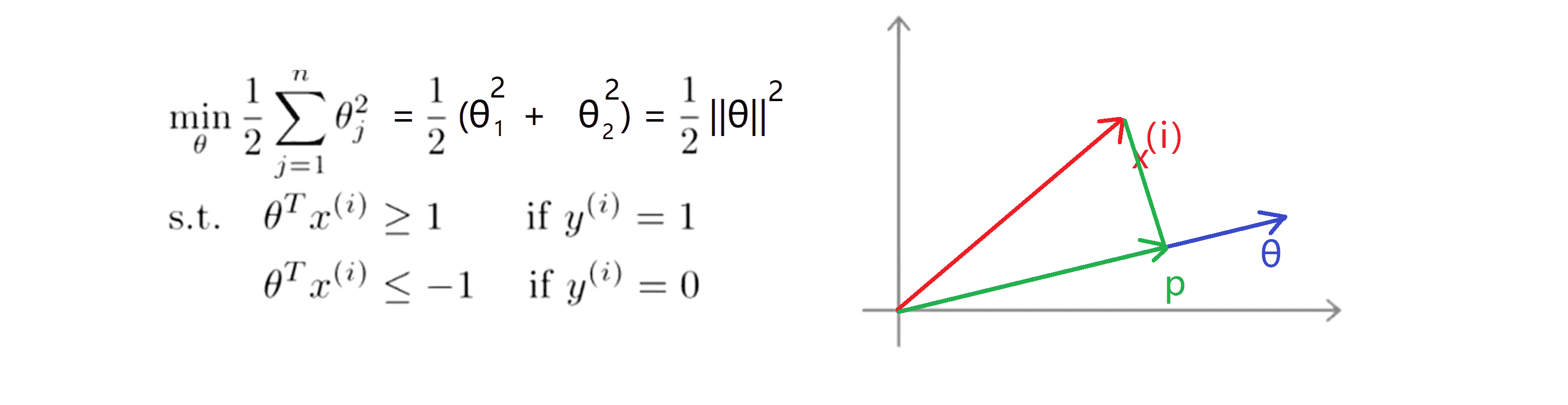
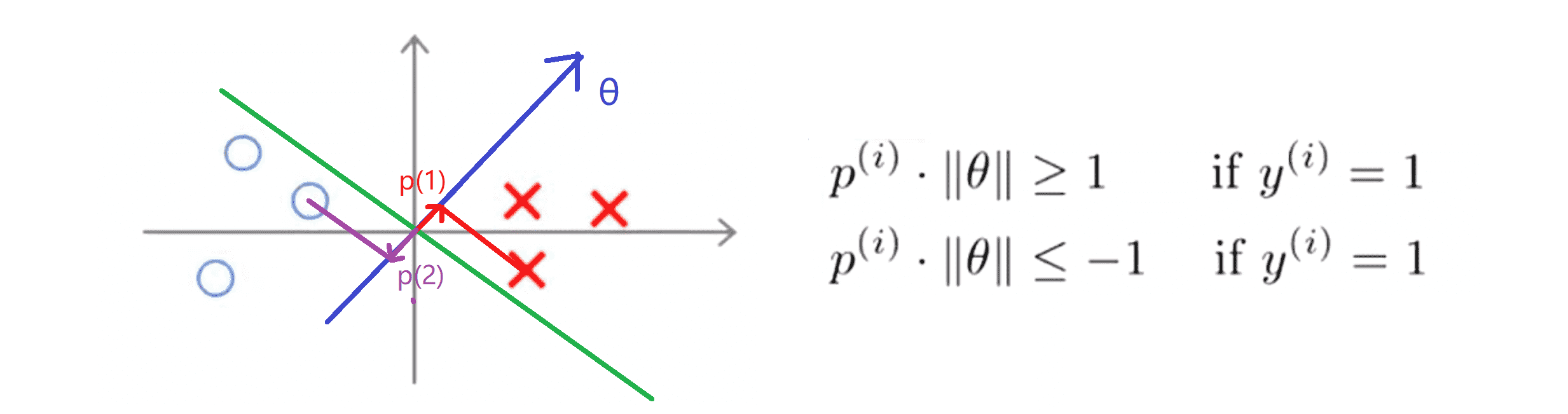
其实我们从之前内积的性质就知道，θ^T * x(i) = p' * ||θ||，其中p'就为向量p的带单位长度. 好这告诉了我们什么呢？这里表达的意思是这个 θ^T * x(i) ≥ 1 或者 θ^T * x(i) ≤ 1约束是可以被p' * ||θ|| ≥ 1 或者 p' * ||θ|| ≤ 1这个约束所代替的。所以为了让||θ||尽量的小，我们的p'就会尽量的大。这就是我们的优化目标——让p’尽可能大。

我们接着来看一下在这种优化条件下支持向量机会选择什么样的决策界。对于下图的样本例子，若我们假设支持向量机会选择下图绿线这个决策边界：

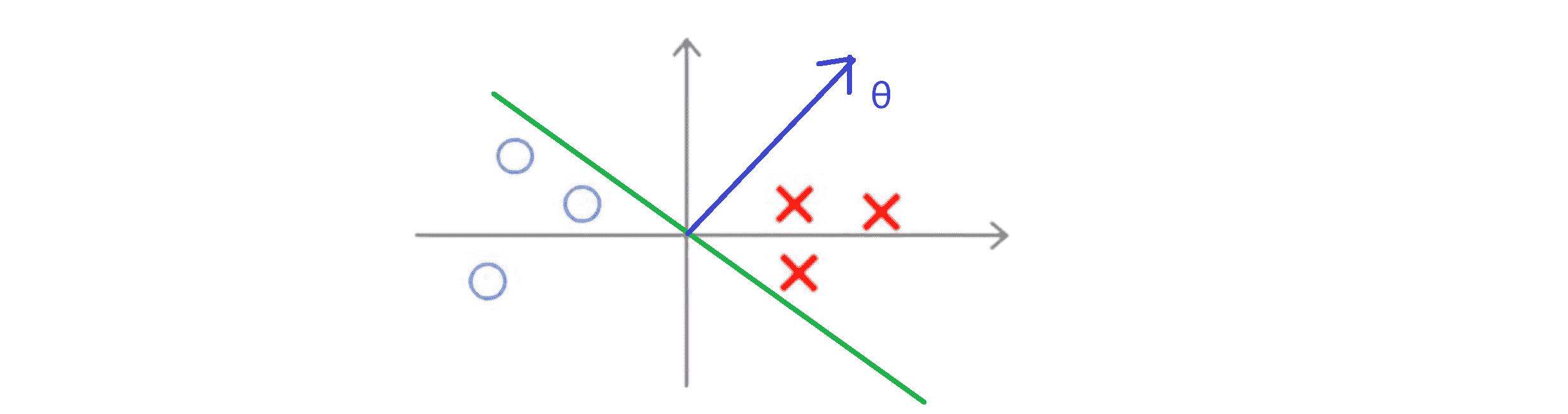
这显然不是一个非常好的选择，因为它的间距很小，这个决策界离训练样本的距离很近。那我们理性地来看一下为什么支持向量机不会选择它。对于这样选择的参数 θ，可以看到参数向量 θ 事实上是和决策界是90度正交的，因此这个绿色的决策界对应着一条蓝线代表参数向量 θ 。顺便提一句 θ0 等于 0 的简化仅仅意味着决策界必须通过原点 (0,0)。现在让我们看一下这条不太好的决策边界对于优化目标函数而言意味着什么：

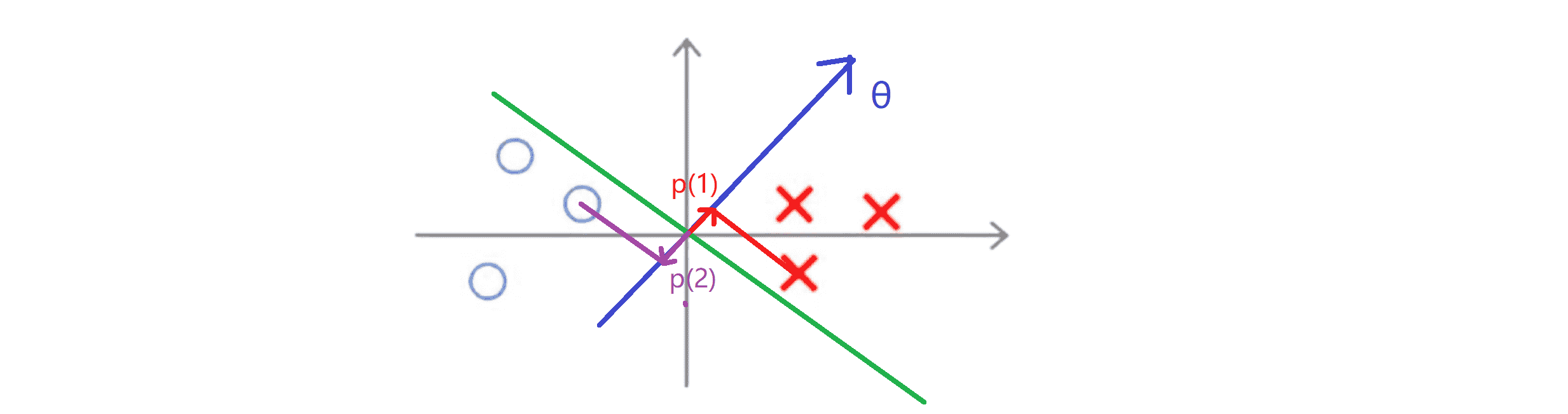
比如上图中右边这个样本，我们假设它是我的第一个样本 x(1) 如果我考察这个样本到参数 θ 的投影 p(1) ,就得到了一条短的红线段，其长度就等于p(1)'。类似地左边这个样本，设它是 x(2) ，则它到 θ 的投影就是那条紫色的短线段，记为 p(2) ，其长度为 p(2)'。这时我们会发现这些 p(i)' 将会是非常小的数，因此当我们考察优化目标函数的时候，对于正样本而言，我们需要p' * ||θ|| ≥ 1 ，但是如果像 p(1)' 一样非常小，那就意味着我们需要 θ 的范数非常大。类似地对于负样本而言，我们需要 p' * ||θ|| ≤ 1 而 p(2)' 会是一个非常小的数，因此唯一的办法就是 θ 的范数变大。但是我们的目标函数是 希望找到一个参数 θ 它的范数是最小的。因此这条决策边界看起来并不好：

相反的，我们来看一个另一个不同的决策边界。比如说支持向量机选择了下图绿色的这个决策界：

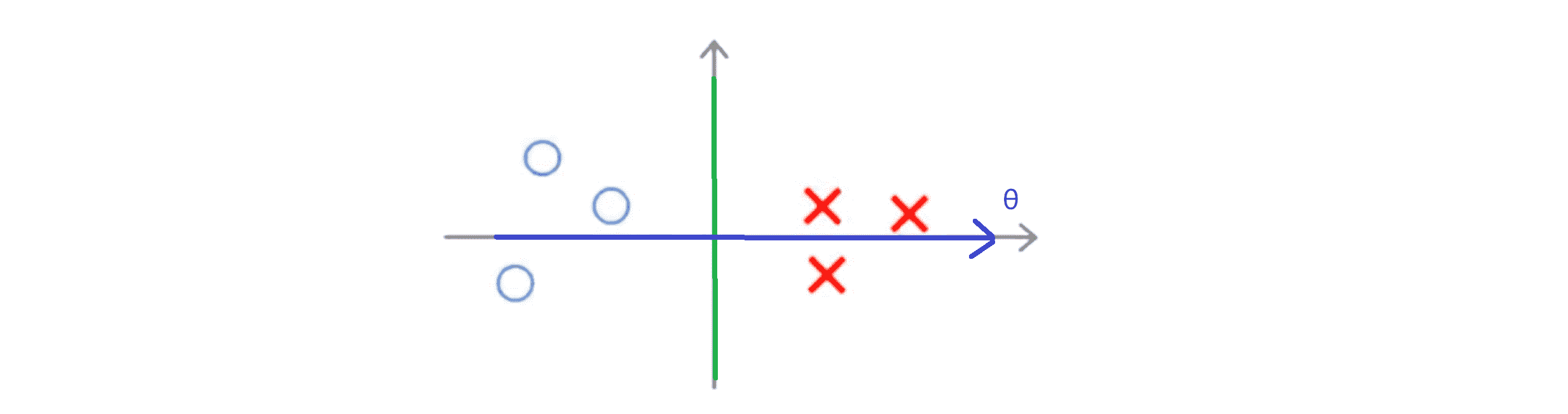
现在状况会有很大不同，我们一样正交得到θ。现在如果我们考察数据在横轴 x 上的投影，比如之前的两个样本样本 x(1) 和 x(2) ：

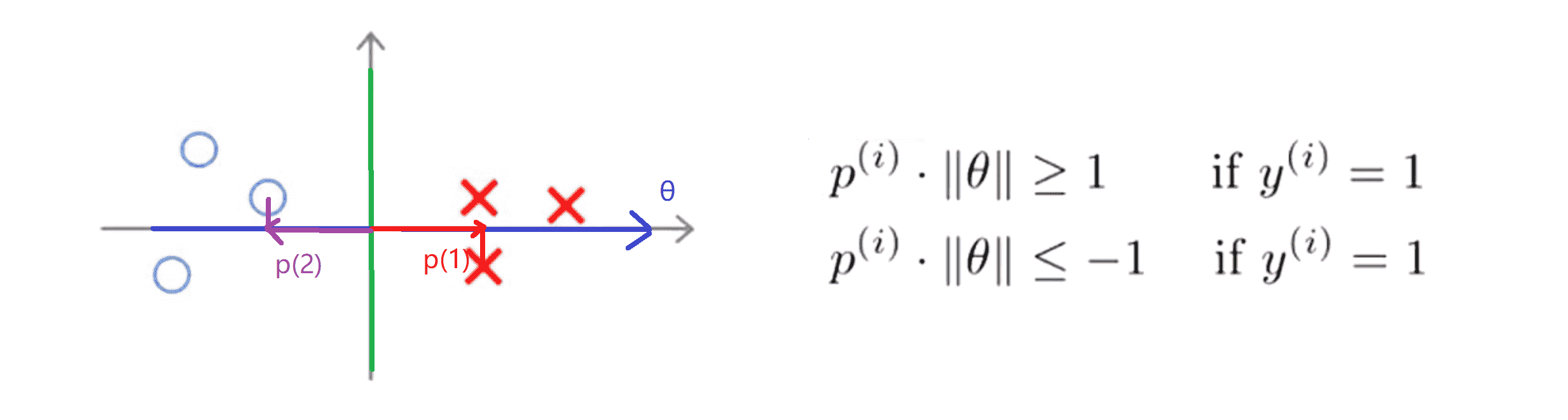
这时我们会注意到，现在 p(1)' 和 p(2)' 这些投影长度 是长多了，如果我们仍然要满足这些约束p' * ||θ|| ≥ 1 或者 p' * ||θ|| ≤ 1，则因为 p(1) 和 p(2) 变大了，所以 θ 的范数就可以变小了。因此这意味着通过选择现在的决策界而不是之前的那个，支持向量机可以使参数 θ 的范数变小很多。因此如果我们想令 θ 的范数变小，从而令 θ 范数的平方变小，就能让支持向量机选择现在的决策界。这就是支持向量机如何能有效地产生大间距分类的原因。

看我们后来那条决策边界那条绿线，我们希望正样本和负样本投影到 θ 的值大，要做到这一点的唯一方式就是选择后面这条绿线做决策界来区分开正样本和负样本。以上就是为什么支持向量机最终会找到大间距分类器的原因。因为它试图极大化这些 p(i) 的范数，它们就是训练样本到决策边界的距离。

最后一点我们的推导自始至终使用了这个简化假设，就是参数 θ0 = 0，就像我之前提到的这个的作用是让决策界通过原点，如果我们令 θ0 不是 0 的话，其含义就是我们希望决策界不通过原点。我们将不会做全部的推导，实际上支持向量机产生大间距分类器的结论会在 θ0 ≠ 0 时被证明同样成立，证明方式是非常类似的。

结语

通过这篇BLOG，相信你已经对SVM的大间隔有所了解。之后我们将会一起构建SVM算法。最后希望你喜欢这篇BLOG！