在之前的BLOG中,我们一同学习了监督学习中的回归问题及其解法。在接下来的几篇BLOG中,我们将着眼于监督学习中的另一块内容-分类问题进行学习。
分类问题
首先,先让我们回顾一下分类问题。什么是分类问题?此前我们谈到的过电子邮件垃圾邮件分类就是一个经典的分类问题;而网上交易,比如一个交易的网站是不是欺诈网站也是分类问题;还有我们经常提到的,判断一个肿瘤是否是良性的也是分类问题。
我们想要预测的变量 y 一般的取值是 0 或 1 ,后面我们也会提到更多取值的分类问题,但为了简化问题,下面我们以y 一般的取值是 0 或 1的分类问题为例。
一般,对于 y,其取值为 0 时我们称其为负样本(Negative Class),其取值为 1 时我们称其为正样本(Positive Class)。

那我们如何解决分类问题呢?让我们先来看一个训练集,这个训练集是用来给肿瘤分类为 恶性或者良性的。注意这个是否恶性只能取两个值,0也就是非(恶性) 和 1 也就是是(恶性):
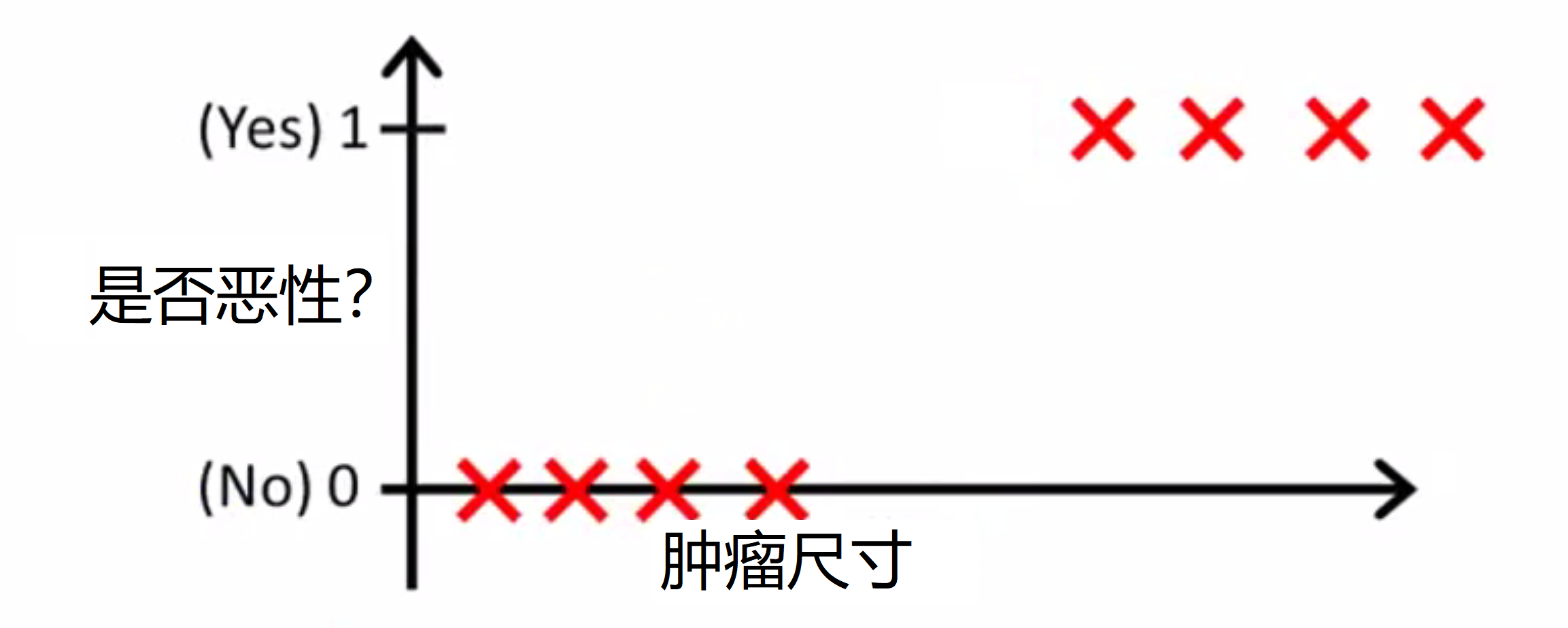
我们能否使用已经学过的线性回归用于这组数据来尝试用一条直线来拟合数据呢?我们来操作看看。如果用一条直线拟合这个训练集,我们就会得到下图这样的假设函数 h(x) = θ^T * x:

我们的目标是对肿瘤是否恶性进行分类,所以我们可以尝试将分类器的输出阈值设为0.5,如果假设输出的值大于等于 0.5我们就预测 y 值等于 1,也就是恶性,如果小于0.5 我们预测 y 等于 0,也就是良性:

所以在我所绘的红线左侧的所有点,都会被预测为良性,而右边的点都会被预测为恶性。在这个特定的例子中看起来好像线性回归所做的是合理的,那是不是就代表我们可以完全用线性回归去解决分类问题呢?
现在让我们把训练集稍微改一下,我们稍微延长一下横轴,然后新增一个训练样本在很远的右边那里。注意这个额外的训练样本直观看来对我们的主观预测实际上并没有改变什么,因为它的尺寸太大了,肯定是恶性的:
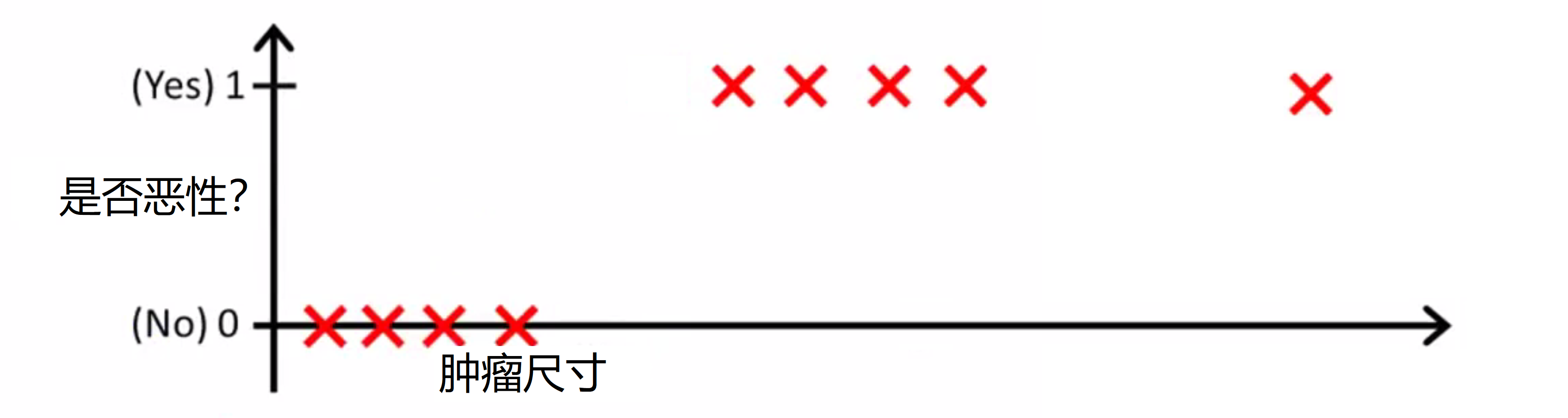
但是由于这个数据的加入,我们的对所有数据拟合的回归直线就发生的偏差,变成了绿色的直线:

我们再将 y 等于 0.5作为分界线进行预测,这时我们就发现问题了——因为一个看起来没什么影响的数据加入,导致我判断的红线发生了右移,导致了本来就为恶性肿瘤的一些数据被我判成了良性。而且我们还发现,其实 y 的取值只可能是 0 或 1,但使用线性回归,我们对 y 的预测会出现大于 1 或者小于 0 的情况,这应该是不允许的。
所以其实在大多数情况下,直接用线性回归算法去解决分类问题是不太可取的,所以在此我们就要学习一种新的模型来解决分类问题-逻辑回归。
逻辑回归
让我们开始谈谈逻辑回归,首先让我们一起看看假设函数的表达式,也就是说在分类问题中我们要用什么样的函数来表示我们的假设函数。
之前提到过,我们希望我们假设函数的输出值在0和1之间,因此我们希望得出一个满足这个性质的假设函数。当我们使用线性回归的时候,假设函数一般是 h(x) = θ^T * x.对于逻辑回归来说,我们只需要在外面再套一层函数,把假设函数改成 h(x) = g(θ^T * x) 其中定义函数g如下: 当z是一个实数时,我们有g(z) = 1/(1 + e^(-z)) ,这称为 S 型函数 (sigmoid function) 或逻辑函数(logic function)而两个术语基本上是可互换的,我们使用哪一个术语都可以,我们把上面两个式子写到一起就有h(x)=1/(1+e^(-θ^T * x)) :
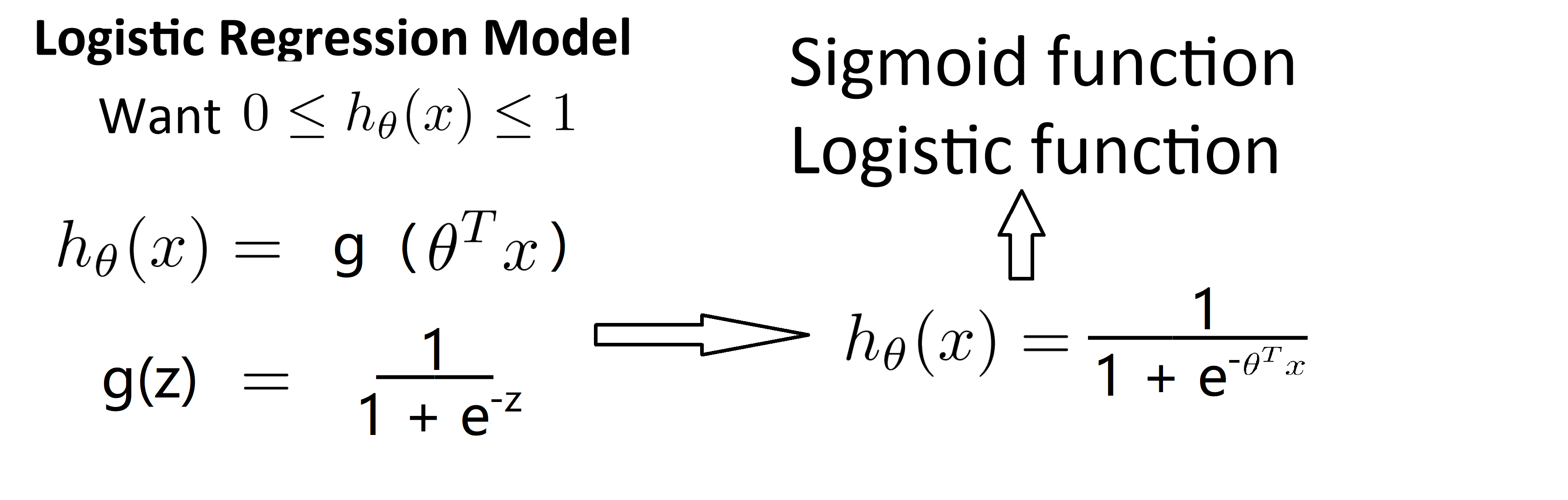
然后我们看一下g(z)也就是S型函数是什么样的,如下图:
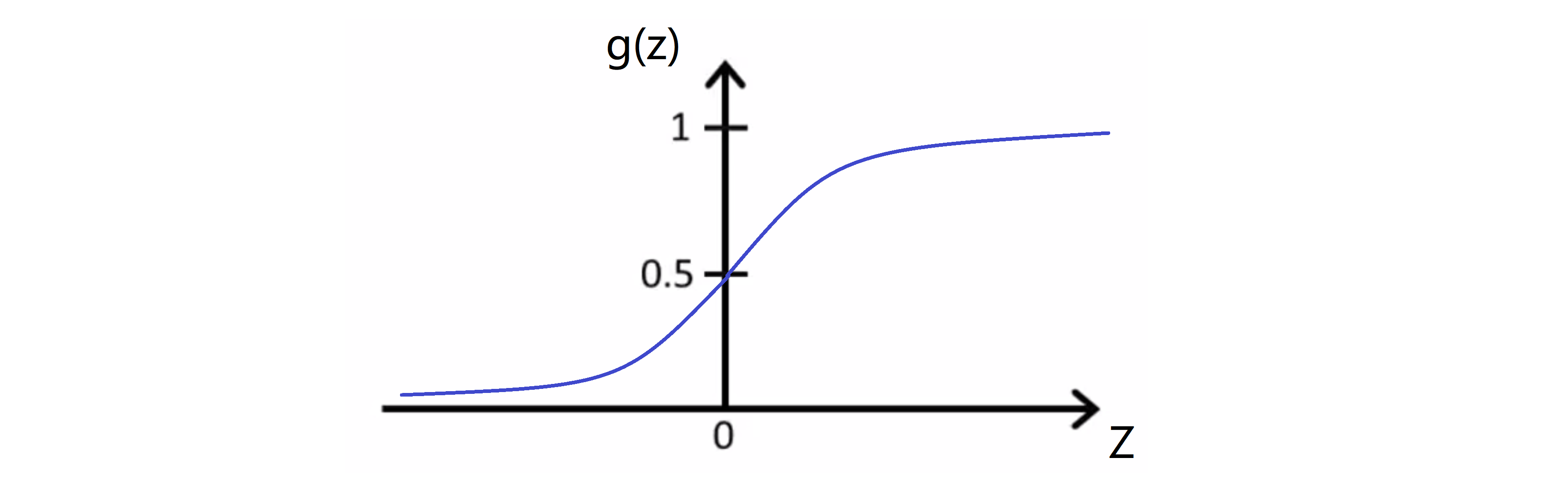
这就是S型函数大概的样子。注意S型函数,当 z 趋向于正无穷的时候,g(z)趋向于于1;然后随着横坐标趋向于 0 ,g(z)趋向于 0.5;最后当 z 趋向于负无穷的时候,g(z)趋向于于0。因此 g(z) 的取值一直在0和1之间符合我们的要求。
对于这个假设函数,我们需要做还是和之前一样,就算用参数θ拟合我们的数据。所以对于一个训练集,我们需要给参数 θ 选定一个值,然后用这个假设函数做出预测。之后我们将一同学习一个用来拟合参数 θ 的学习算法。但是首先让我们讨论一下这个模型的具体含义。
其实假设函数 h(x) 的输出的含义当我的假设函数输出某个数,我就会认为这个数是对于新输入样本 x 当 y 等于 1 时的概率的估计值。举个例子吧,比方说肿瘤分类的例子,我们有一个特征向量 x 包含 x0 和 x1,和平时一样 x0 恒等于 1 且 x1 是肿瘤的大小,假设我有一个病人来了,告诉了我们他肿瘤的大小 x1,我们把他的特征向量 x 代入我的假设函数,假如假设函数的输出为0.7:
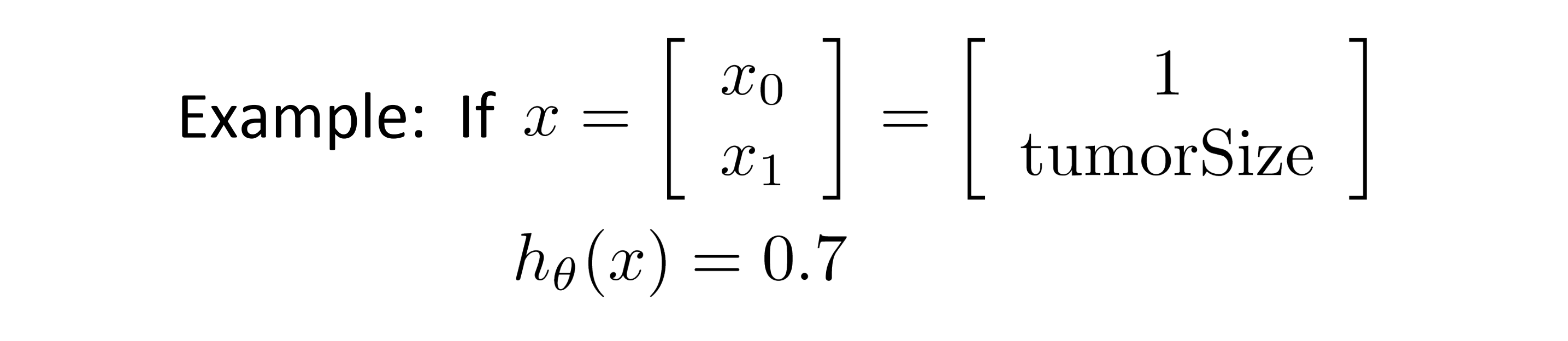
这时其含义就是,对于一个特征为 x 的患者,其 y 等于 1 的概率是0.7。换句话说我要告诉我的病人,非常遗憾,你的肿瘤是恶性的可能性是70%。具体来说我的假设函数h(x) = P(y=1|x;θ)。因此 有了 h(x) 我们也可以计算 y = 0 的概率,因为我们知道 y = 0 的概率加上 y = 1 的概率一定会等于1,所以我们有:

这样我们就可以求出y = 0的概率。
逻辑回归的直观认识
我们现在已经知道了逻辑回归的假设函数的表达式是什么,耶逻辑回归的假设函数的表达式是什么。接下来就让我们通过例子对假设函数是什么样子有一个更直观的认识,来让我们更好地理解逻辑回归的假设函数到底是什么样子的。顺便也一同学习一个叫做决策边界(decision boundary)的概念,这个概念也能更好地帮助我们理解逻辑回归的假设函数在计算什么。
让我们看看刚刚写下的公式:

现在让我们更进一步来理解这个假设函数何时会将 y 预测为 1,又在什么时候又会将 y 预测为0。我们知道这个假设函数输出的是给定 x 对应的 y = 1 的概率,因此如果我们想预测y = 1 还是 y = 1,我们可以这样做:当该假设函数输出 y = 1 的概率大于或等于0.5时,那么这表示 y此时更有可能等于 1 而不是 0, 因此我们预测y = 1;相反地,如果预测 y = 1的概率小于0.5,那么我们就应该预测 y = 0。在上面我用了大于等于,但其实如果 h(x) 的值正好等于 0.5,我即可以预测其为 1 ,也可以预测其为 0。但是在这我们默认如果h(x)等于 0.5 的话,就预测选择为 1,这只是一个小细节,不用太在意。
下面我们来看看什么时候g(z) 将大于或等于 0.5 从而最终预测 y = 1。如果我们看看h(x)对应的下图的S形函数的曲线图,我们会注意到对于S形函数,只要z大于等于0的时候,g(z)就会大于等于0.5:

所以在纵轴的右半边g(z)大于或等于0.5,左半边g(z)小于0.5,且 z = 0时,h(z) = 0.5。我们注意到假设函数h(x) = g(θ^T*x) 因此我们有θ^T*x≥0时,h(x)≥0.5,θ^T*x<0时,h(x)<0.5:

我们来举个例子吧。现在假设我们有一个训练集,我们的假设函数是 h(x) = g(θ0 + θ1 * x1 + θ2 * x2):
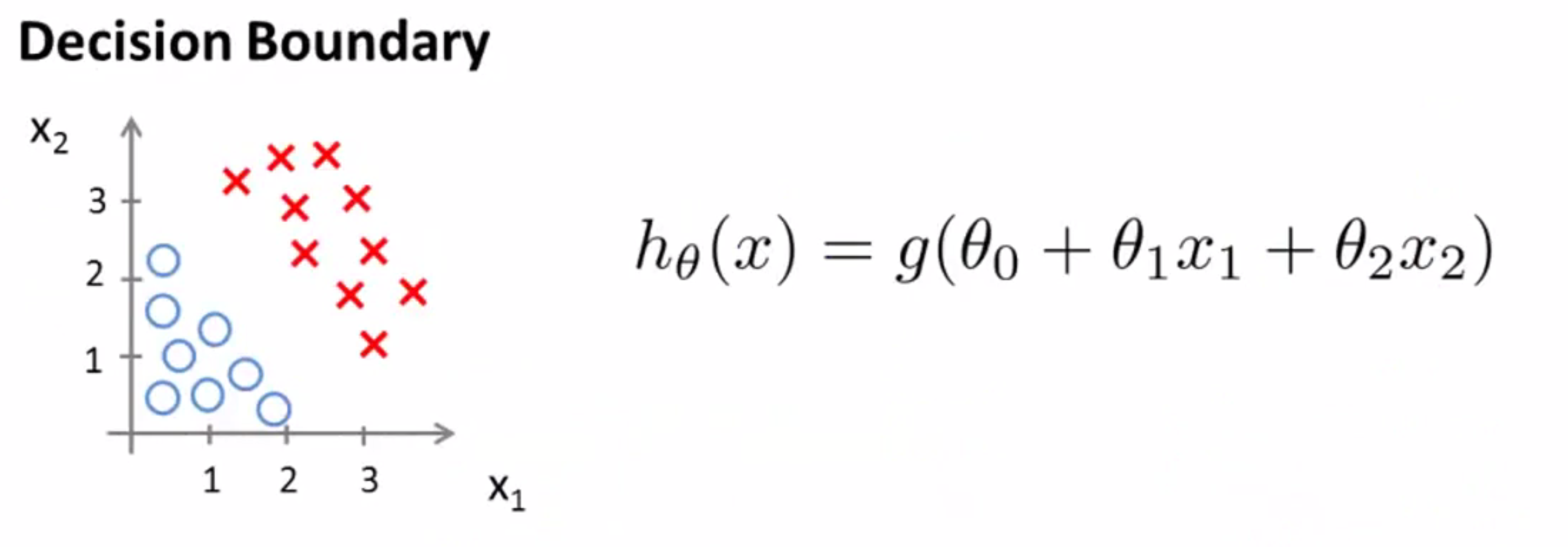
目前我们还没有谈到如何拟合此模型中的参数θ,但是假设我们已经拟合好了参数,比方说θ0 = -3,θ1 = 1,θ2 = 1,因此 θ 等于[-3 1 1]。这样我们有了一个参数选择,让我们试着找出假设函数何时将预测 y 等于 1 ,何时又将预测 y 等于0。根据之前的公式,我们知道要 y = 1的概率大于等于0.5,就要 θ^T*x > 0,具体到这里也就是要 θ0 + θ1 * x1 + θ2 * x2 > 0,代入θ,-3 + x1 + x2 > 0。
我们发现,这一假设函数将预测 y = 1 只要 x1 + x2大于等于3就可以了,让我们来看看这在图上是什么意思:
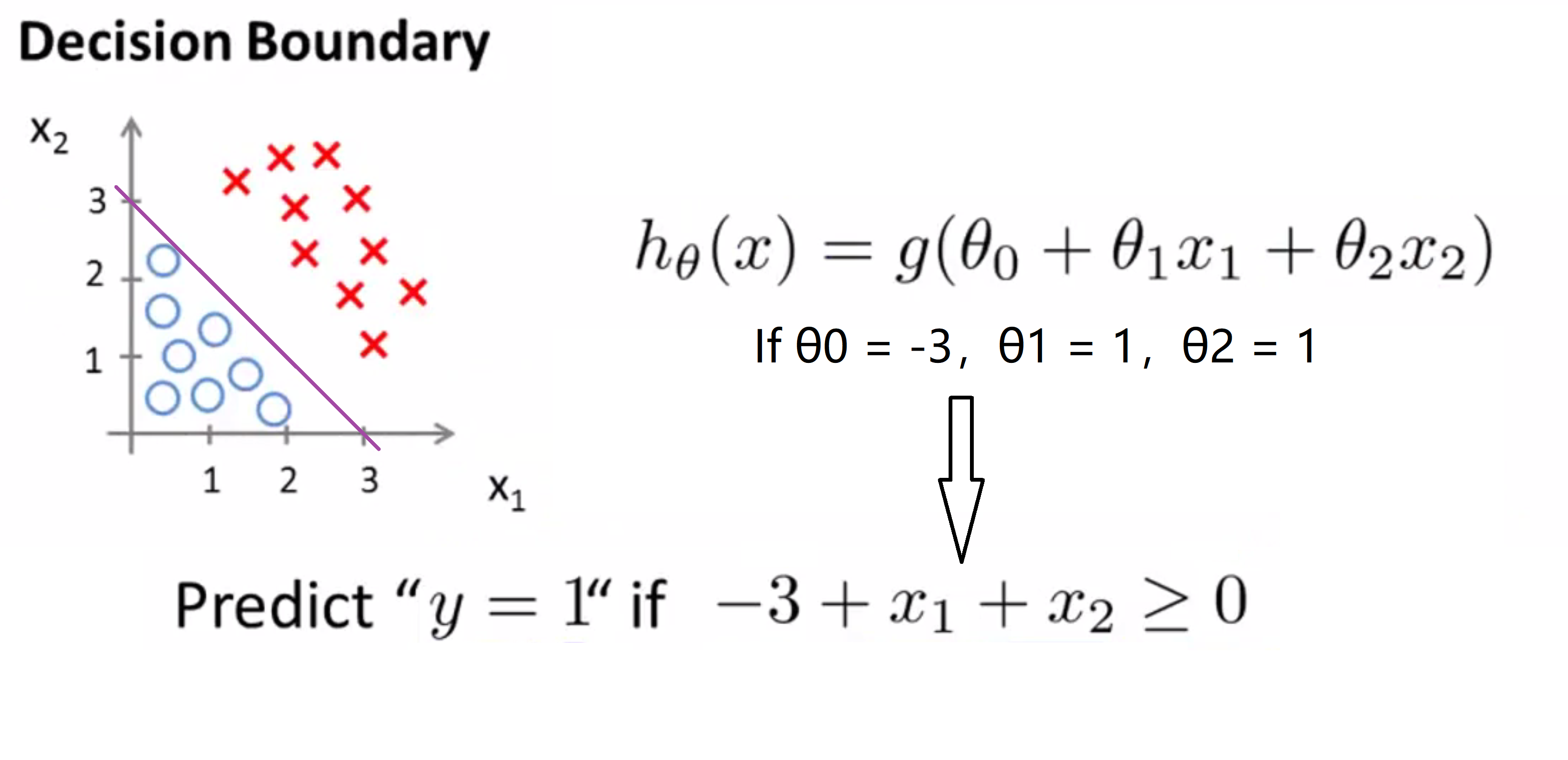
如果我写下等式 x1 + x2 = 3,这将定义一条直线,即上图中紫色的那条直线。而对于这条直线上方,也就是很多红色X的地方,就是我们预测 y = 1 的区域,与此相对,这条直线的下方,也就是很多蓝色的O的区域,就是我们的假设函数预测y = 0的区域。
我想给这条线一个名字,其实这条线就被称为决策边界(decision boundary),具体地说这条直线满足x1+x2=3 所对应一系列的点,它对应 h(x) 等于 0.5的区域。决策边界也就是这条直线将整个平面分成了两部分,其中一片区域假设函数将预测y = 1,而另一片区域假设函数将预测y = 0。要注意,决策边界是假设函数的一个属性,它只与参数θ有关,与训练集没有直接的关系。一旦我们从训练集得到确定的参数取值θ我们就将完全确定决策边界。这时其实我们实际上并不需要在绘制决策边界的时候绘制训练集,只需要照着图对输入的x进行预测就行了。
现在让我们看一个更复杂的例子。和往常一样,我使用交叉 (X) 表示我的正样本,圆圈 (O) 的表示我的负样本 给定下图这样的一个训练集,我怎样才能使用逻辑回归拟合这些数据呢?
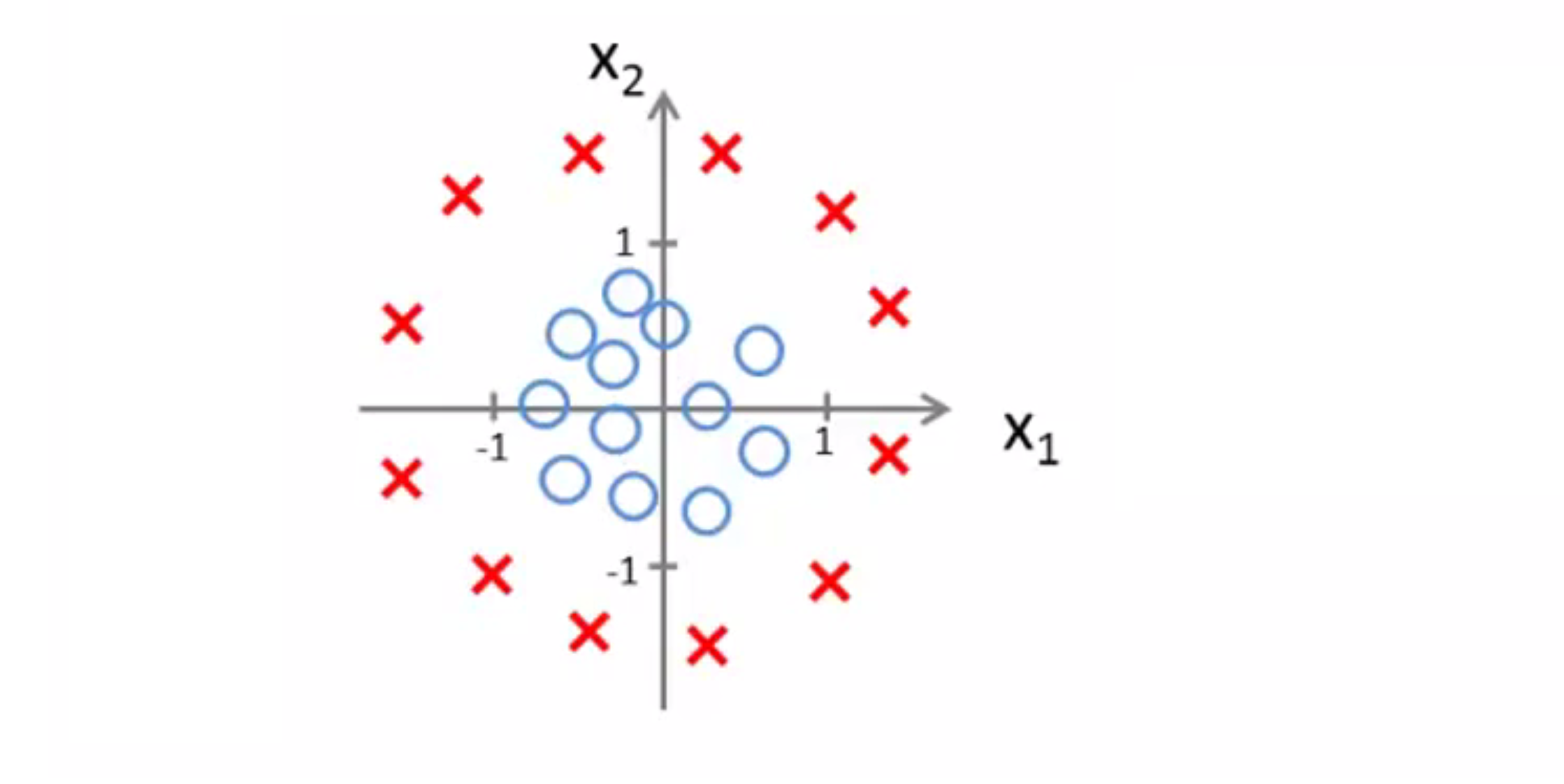
早些时候我们讨论过多项式回归,我们谈到可以添加额外的高阶多项式项来拟合数据,同样我们也可以对逻辑回归使用相同的方法,具体地说我们的假设函数是这样的:h(x) = g(θ0 + θ1 * x1 + θ2 * x2 + θ3 * x1^2 + θ4 * x2^2),所以我现在有5个参数 θ0 到 θ4。我们会在之后的BLOG谈论到参数θ0到θ4的取值方法, 但是假设现在我已经使用了这个方法得到θ0 = -1,θ1 = 0,θ2 = 0,θ3 = 1,θ4 = 1,即θ = [-1 0 0 1 1]。根据我们前面的讨论,这意味着我的假设函数将预测 y = 1 只要-1 + x1^2 +x2^2 ≥ 0,即只要x1^2 +x2^2 ≥ 1:
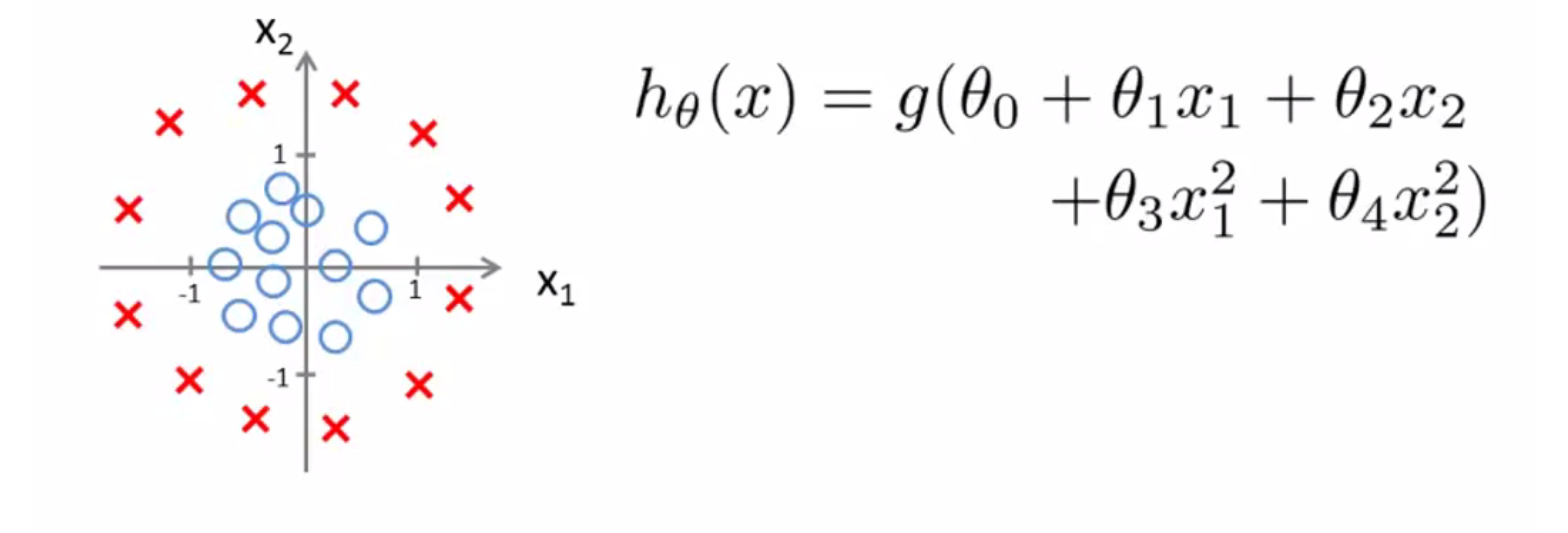
那么这时我们的决策边界是什么样子的呢?其实这个方程就对应半径为1,圆心为原点的圆:
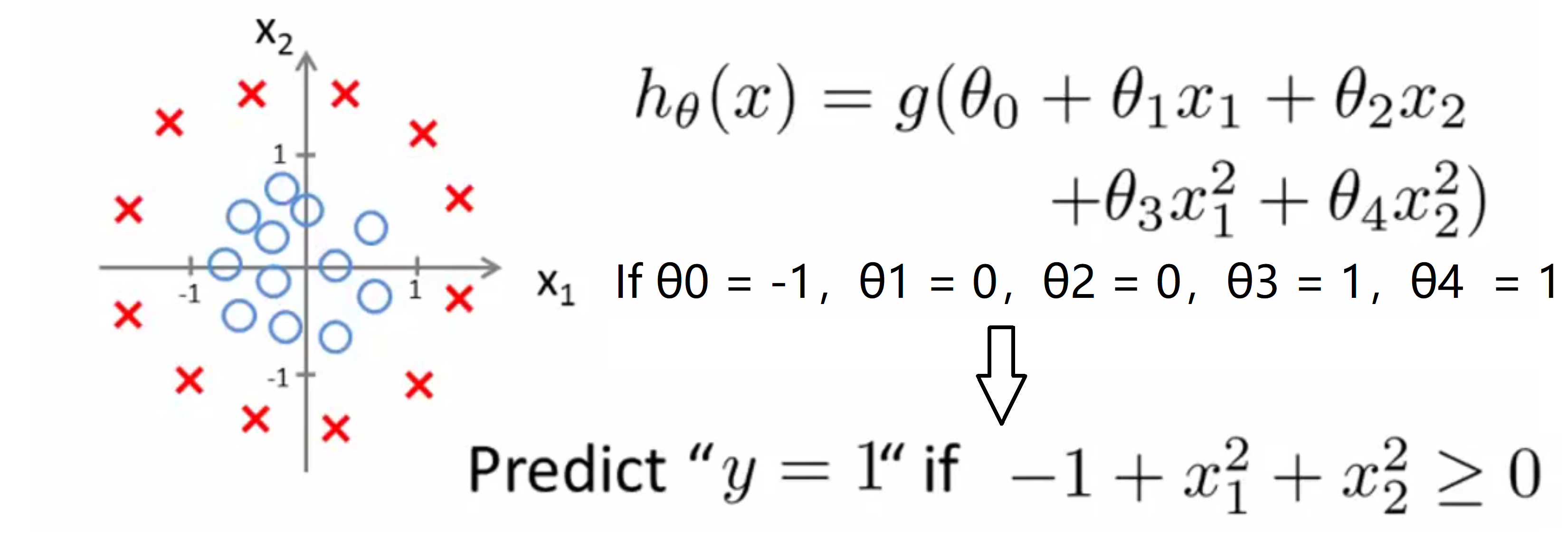
所以,上面绿色的圆就是我们的决策边界,圆外面的一切 我将预测 y = 1,而在在圆内的一切我会预测y = 0。因此通过增加这些复杂的多项式特征变量我可以得到更复杂的决定边界,而不只是用简单直线分开正负样本。
最后让我们再来看看一个更复杂的例子,我们可以得到更复杂的决策边界吗?其实是可以的。如果我有高阶多项式特征变量,如下,我可能可以得到一些更加千奇百怪的形状:
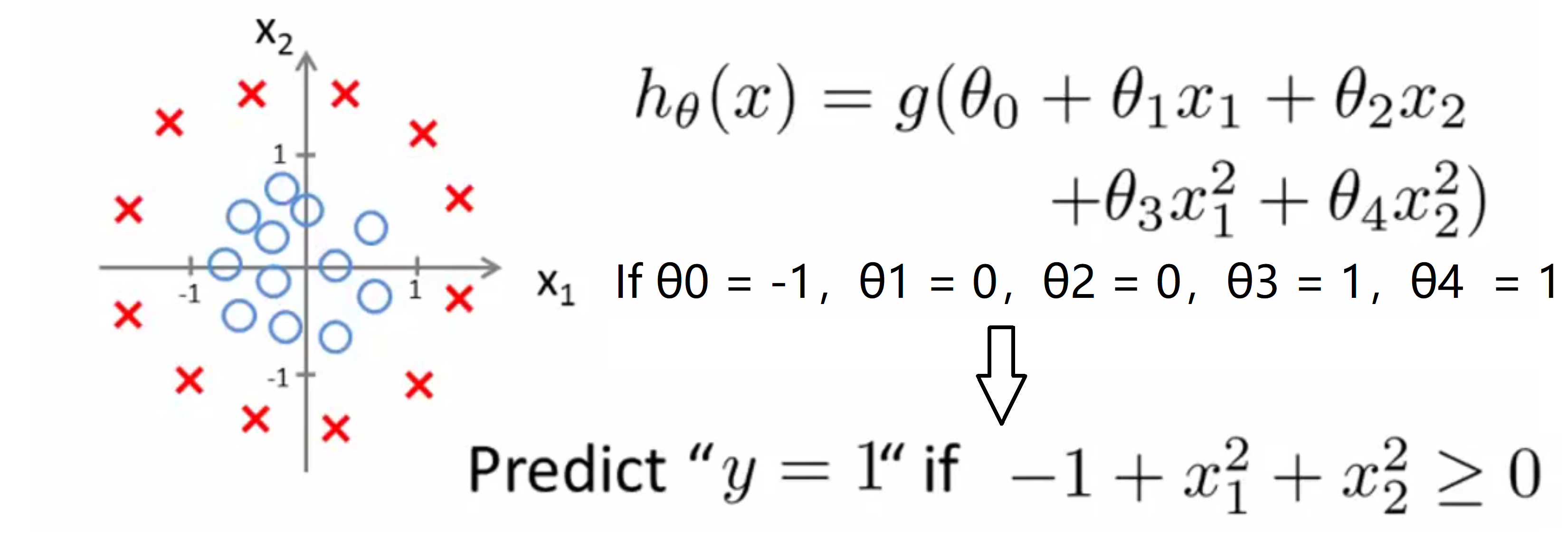
因此通过这些可视化图形,我希望告诉你什么范围的假设函数我们可以使用来表示逻辑回归。
结语
通过这篇BLOG,相信你已经对分类问题和逻辑回归有了一定的认识。在之后的BLOG中,我们将会继续学习一种得到参数 θ 的算法。最后希望你喜欢这篇BLOG!