在之前的BLOG里，我们介绍了机器学习的一些基本概念，在这篇BLOG中，就让我们学习一下监督学习中经典的单变量线性回归算法吧！

线性回归模型

我们第一个学习算法是线性回归算法。让我们通过一个例子来开始，这个例子是预测住房价格的，我们要使用一个包含俄勒冈州波特兰市的住房价格的数据集：

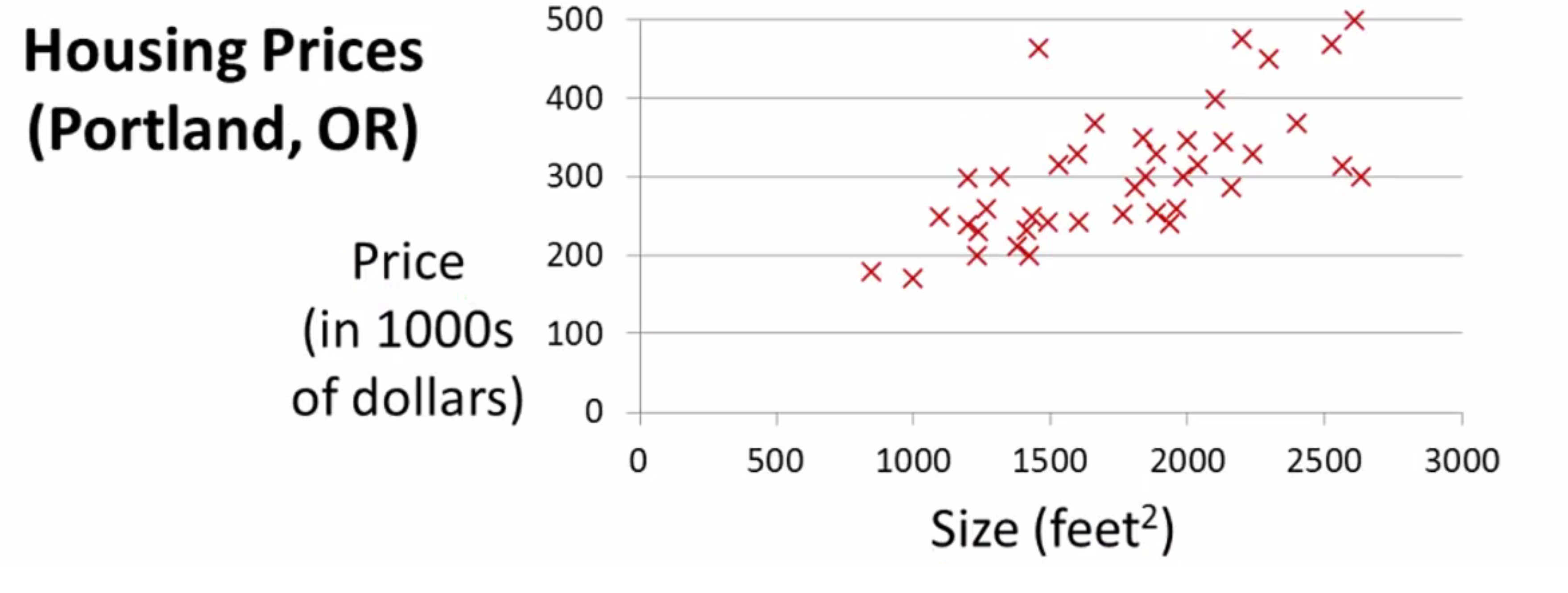
这时假如你有一个朋友正想出售自己的房子，其大小约是1250平方尺大小，你想要告诉他这房子能卖多少钱。那么你可以做的一件事就是构建一个模型比如如下的这条直线，从这个数据模型上来看 也许你可以告诉你的朋友 他能以大约220000(美元)左右的价格卖掉这个房子，这就是监督学习算法的一个例子。

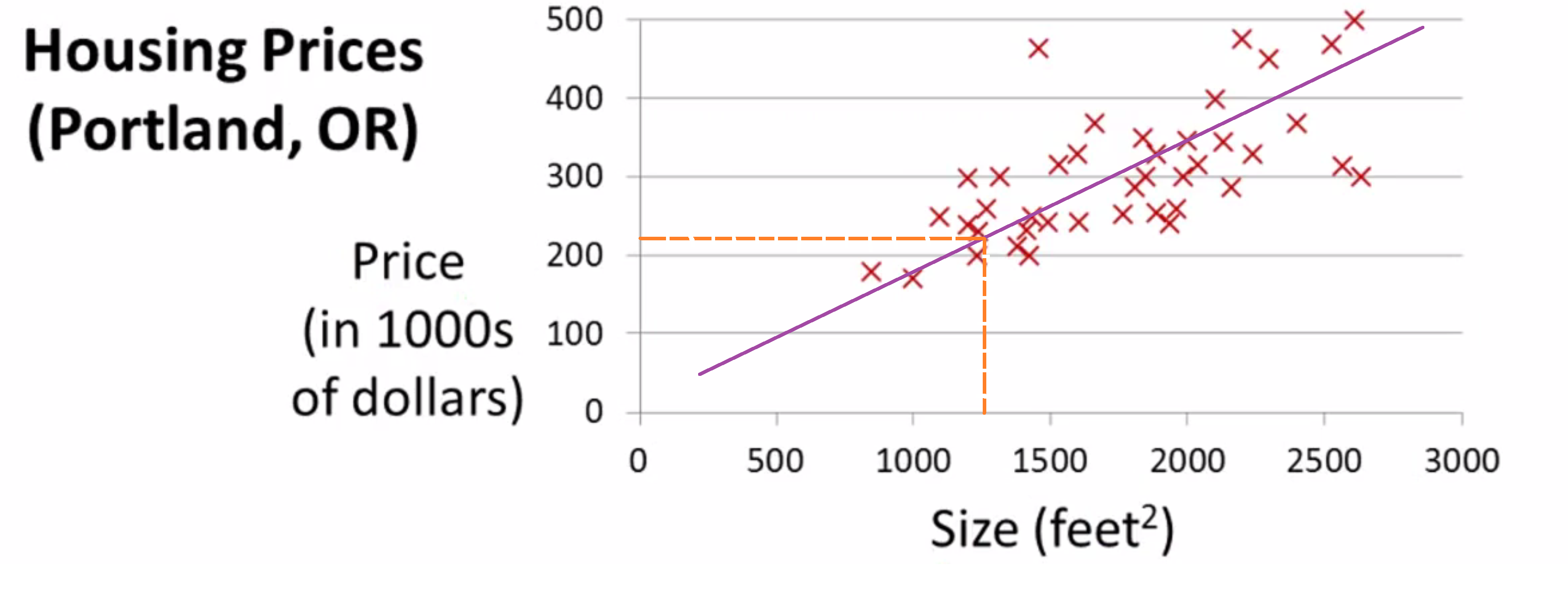
它被称作监督学习是因为对于每个数据来说，我们给出了 “正确的答案” ；更具体来说，这是一个回归问题，回归一词指的是我们根据之前的数据预测出一个准确的输出值，对于这个例子就是价格。同时，还有另一种最常见的监督学习方式叫做分类问题。当我们想要预测离散的输出值，例如寻找癌症肿瘤并想要确定 肿瘤是良性的还是恶性的，这就是0/1离散输出的问题。

更进一步来说 在监督学习中我们有一个数据集,这个数据集被称训练集，因此对于房价的例子，我们有一个训练集包含不同的房屋价格，我们的任务就是从这个数据中学习预测房屋价格:

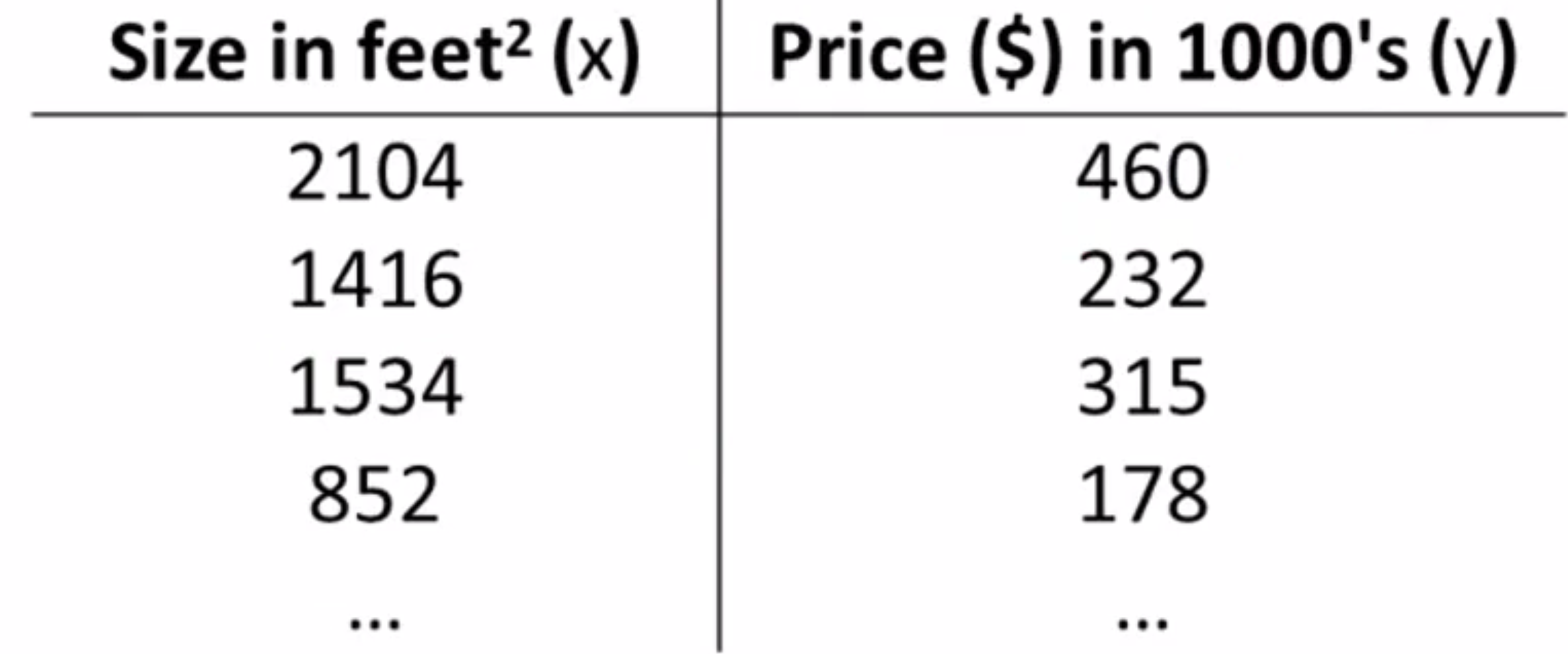
现在我们给出这门课中经常使用的一些符号定义：

1.m:表示训练样本的数目。因此,假如在上面的这个数据集中，如果表中有47行，那么我们就有47组训练样本，m就等于47。
2.x：表示输入变量，其往往也被称为特征量，也就是用x表示输入的特征。
3.y：表示输出变量或者目标变量，也就是我的预测结果。
4.(x, y)：表示一个训练样本，所以在这个表格中的每一行都对应于一个训练样本，为了表示某个训练样本，我将使用x上标(i)与y上标(i)来表示 ，所以(x(i), y(i)) 括号里的上标i表示训练集里的第i行。

举个例子在上述训练集中，x(1) 指的是 第2104这个输入值 ，x(2)则等于1416。以下就是一个监督学习算法的工作方式：

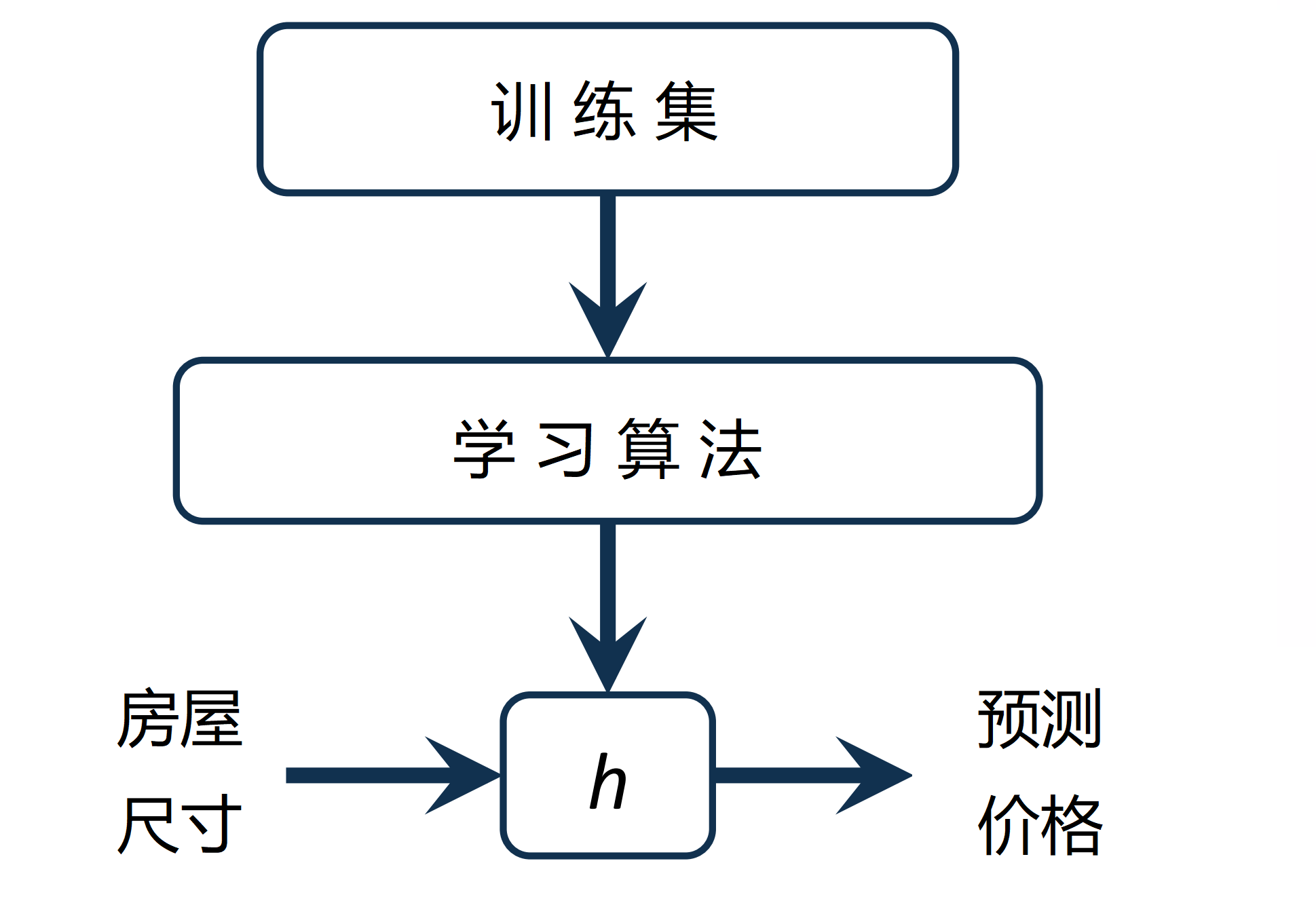
我们可以看到我们把训练集里房屋价格喂给我们的学习算法，然后输出一个函数，按照惯例，这个函数通常表示为小写 h ， h 代表hypothesis(假设)。 h 表示一个函数，输入房屋尺寸大小，就像你朋友想出售的房屋后， h 根据输入的 x 值来得出 y 值，而y值对应房子的价格。因此 h是一个从 x 到 y 的函数映射。

我们我们将一个线性回归方程写为 hθ(x)=θ0+θ1*x 为了方便 有时非书面形式也可以将写 hθ(x) 写成h(x)，这是一种缩写方式，但一般来说都会保留这个下标θ。

我们的目标是要预测一个关于x的 线性函数 y 对吧? 我们要用数据集来预测y关于x的线性函数 hθ(x)=θ0+θ1*x。那么为什么会是一个线性函数呢? 有时候，我们会有更复杂的函数，也许是非线性函数，但是由于线性方程是简单的形式，我们通常将先从线性方程的例子入手，当然最终我们将会建立更复杂的模型，以及更复杂的学习算法。让我们也给这模型起一个名字——其实这个模型被称为线性回归(linear regression)模型。另外，这实际上是关于单个变量的线性回归，而这个变量就是x，我们只根据x来预测y。同时对于这种模型有另外一个名称，称作单变量线性回归，单变量是对一个变量的一种特别的表述方式。

以上就是线性回归模型的一些基本知识。

代价函数数学定义

我们如何让我们的线性方程与我们的数据相拟合？或者说，如何判断一条直线和数据的拟合程度？这就要用到代价函数。

假如在线性回归中我们有一个像这样的训练集：

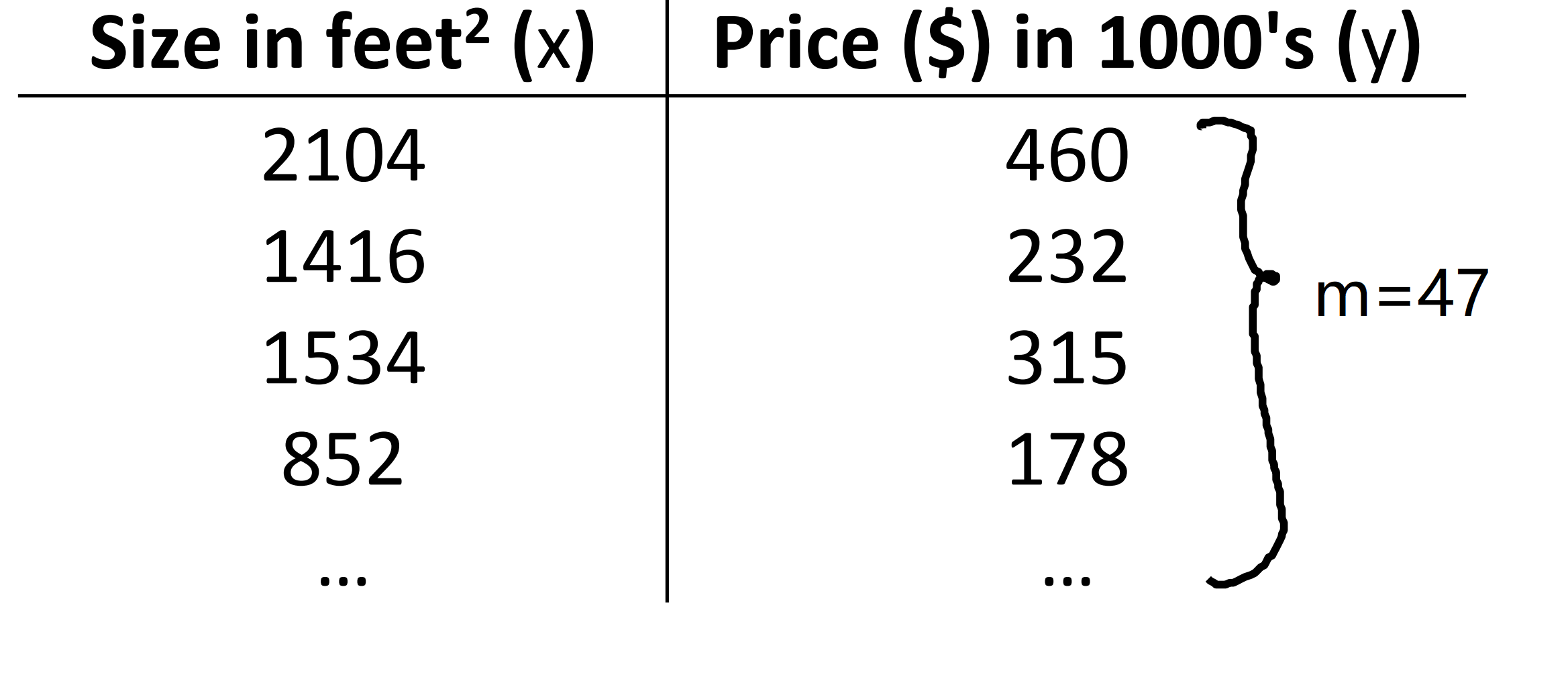
其中训练集规模m = 47。而我们的假设函数， 也就是用来进行预测的函数，是这样的线性函数形式——hθ(x)=θ0+θ1*x。我们把θi我称为模型参数，而我们要做的就是谈谈如何选择这两个参数值θ0和θ1，选择不同的参数θ0和θ1，我们会得到不同的h函数，也就是不同的假设函数，例如对于下面几种情况，对于不同θ0和θ1，其图像时不一样的：

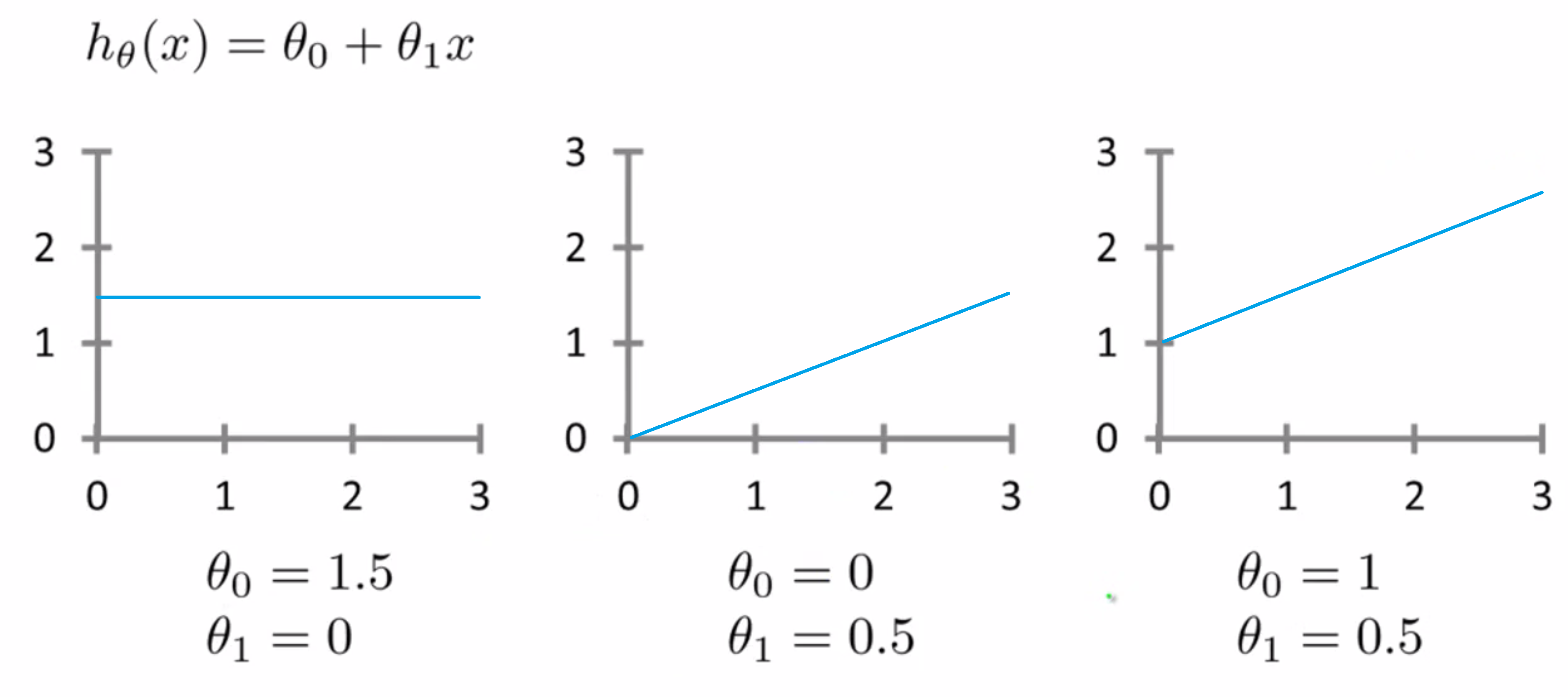
而现在假如我们有一个训练集如下，我们要做的就是，得出θ0 θ1这两个参数的值，来让假设函数（h函数）表示的直线 尽量地与这些数据点很好的拟合：

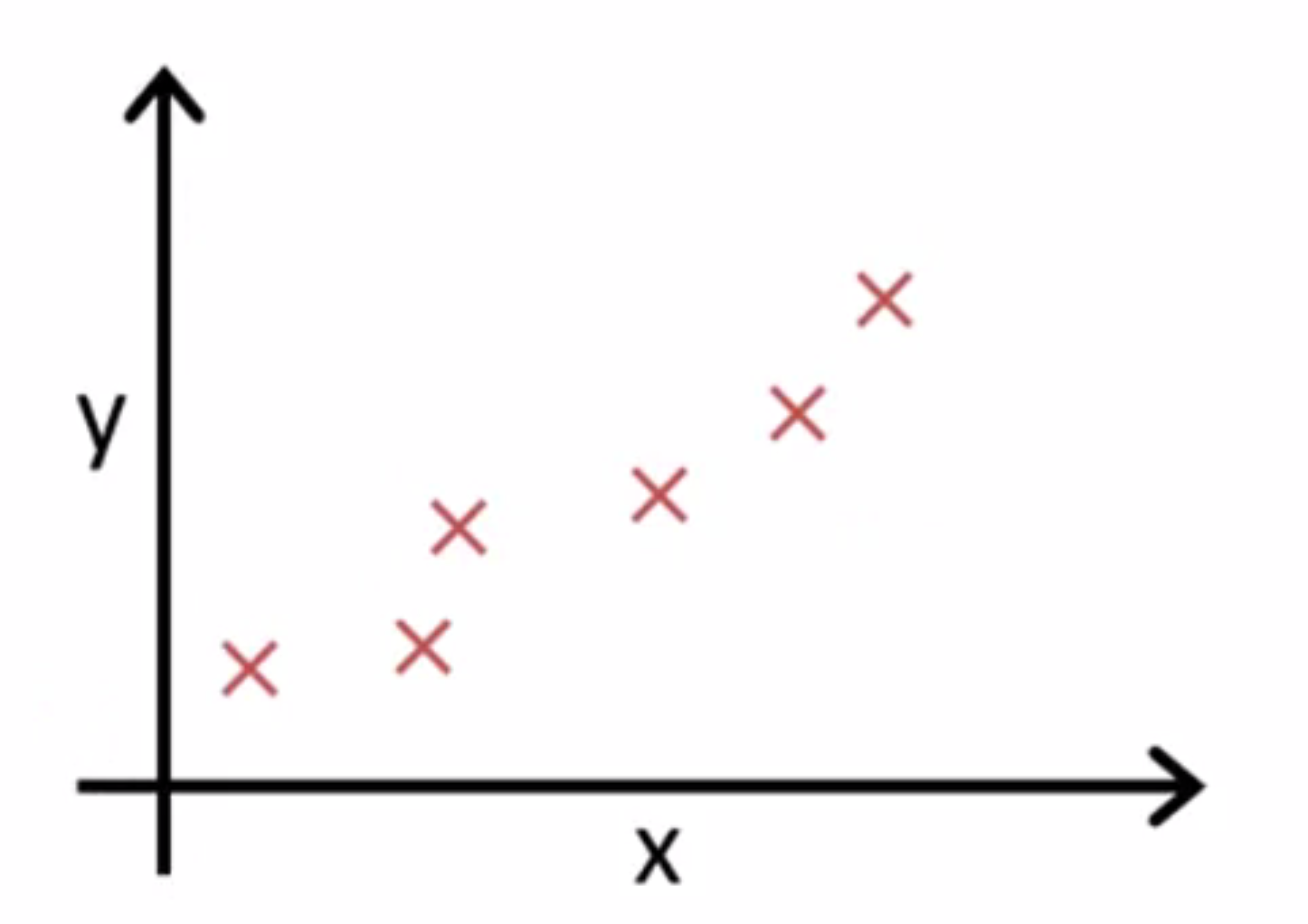
也许就像下面的的这条线一样:

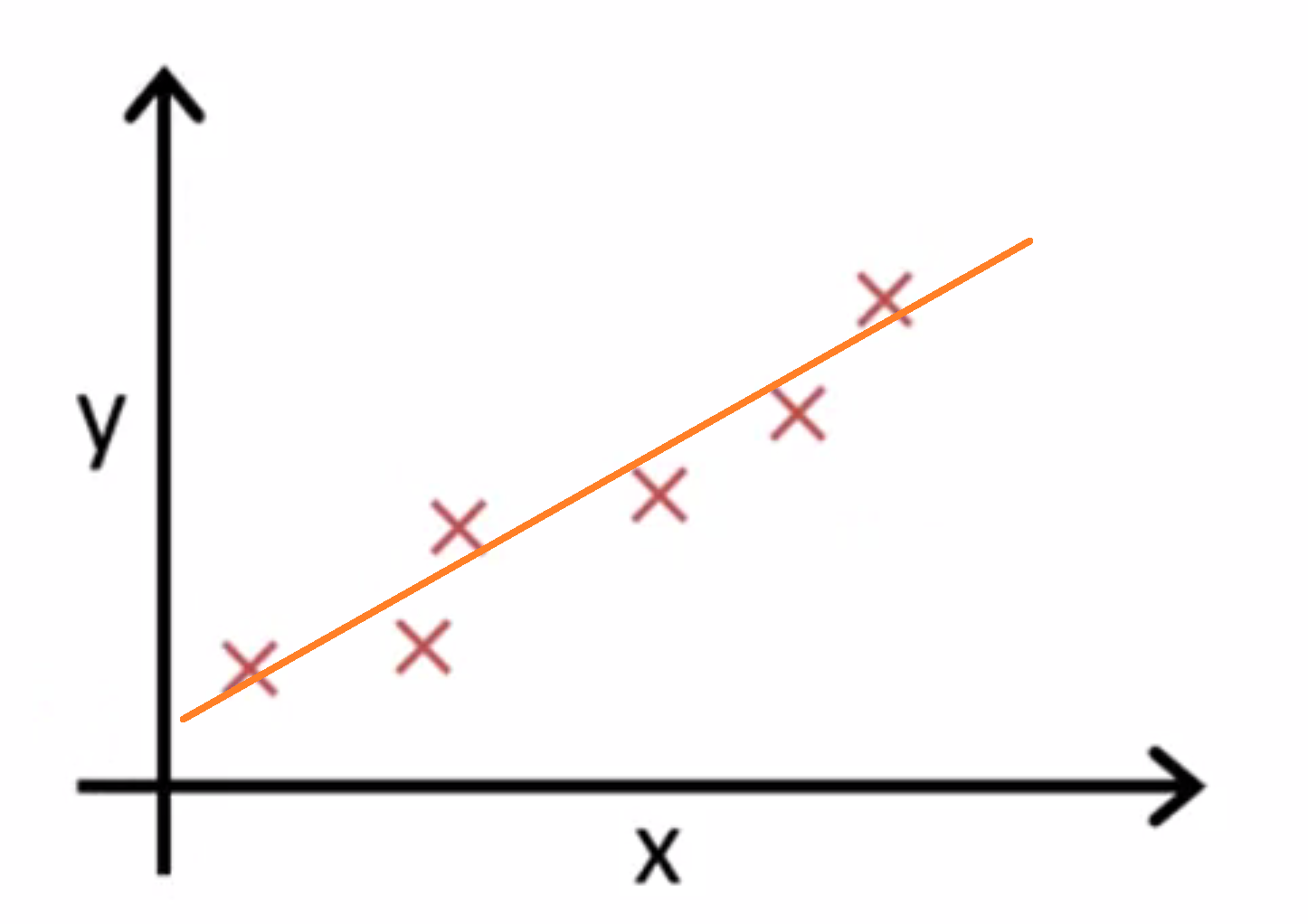
那么我们如何得出θ0和θ1的值，来使它很好地拟合数据的呢？我们的想法是，我们要选择参数θ0 θ1使h(x)，也就是输入x时我们预测的值最接近该样本对应的y值。所以对于我们的训练集，我们要尽量选择合适的参数值，使得在训练集中给出的x值，我们能合理准确地预测y的值。

让我们给出给出标准的定义：在线性回归中，我们要解决的是一个最小化问题，对于单个样本点，我们可以设出关于hθ（x）和y的差异函数G（hθ（x），y），通过选取θ0 θ1使得：minimize G（hθ（x），y）。

我们设法把这个式子展开，我想要h(x)和y之间的距离要小，所以我们要做的事情是尽量减少假设的输出与房子真实价格之间的差的平方，即G其实是一个平方函数，即minimize （hθ(x) - y）^2.

接下来我们考虑全体样本点，别忘了，我们用符号( x(i),y(i) )代表第i个样本，所以我想要做的是对所有训练样本的误差进行一个求和（对i=1到i=m的样本），即 minimize ∑（hθ(x) - y）^2。这时我们应该注意到，我们实际上考虑的是样本的平均误差，不然样本越大误差越大就可能导致错误。 所以我们要求的实际上时也就是minimize （∑（hθ(x) - y）^2 / m），而在实际运用中，为了方便，我们通常对求和值的二分之一求最小值，即求minimize （∑（hθ(x) - y）^2 / 2m）。这个最小值所对应的θ0值和θ1值就是我们所求的。我们知道hθ(x)=θ0+θ1*x，这意味着我们要找到θ0和θ1的值来使这个表达式的值最小，即这个表达式因θ0和θ1的变化而变化。

因此简单地说，我们正在把这个问题变成找到能使我的训练集中预测值和真实值的差的平方的和的1/2m倍最小的θ0和θ1的值。因此这将是我的线性回归的整体目标函数，为了使它更明确一点，我们可以改写这个函数，我们可以定义一个代价函数 J(θ0,θ1) = minimize （∑（hθ(x) - y）^2 ） / 2m 。我们想要做的就是关于θ0和θ1 对函数J(θ0,θ1)求最小值所对应的θ0,θ1，这就是我们所谓的代价函数。代价函数也被称作平方误差函数，有时也被称为平方误差代价函数。

事实上我们之所以要求出误差的平方和，是因为误差平方代价函数，对于大多数问题，特别是回归问题是一个比较合理的选择。当然还有其他的代价函数也能很好地发挥作用，但是平方误差代价函数可能是解决回归问题最常用也是最简单的手段了，在后续的BLOG中 我们还会谈论其他的代价函数。

代价函数直观感受

只考虑θ1的简化情况

在上面，我们给了代价函数一个数学上的定义，现在我们通过一些例子来获取一些关于代价函数的直观感受。首先让我们看看代价函数到底是在干什么，我们之前学习了几个重要的概念：

我们想找一条直线来拟合我们的数据集，所以我们用 θ0 θ1 等参数来得到这个假设函数h，而且通过选择不同的参数，我们会得到不同的直线拟合；然后我们还提到了一个代价函数，这就是我们的优化目标，即我们的目标是求出代价函数最小时对应的θ0和θ1。

为了更加直观地感受代价函数，我们先使用一个简化的假设函数hθ（x）= θ1*x， 我们可以将这个函数看成是把 θ0 设为0的一个假设函数，所以相当于我们只有一个参数θ1，所以我们的优化目标是将 J(θ1) 最小化。

用图形来表示就是当θ0 等于零时，就意味这我们选择的假设函数会经过原点也就是经过坐标 (0,0)，也就是一个正比例函数。我们要理解的是这两个重要的函数，第一个是假设函数h，第二个是代价函数J。注意这个假设函数 h(x) 对于一个固定的 θ1 这是一个关于 x 的函数，所以这个假设函数就是一个关于 x 的函数；与此不同的是，代价函数 J 是一个关于参数 θ1 的函数，而 θ1 控制着假设函数对应的直线的斜率：

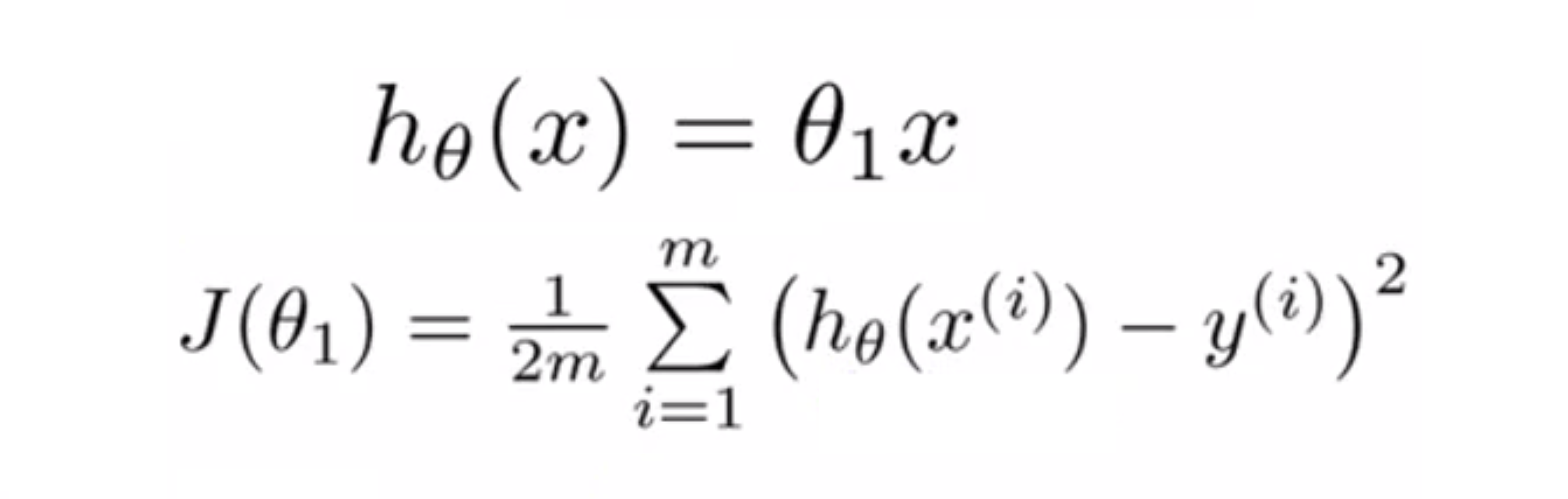
现在我们假设我们的训练样本包含了三个点 (1,1) (2,2) 和 (3,3)，让我们来看看hθ（x） 和 J（θ1）：

现在我们选择一个值 θ1，当 θ1 = 1 时看起来就会像是下面这条直线，且计算出此时J(θ1) = 0，所以我们现在知道了 J(1) 是0，让我们把这个画出来：

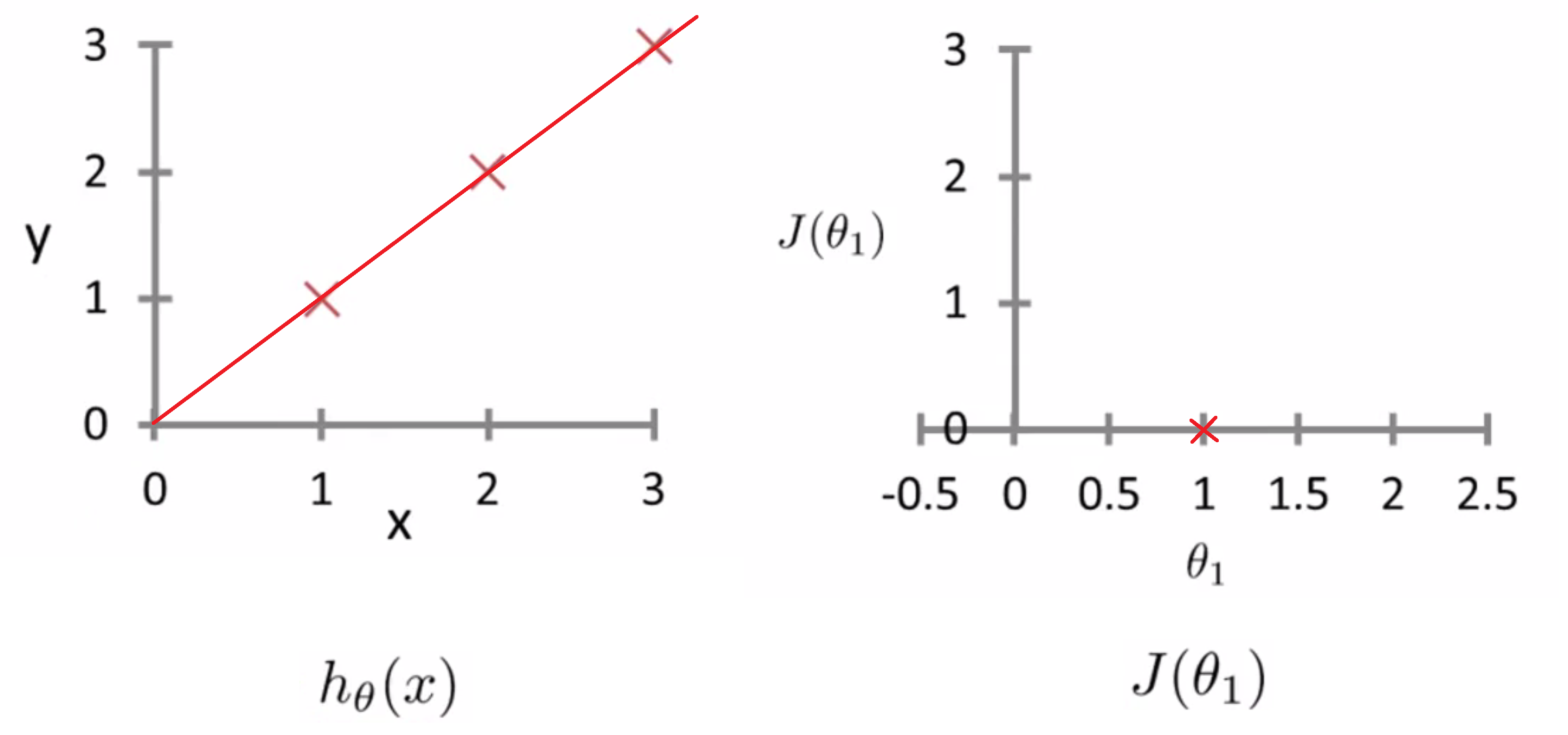
让我们继续把函数画出来，现在我们来看其它一些样本，θ1 可以被设定为任意取值，所以我们看看如果 θ1 等于0.5会发生什么呢？继续把它画出来，在这个条件下，我们的假设函数看起来就是下面这样，这条线的斜率等于0.5，且计算出此时J(0.5) = 0.58，所以我们继续把点画出来：

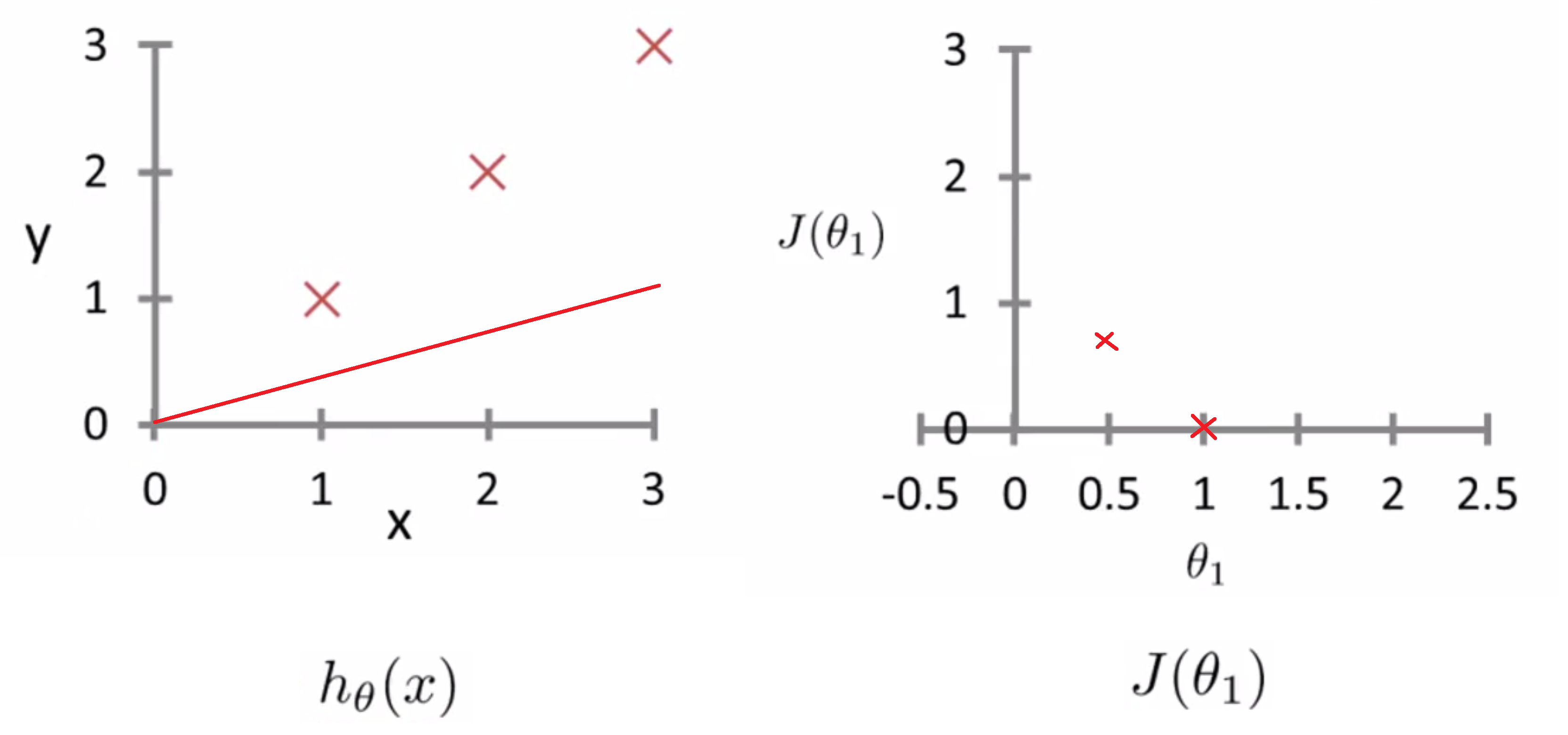
通过不断地计算不同θ1对应的J值，你可以慢慢地得到这条曲线，这就是 J(θ) 的样子了：

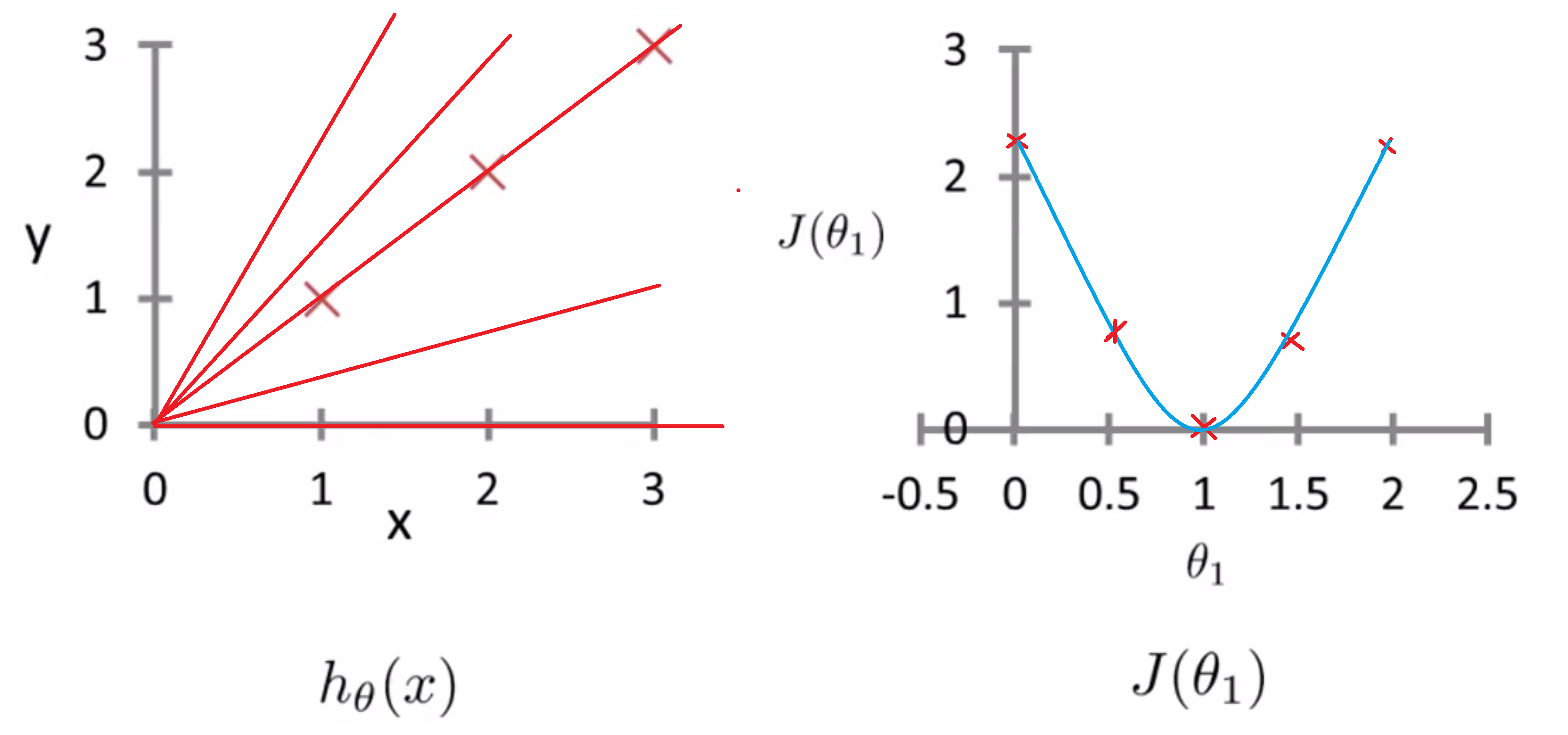
还记得我们学习算法的优化目标吗？我们想找到一个 θ1 的值来将 J(θ1) 最小化，对吧。我们来看这条曲线，让J(θ1) 最小化的值是 θ1 等于1，然后你看此时的θ1确实就对应着最佳的通过了数据点的拟合直线，这条直线就是由 θ1=1 的设定而得到的，然后对于这个特定的训练样本，我们最后能够完美地拟合，这就是为什么最小化 J(θ1) 对应着寻找一个最佳拟合直线的目标。

总结一下，在这一部分，我们看到了具体的图像来理解代价函数，而为了直观地做到这个，我们简化了算法，让这个函数只有一个参数 θ1 也就是说我们把 θ0 设定为0，在下一部分里，我们将回到原来的问题的公式，并且看一些带有 θ0 和 θ1 的图形，也就是说我们不把 θ0 设置为0了，希望这会让你更好地理解在原来的线性回归公式里，代价函数 J 的意义。

考虑上θ0

我们在上一块中，直观地感受了只考虑θ1时假设函数和代价函数的关系，我们这次加上θ0。我们考虑如下房价数据组成的训练集数据：

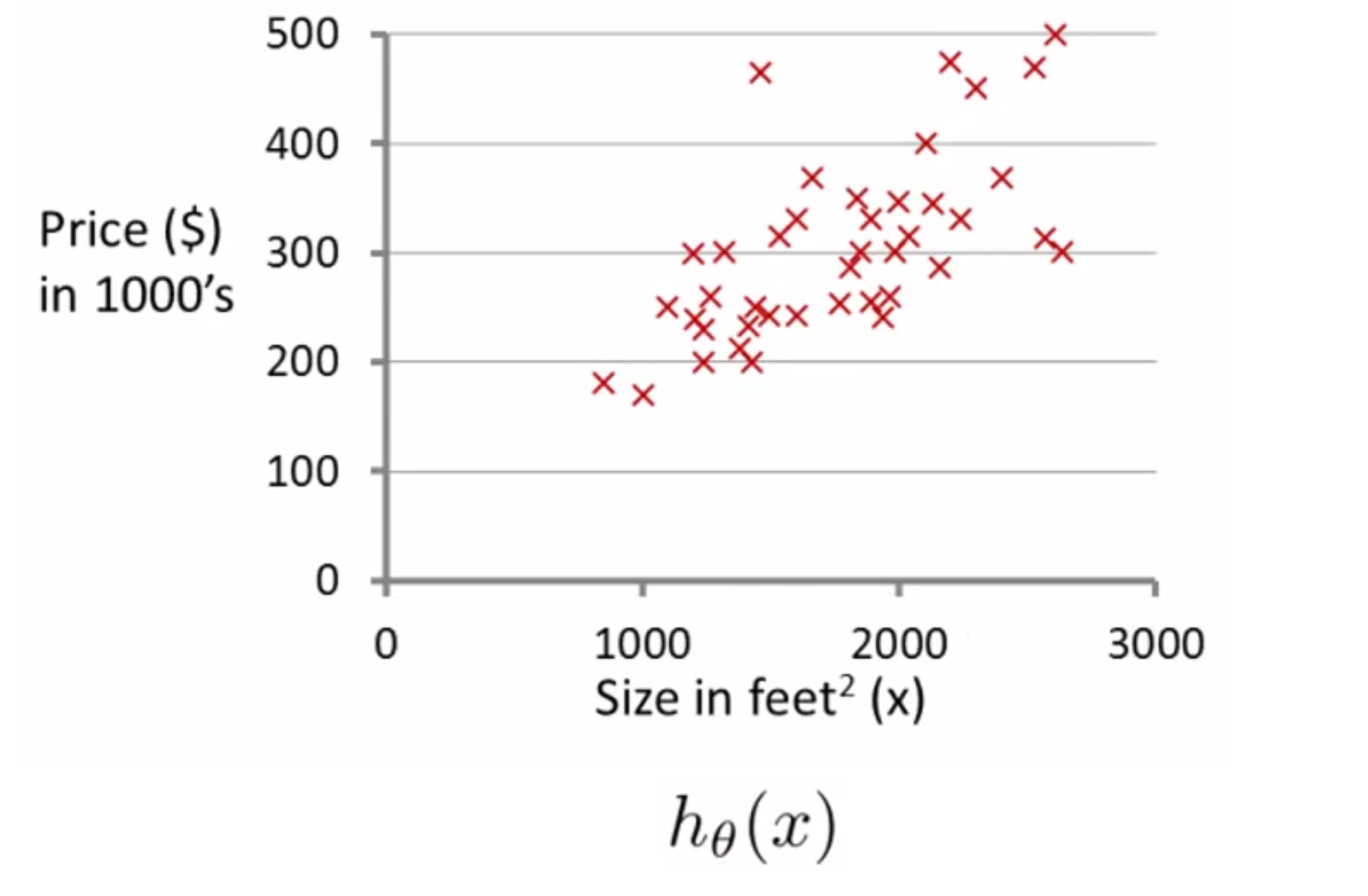
让我们来构建某种假设函数，就像下面条线一样，很显然这不是一个很好的假设，但不管怎样，如果我假设θ0等于50 而θ1等于0.06的话，那么我将得到这样一个假设函数，对应于下面这条直线：

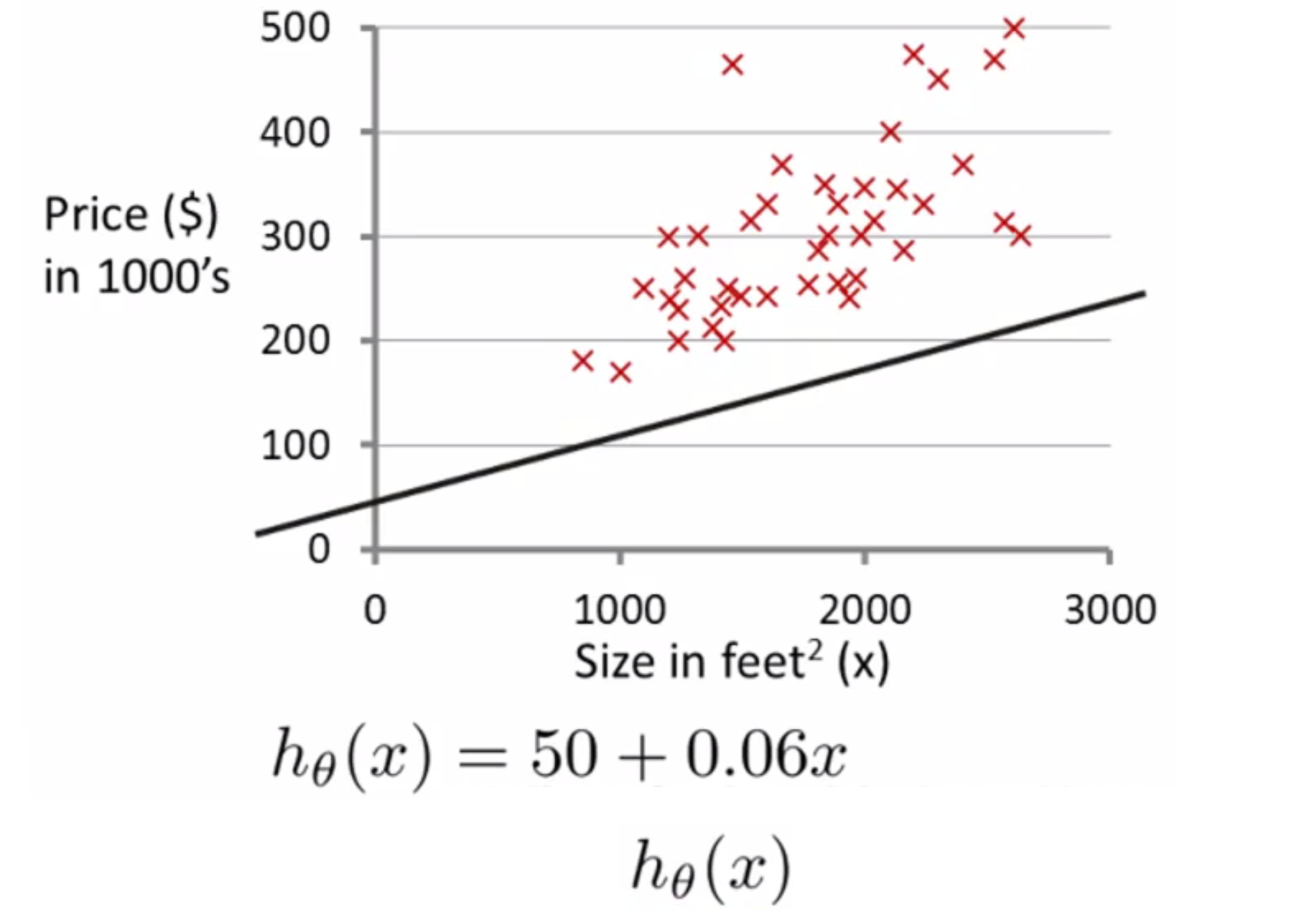
给出θ0和θ1的值，我们画出代价函数的图像，上一次我们是只有一个θ1，也就是说，画出的代价函数是只关于θ1的函数，故图像是二维的；但现在我们有两个参数θ0和θ1因此图像就会复杂一些，变成三维的了。当只有一个参数θ1的时候 我们画出来是一个弓形函数，而现在我们有了两个参数，但代价函数仍然呈现类似的某种弓形，实际上其呈现形状取决于训练样本。你可能会得到这样的图形：

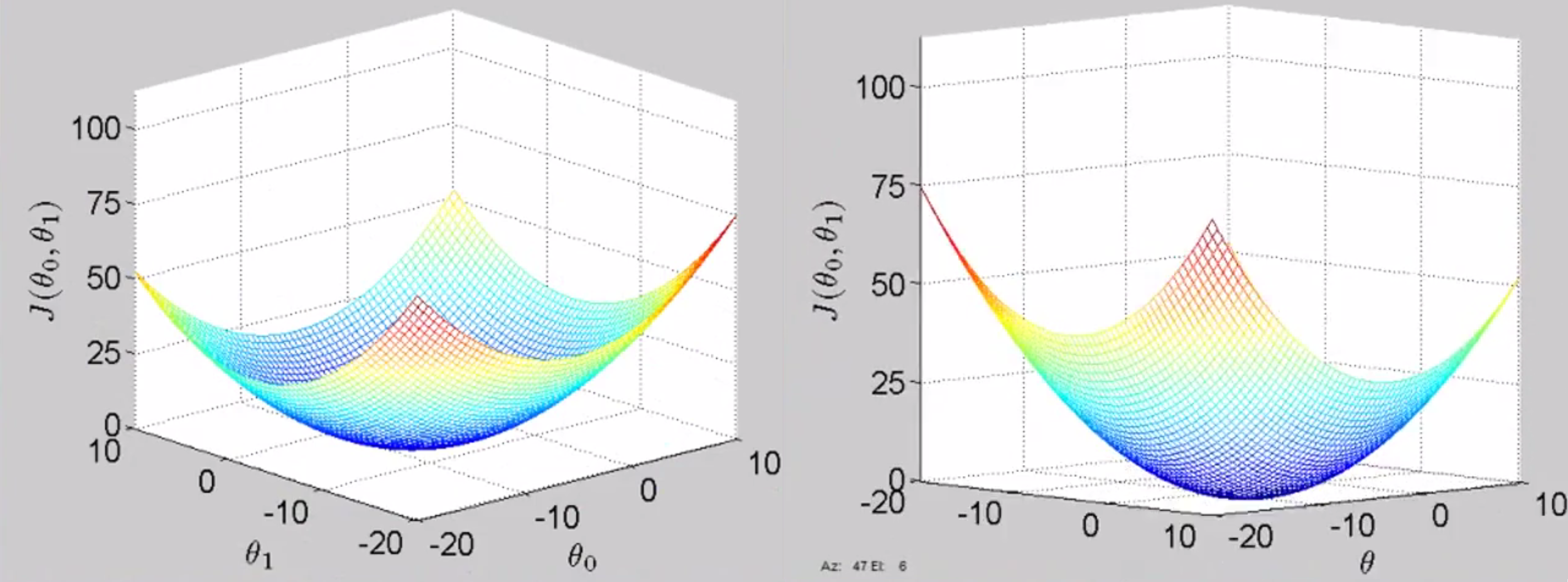
因此这是一个三维曲面图，两个轴分别表示θ0和θ1，随着你改变θ0和θ1的大小，你便会得到不同的代价函数J(θ0,θ1)。对于某个特定的点 (θ0,θ1) 这个曲面的高度 也就是竖直方向的高度，就表示代价函数 J(θ0,θ1) 的值。但这样观察还是有些不太方便，所以为了描述方便，我们经常用轮廓图来表示。下边就是一个轮廓图，两个轴分别表示 θ0 和 θ1 而这些一圈一圈的椭圆形，每一个圈就表示 J(θ0,θ1) 相同的所有点的集合，有点类似于等高线图：

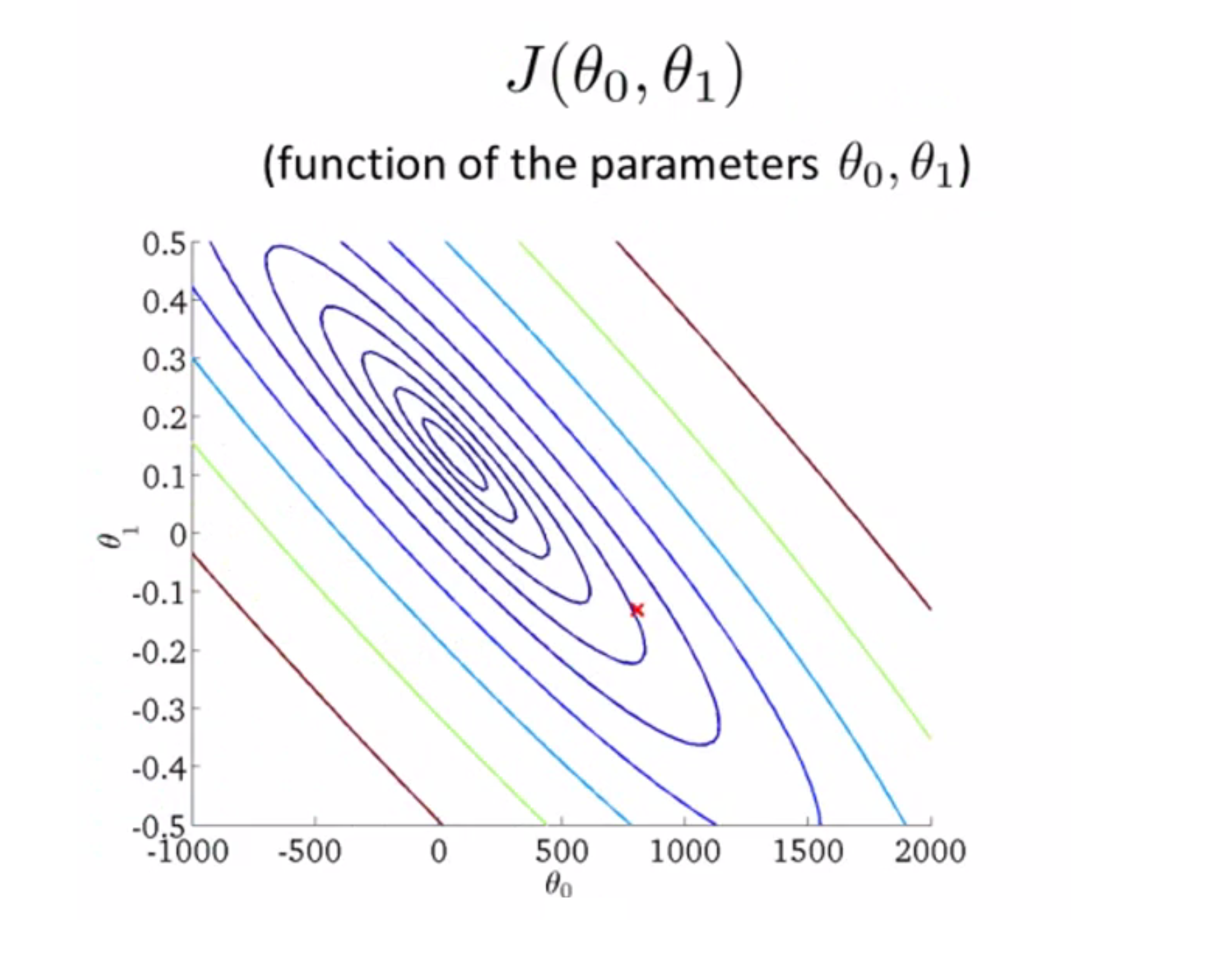
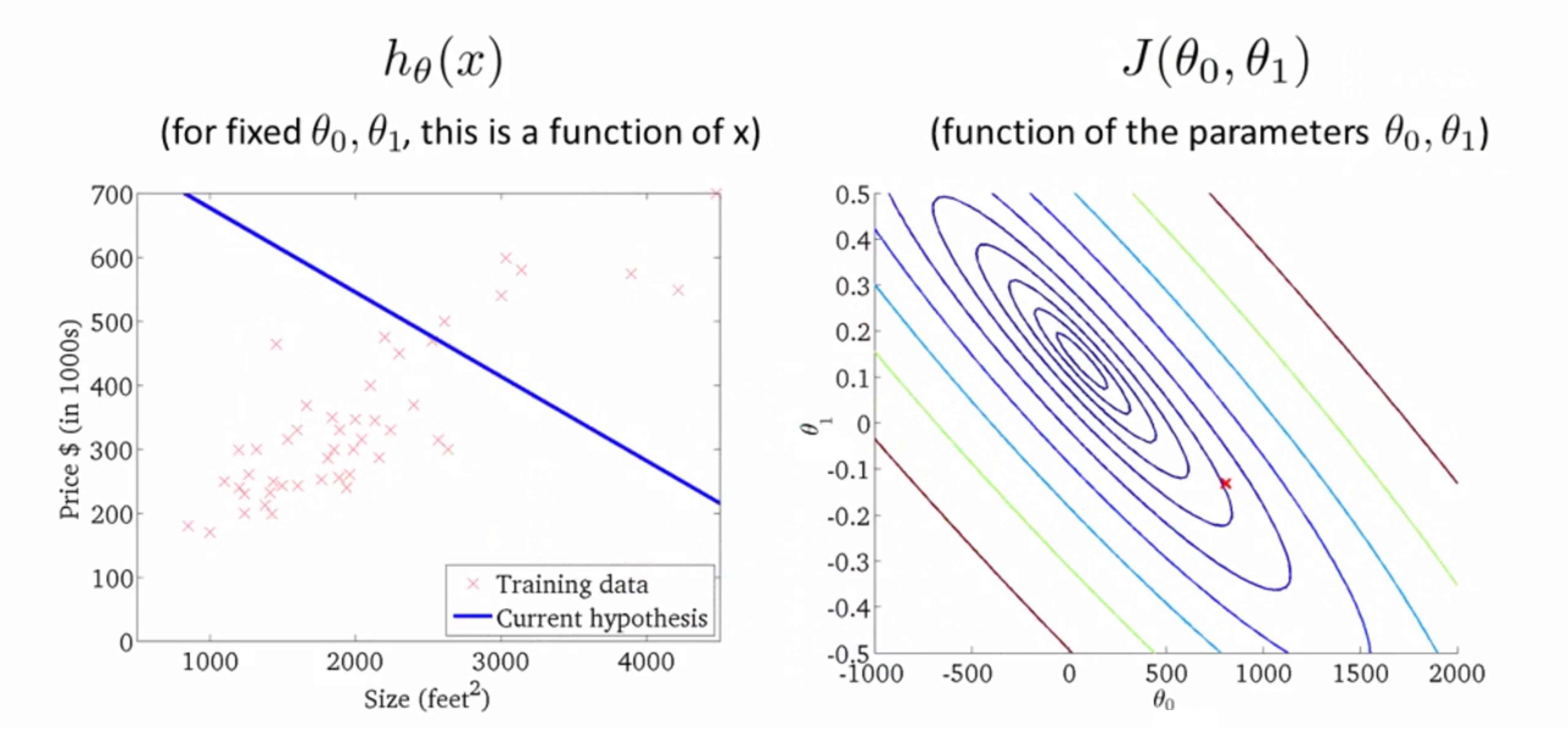
接下来让我们看几个例子：如下图轮廓图中有一点红色叉叉，这个点表示θ0等于800，θ1等于-0.15的情况，而这个点也对应于左边这样一条线，当然这条线并不能很好地拟合数据，并且你也发现了这个代价值，就是这里的这个红色叉叉代表的值，距离最小值点还很远，也就是说这个代价值还是算比较大的，因此不能很好拟合数据：

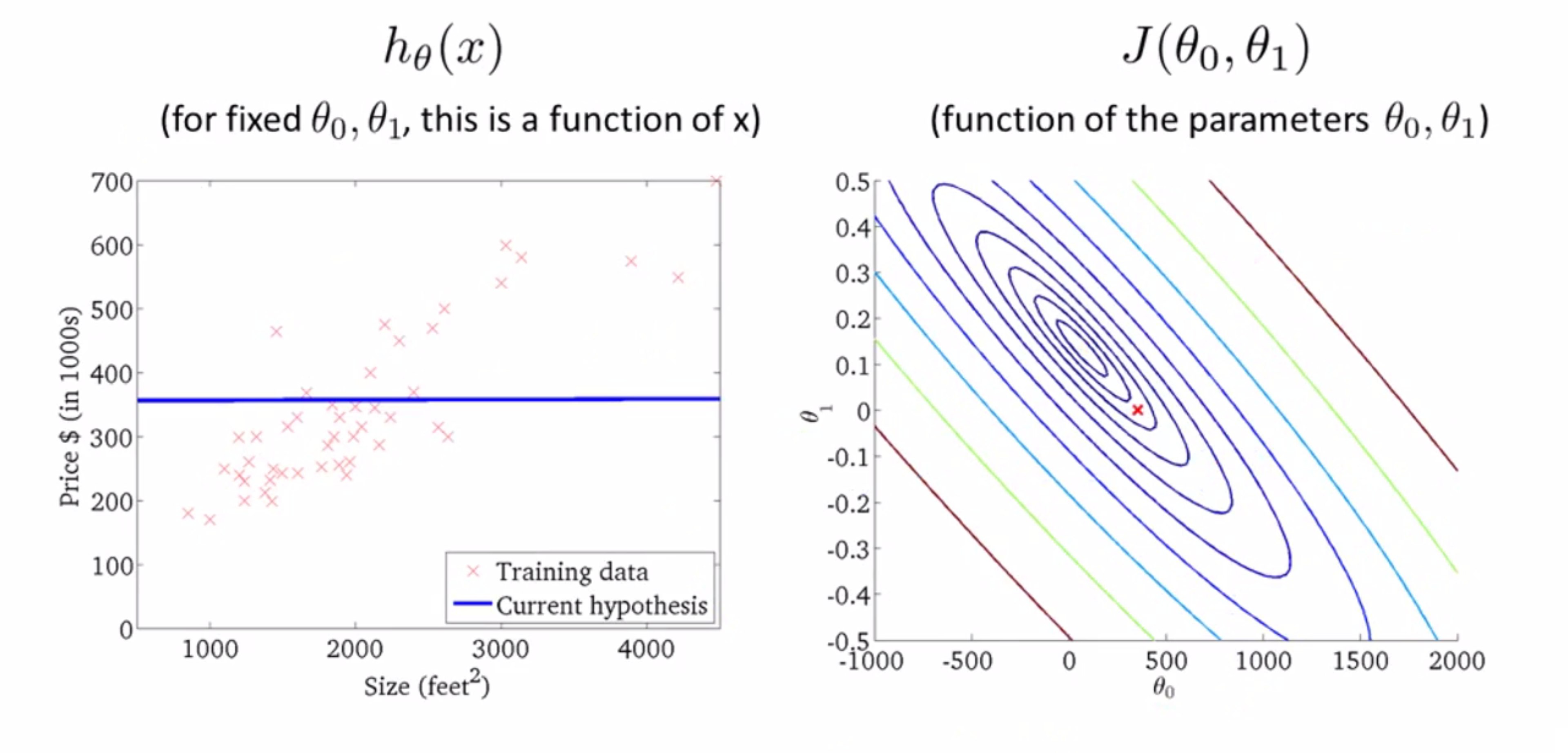
下面另一个假设，你不难发现，这依然不是一个好的拟合，但比刚才稍微好一点。这里 θ0 的值为360而θ1 的值为0，也就是h(x) = 360 + 0 × x，这就是假设函数。这个假设同样也有某个代价值，而这个代价值就对应于这个代价函数在这一点红色叉叉对应的的高度：

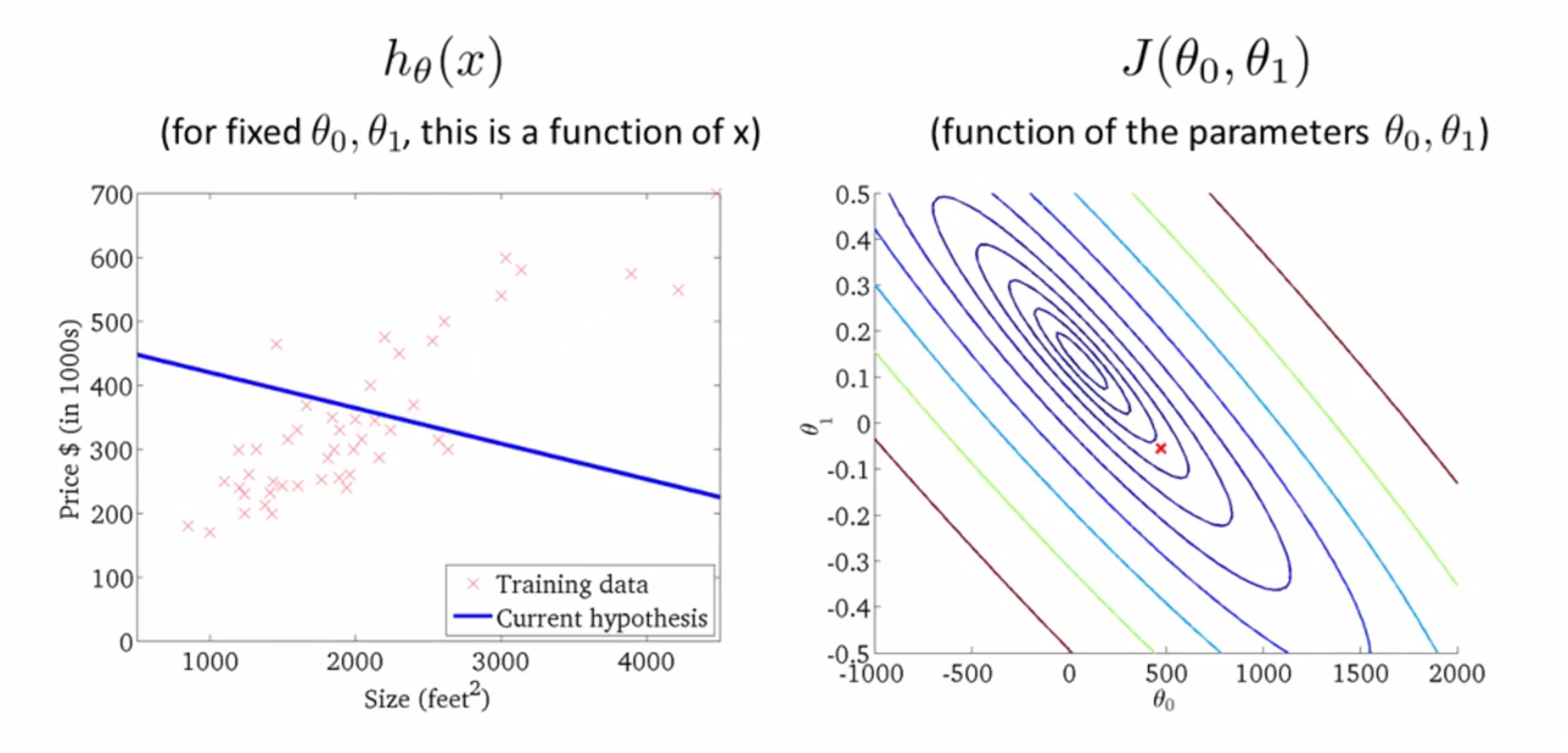
下面另一个例子，这个点这组 θ0 和 θ1 也对应着一条直线。假设函数h(x) 同样地还是对数据拟合不好，慎重离最小值更远了：

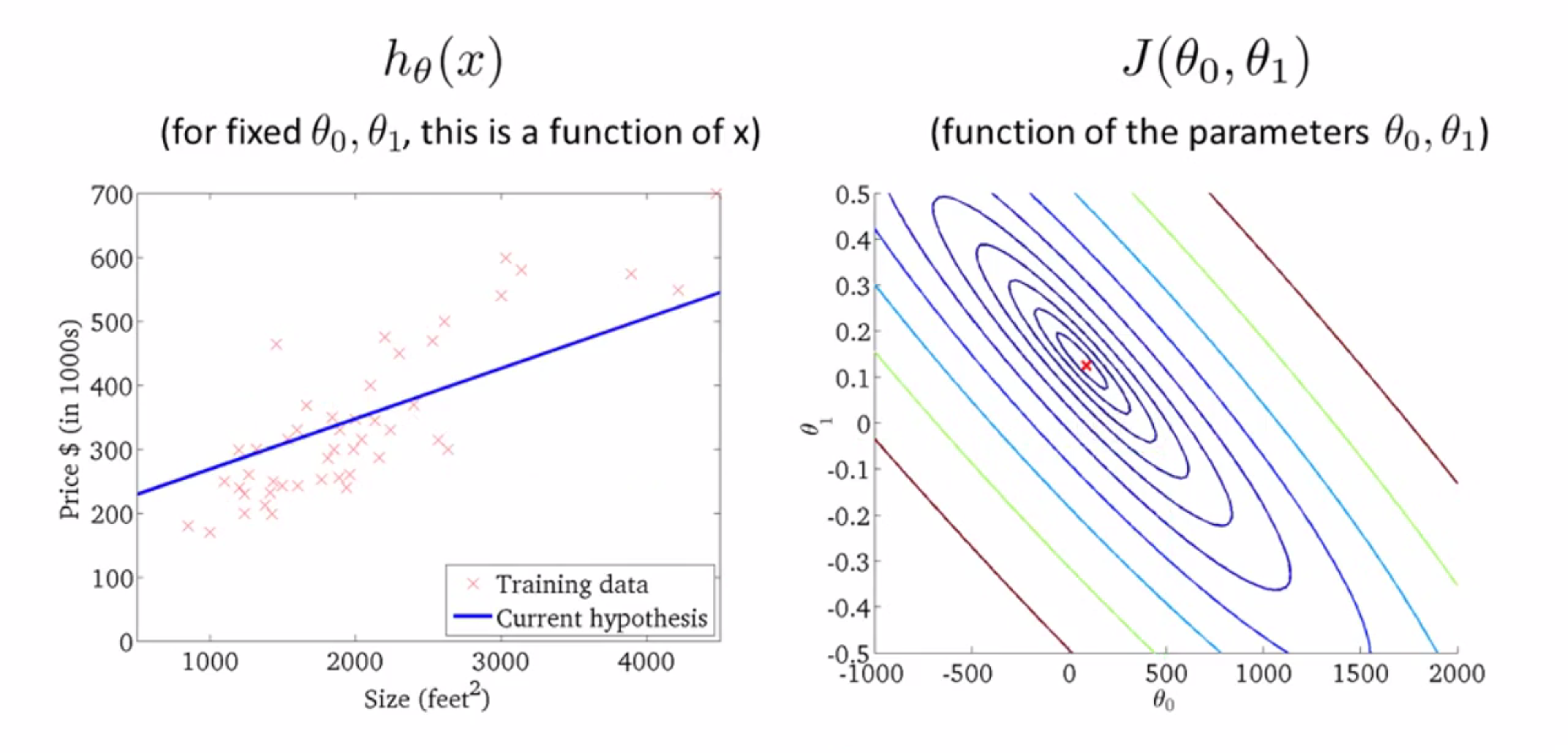
我们再看最后一个例子，你看轮廓图里的红色叉叉，这个点其实不是最小值，但已经非常靠近最小值点了，所以这个点对数据的拟合就很不错：

当然，这只是让我们直观地理解代价函数和函数拟合度之间的关系，我们真正需要的是一种有效的算法能够自动地找出这些使代价函数J取最小值的参数θ0和θ1来。我想我们也不希望编个程序把这些点画出来，然后人工的方法来读出这些点的数值，这很明显不是一个非常好的办法。事实上，我们之后就会一同遇到更复杂、更高维度、更多参数的情况，因此更无法将其可视化，因此我们真正需要的是编写程序来找出这些最小化代价函数的θ0和θ1的值。之后我们将一起学习一种算法，一种能够自动地找出能使代价函数 J 最小化的参数θ0和θ1的值的算法来解决这个问题。

结语

通过这篇BLOG，我们一同了解了线性回归模型和代价函数，之后，我们还会一同学习一种最小化代价函数的算法来解决我们的线性回归模型问题。希望你能有所收获。最后希望你喜欢这篇BLOG！