最近刚刚打完ACM的校队选拔赛,最后幸运女神眷顾,压线进了校队[做梦笑醒的说]。在这段时间的集训中,新学习了很多很有意思的算法,今天就让我们一起来学习回文串题目的大杀器——回文树吧!
思考一下
现在我们提出一个问题:
假如给你一个长度为 n 的字符串 S (n≤1e5),需要你求解本质不同的回文串的数量及各自的出现次数是多少(不包括空串)。[本质不同的字符串通俗来说就是长的不一样的字符串]
是不是看到题目就开始蒙了?关于回文串的算法,我们先前只学习过Manacher(还不会的同学或者不了解回文串的同学可以点击这里!)但是可惜的是,Manacher只能求解最长的回文串长度,无法求解本质不同的回文串的个数和其出现次数。那就考虑暴力算法?那肯定也是不太可行的,O(n^3)的算法复杂度带来的一定是TLE。
那么有没有一种算法能在O(n)的时间复杂度下统计本质不同的回文串的数量呢?当然是有的!回文树应时而生。
回文树的一些定义
什么你没听过回文树?那是很正常的。回文树是一种新兴的数据结构,由Mikhail Rubinchik在2015年发表,瓮文涛于2017年国家集训队论文详细介绍,下面我们先了解一下在本篇BLOG中一些名词的定义:
翻转
对于一个串 S1 S2 C3 …… Sn ,其翻转为 Sn Sn-1 Sn-2 …… S1 。
回文串
一个串S被称为回文串,当且仅当S的反转与S本身相同。
回文子串
设串S'为串S的子串,且S'是回文串,则S'为S的一个回文子串。
严格后缀
对于一个串 S1 S2 S3 …… Sn ,对任意i>1,Si Si+1 Si+2 …… Sn 称为原串的严格后缀。
最长回文后缀
对于一个长度小于自己的后缀(即严格后缀),如果它是回文串,并且不存在比它更长的回文后缀,那么它就是最长回文后缀。
拼接表示法
设有串t和字符c,tc表示在字符串t后接上字符c,ct表示在字符串t前接上字符c。
回文树的结构
回文树长什么样呢?首先回文树不是一棵树(那为什么叫回文树[别急慢慢往下看]),而是由两棵树构成的森林。我们设这两棵树的根分别为even和odd。和AC自动机,字典树之类的结构类似,回文树上的每个点代表的都是一个本质不同的回文串,除了根节点外,其余的树上的每一个节点都和主串S中的回文串一一对应。树上的每条边都对应着一个字符[类似于字典树]。
设树上有一点i,其对于的字符串为 S ,设fi为其父亲节点,其对于的字符串为 S',设字符 C 为i和fi连边上对应的字符,用拼接表示法表示的话,则 C S' C = S。我们举个例子吧,比如说,对于某个点代表的回文串"aba",假如它有条代表字符'c'的连边,那么,"aba"就会指向一个代表着"cabac"的回文串的点。
我们知道,回文串无非分为两种,一种长度是奇数,一种长度是偶数。而在回文树上走,我们肯定不是一次只在后面添加一个字符,而是像上述方法一样在前后各添加一个字符。所以我们不难得出一点,如果一个串可以变成另外一个回文串,那么它的长度一定加上了一个偶数,即奇偶性不变。所以在回文树上,为了区分这两种不同的回文串,我们开创了两棵树,一棵以odd为根节点的代表长度为奇数的回文串,另一棵以even为根节点代表长度为偶数的回文串。
特别的,对于根节点even,其代表的是长度为0的一个不存在的虚拟回文串;而对于odd,为了使其树上节点代表回文串的长度均为奇数,其代表的则是长度为-1的一个不存在的虚拟回文串,而odd的儿子对应的字符串为连出边对于的字符。
同样的,类似于AC自动机有fail,后缀自动机有parent,当失配的时候回文树也有fail向上跳,其指向的是该节点对应的字符串的最长回文后缀所对应的节点。特别的,定义odd和even的fail指针都指向odd。
那么fail指针有什么用呢?假如我们在字符串上匹配到 Sr 如果之前已经匹配出了一个回文Sl..Sr−1。那么,此时有两种情况,如果有Sl-1 = S就没有失配,继续匹配r+1就可以了。但如果失配了,因为r位置是不能变动的,所以我们能够挪动的只有l位置,设我们l移动到了l',而为了让Sl'-1..Sr是一个回文串,Sl'..Sr-1显然也要是一个回文串,而我们要找的回文串又要尽量长,所以l挪动到的位置l'就是Sl..Sr−1的最长回文后缀的开始位置。
那么回文树到底长啥样呢,让我们就设S=babbab从论文中的示意图一探究竟:
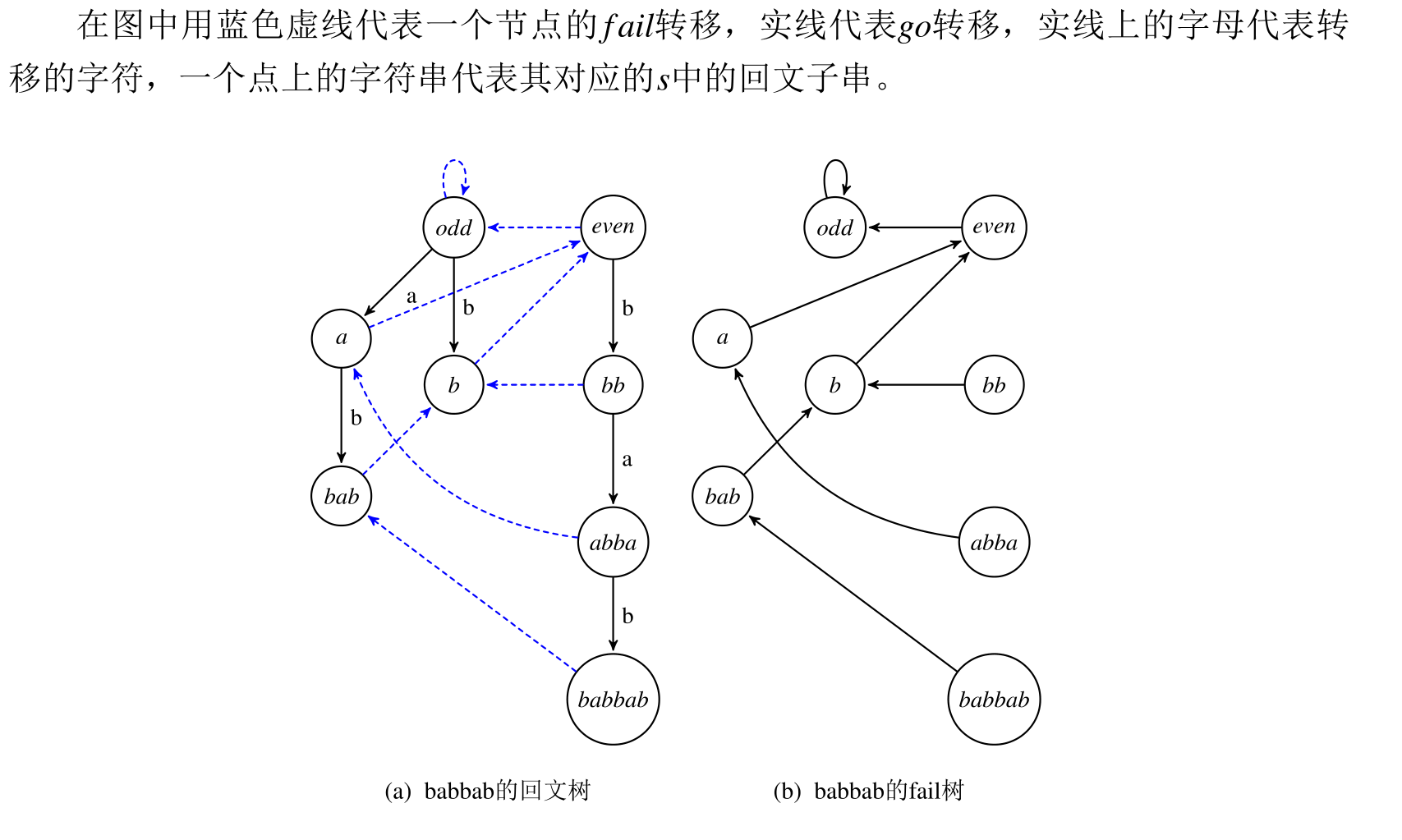
是不是很可爱呢?
回文树的一些结论
1.对于任何一个串S,它的本质不同的回文串的个数不会超过|S|个
2.如果在串S后面加入一个字符,新增的本质不同的回文串的个数不会超过1个
那么怎么证明的,我们可以使用数学归纳法,我们设|S|表示 串 S 的长度:
1.当|S|=1时,即当串S的长度为1时,显然成立。
2.如果我们知道|S|=x−1时成立,现在在S末尾插入x位置,其字符为c。如果以x位置结尾出现了两个新的本质不同的回文串,我们假设较长的从l1开始,较短的从l2开始
因为|Sl1 .. Sr|>|Sl2 .. Sr|,又根据回文串对称的性质,所以 Sl2 .. Sr 在Sl1 .. Sr 中的 Sl1 .. Sl1+(r-l2+1) 位置必定出现过,所以不存在两个本质不同的回文串,所以最多新增一个本质不同的回文串,所以到x位置出现的本质不同的回文串的个数最多为x个。
3.所以原命题为真。
同时,我们也证明了每次插入一个新的字符,最多增加一个本质不同的回文子串。
回文树的构造方法
看完了上面,应该都已经了解了回文树的一些基本要素,下面我们来着重介绍一下怎么构造回文树,并且会举出具体例子帮助大家学习。我们的构造采用增量法,也就是类似于后缀自动机的extend。
假设前面已经构造出了1..x−1的回文树,现在要加入第x个字符c,因为要接在x−1的后面,我们又知道最多一个产生一个新的本质不同的回文串。也就是我们需要在 S1 .. Sx−1 中,找到最长的某个回文后缀 Sl .. Sx−1 ,同时能够满足 Sl−1 = Sx ,因此我们只要只需要不停地寻找最长回文后缀,最长回文后缀的最长回文后缀,最长回文后缀的最长回文后缀的最长回文后缀……,直到满足条件。
根据回文树上的fail指针的含义,我们很容易知道知道,
只需要从上一个位置添加点的位置(也就是以x−1为结束位置的最长回文子串[程序中用last进行记录])所代表的节点开始,沿着fail一路上跳,检查是否满足 Sl−1 = Sx就行了。
假设这样找到的一个满足条件的位置p,设len[p]代表p点代表的回文串的长度,那么此时,Sx-len[p]-1 = Sx。不难证明这个位置p一定存在。(因为fail跳到最后是odd,其len值为-1,此时 Sx-(-1)-1 = S 恒成立)
在我们找到p后,如果p.son[c]也就是连边c已经存在,就证明这个回文串之前已经出现过了,那就什么都不用干,只需要在该字符串出现次数的计数器上加一,而因为这个回文子串已经存在过不需要重新建边。
否则,重新建一个点表示这个回文子串,假设点是n吧,然后p.son[c]=n,字符串出现次数的计数器设为1,现在我们要找n的fail啦,首先每次插入一个新的字符,最多增加一个本质不同的回文子串,所以fail指针指向的回文串一定是之前已经出现过的。再因为我们要找的是最长回文后缀,不能是自己,所以我们先令k=p.fail,然后就像前面一样的,再找到第一个满足 Slk−1 = Sn 的点,接着让k沿着代表 字符Sx 的边跳,然后n.fail=k,表示找到啦。
这样,我们的回文树就利用增量法构建出来啦。
我们下面就以S=babbab为例,一步步构造回文树吧:
首先加入b,S'=b,last=0,fail跳到odd结束,该字符串未出现过,新建节点2(b),fail指向odd:
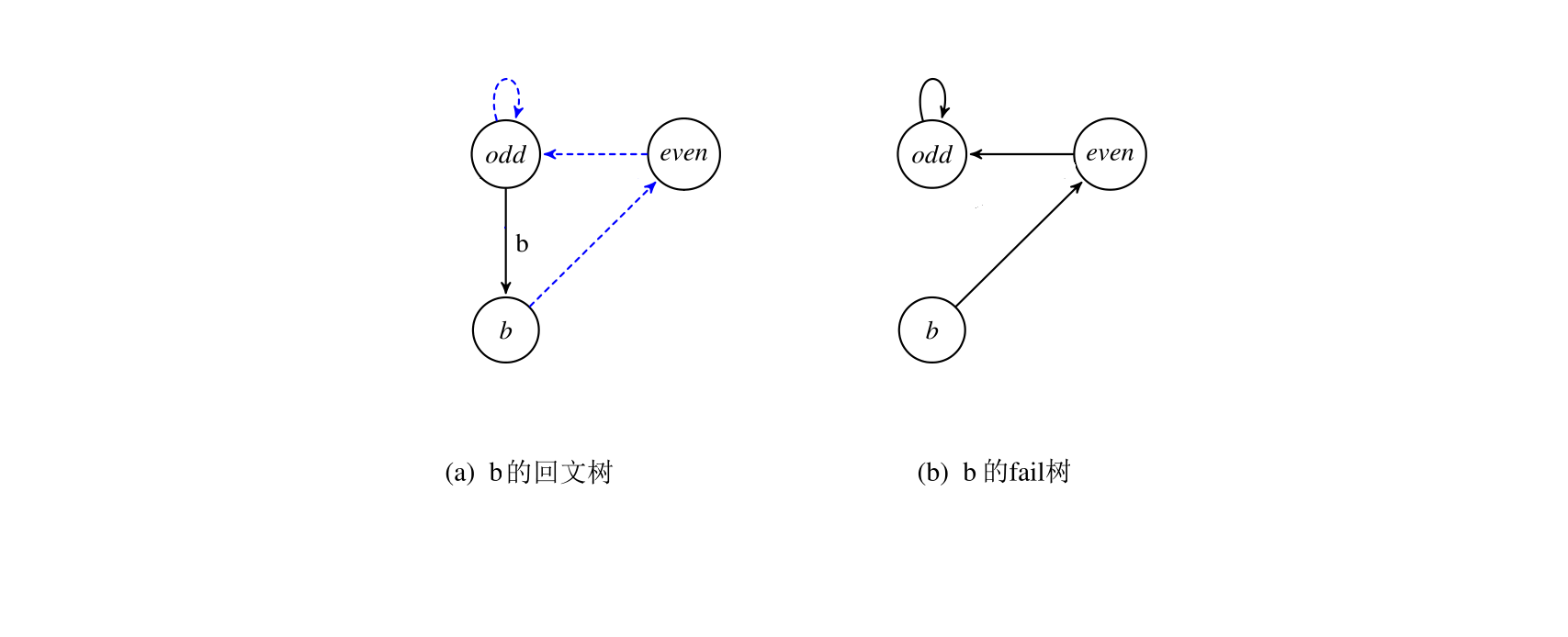
接着加入a,S'=ba,last=2,fail跳到odd结束,该字符串未出现过,新建节点3(a),fail指向odd:
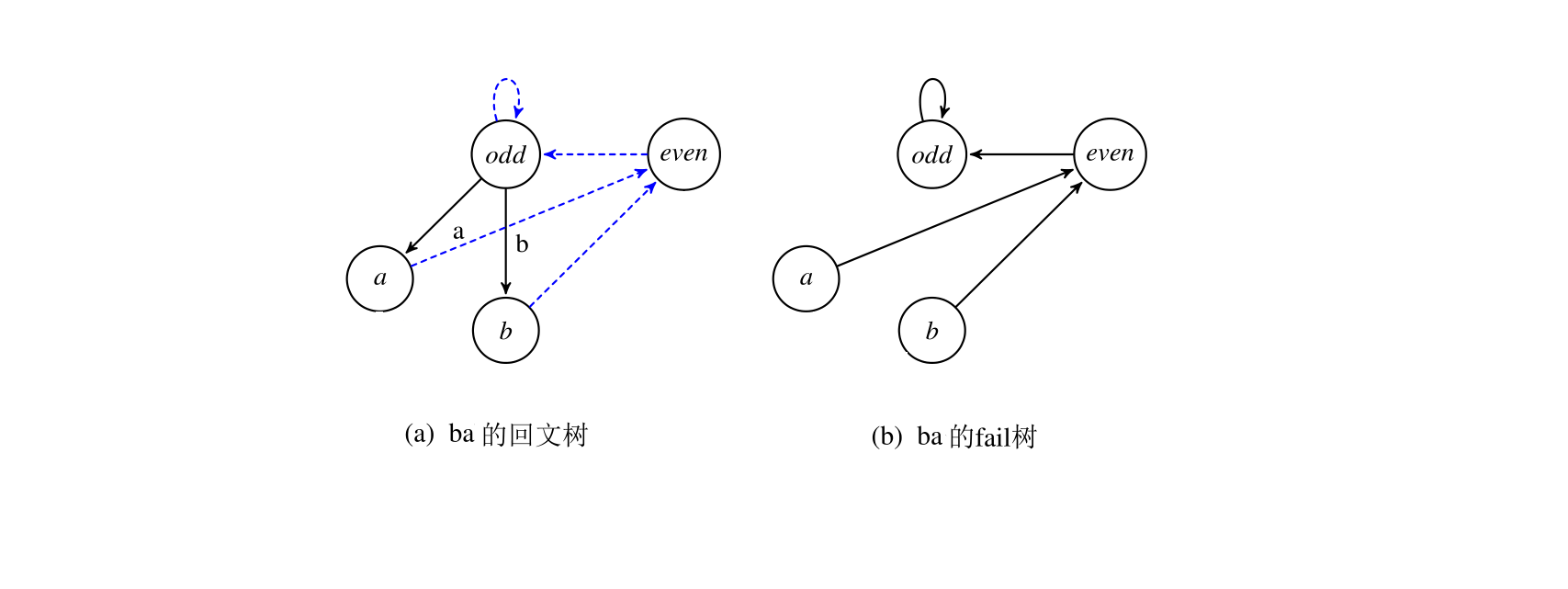
接着加入b,S'=bab,last=2,fail跳到3(a)结束,该字符串未出现过,新建节点4(bab),fail指向2(b):
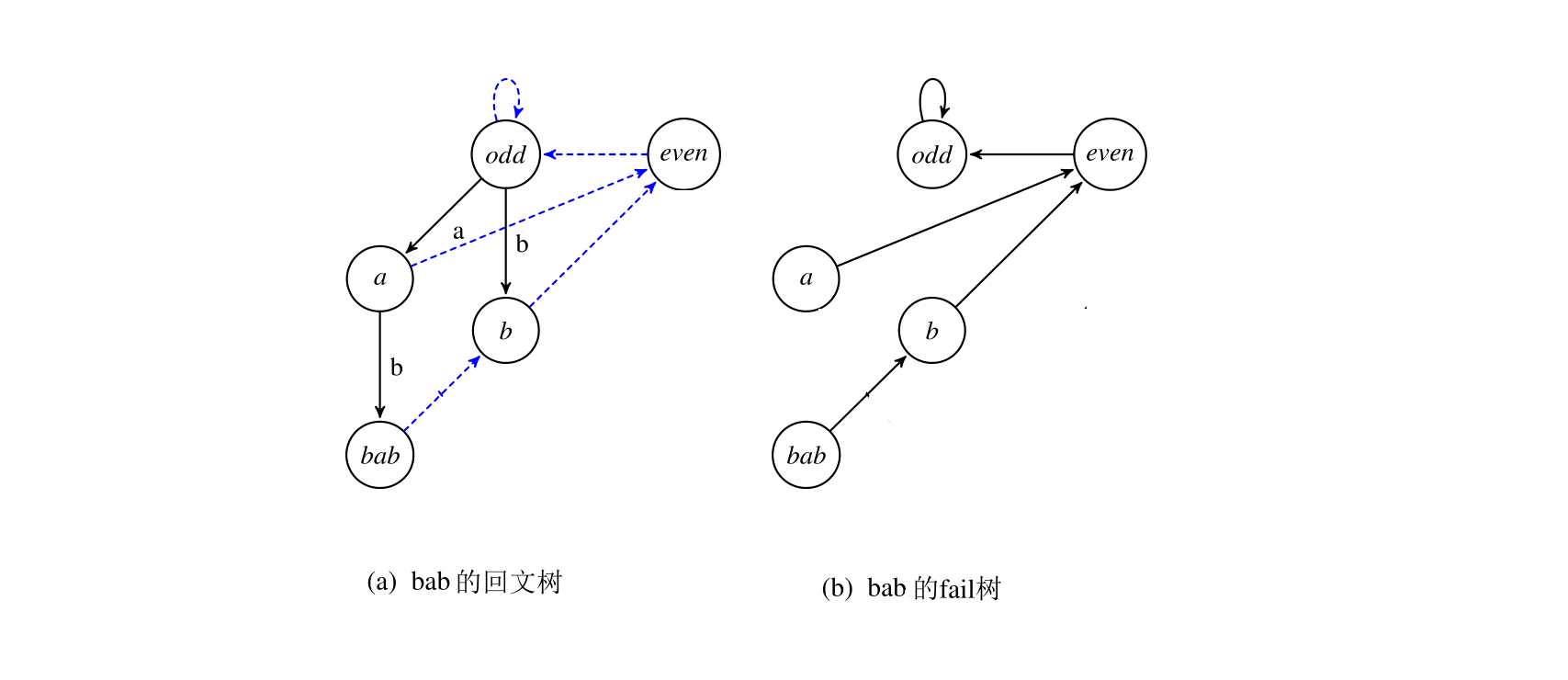
接着加入b,S'=babb,last=4,fail跳到even结束,该字符串未出现过,新建节点5(bb),fail指向2(b):
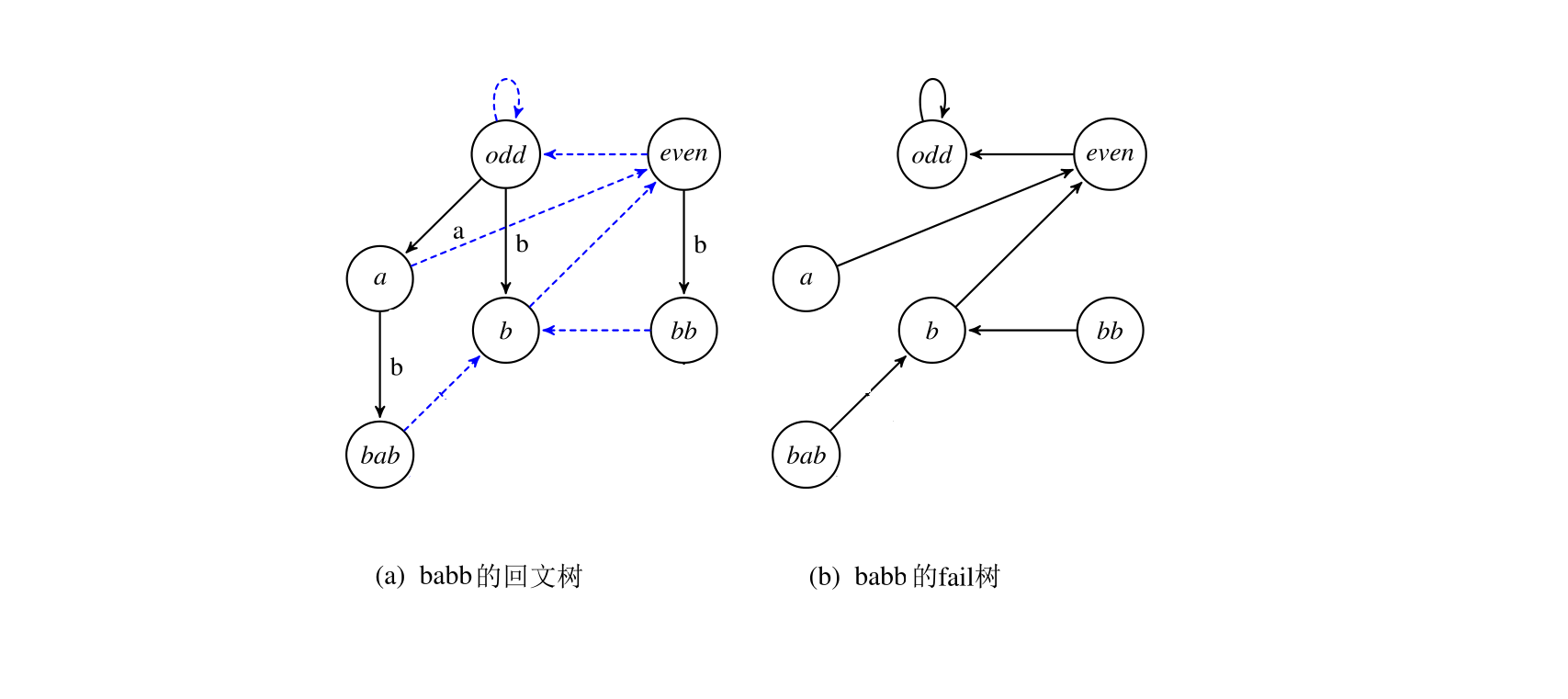
接着加入a,S'=babba,last=5,fail跳到5(bb)结束,该字符串未出现过,新建节点6(abba),fail指向3(bb):
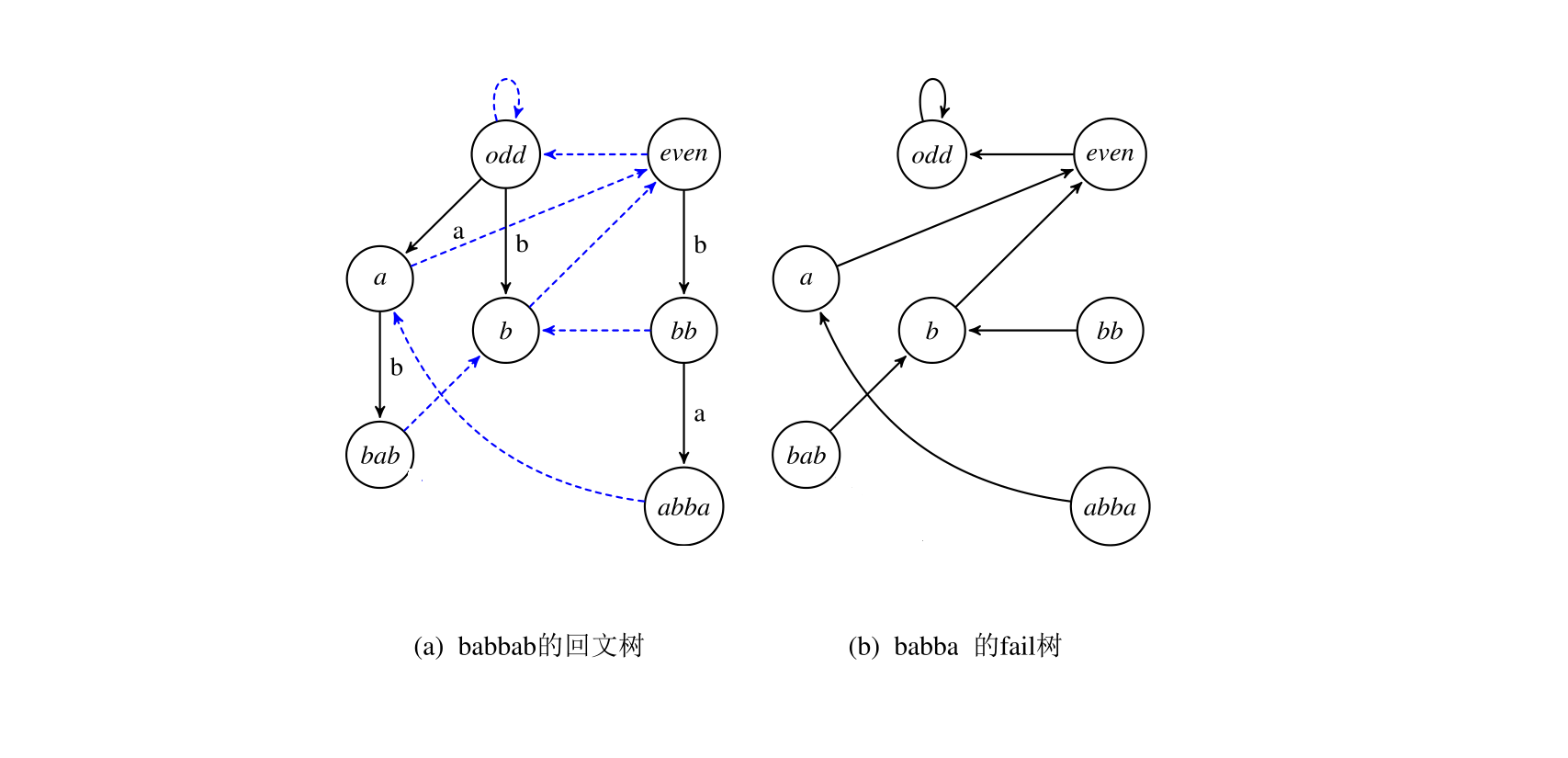
最后加入b,S'=babbab,last=6,fail跳到6(abba)结束,该字符串未出现过,新建节点7(babbab),fail指向4(bab):
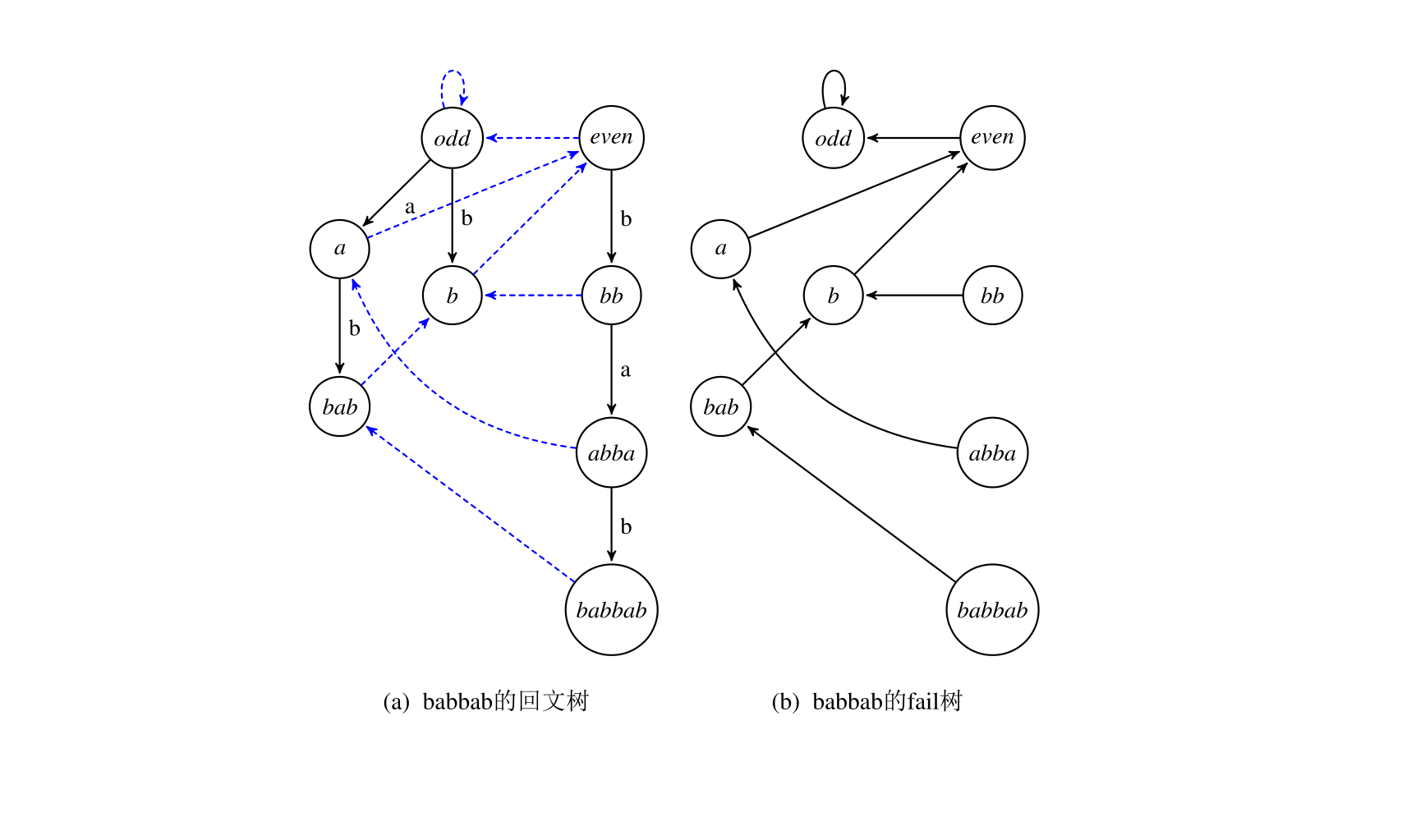
当然,正如上面所说odd和even两棵树的根节点的长度分别是−1和0,然后even的fail连向odd,odd的fail也连向自己。初始情况下的last=0,tot=1。(详见程序)
下面给出开头那个问题的模板:
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
char s[330000];//存储主串
int i,j,k,m,n,o,p,q,js,jl,tot,last;
//tot是树上总的节点数,last表示的是上一个回文串在树上的位置
int len[330000],fail[330000],cnt[330000],ch[330000][26];
//len[i]代表的是i号节点代表的回文串长度
//fail[i]代表的是i号节点的fail指针指向谁
//cnt[i]代表的是i号节点代表的回文串在主串中出现的次数
//ch[i]类似于字典树,维护回文树的儿子节点是谁
long long ans;
long long my_max(long long x,long long y)
//比较选取最大值
{
if(x>y)return(x);
else return(y);
}
int newnode(int x)
//新建一个长度为x的回文串的节点
{
tot++;
len[tot]=x;
return(tot);
}
int getfail(int x,int n)
///跳fail指针知道找到满足匹配条件的后缀回文为止
{
while(s[n-len[x]-1]!=s[n])x=fail[x];
return(x);
}
int main()
{
scanf("%s",s+1);//读入主串
s[0]=-1;fail[0]=1;last=0;
//初始化:偶数长度回文树的root的fail指向 数长度回文树的root
len[0]=0;len[1]=-1;tot=1;
//0号节点代表偶数长度回文树的root,初始化长度为0
//1号节点代表奇数长度回文树的root,初始化长度为1
int num=strlen(s+1);//获取字符串长度
for(int i=1;i<=num;i++)
{
s[i]-='a';
p=getfail(last,i);//获得满足条件的回文后缀p
if(ch[p][s[i]]==0)//如果有了转移就不用建了,否则要新建
{
q=newnode(len[p]+2);
//前后都加上新字符,所以新回文串长度要加2
fail[q]=ch[getfail(fail[p],i)][s[i]];
//因为fail指向的是原串的严格后缀,所以要从p的fail开始找起
ch[p][s[i]]=q;
//记录回文树
}
last=ch[p][s[i]];
//更新last
cnt[ch[p][s[i]]]++;
//该回文串在主串中出现次数加一
}
printf("%d\n",tot-1);//输出个数
for(int i=tot;i>1;i--)
{
cnt[fail[i]]+=cnt[i];
printf("%d ",cnt[i]);
}//输出次数
return 0;
} 回文树的经典例题
下面就让我们来看看经典例题吧!
[Luogu]P3649 [APIO2014]回文串
题目描述:
给你一个由小写拉丁字母组成的字符串 ss。我们定义 ss 的一个子串的存在值为这个子串在 ss 中出现的次数乘以这个子串的长度。对于给你的这个字符串 ss,求所有回文子串中的最大存在值。
输入格式:
一行,一个由小写拉丁字母(a~z)组成的非空字符串 ss。输出格式:
输出一个整数,表示所有回文子串中的最大存在值。输入输出样例
输入 #1
abacaba
输出 #1
7
输入 #2
www
输出 #2
4对于100%数据满足 1≤∣s∣≤300000。
模板题,用cnt记录一下每个串出现的次数即可。
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
char s[330000];//存储主串
int i,j,k,m,n,o,p,q,js,jl,tot,last;
//tot是树上总的节点数,last表示的是上一个回文串在树上的位置
int len[330000],fail[330000],cnt[330000],ch[330000][26];
//len[i]代表的是i号节点代表的回文串长度
//fail[i]代表的是i号节点的fail指针指向谁
//cnt[i]代表的是i号节点代表的回文串在主串中出现的次数
//ch[i]类似于字典树,维护回文树的儿子节点是谁
long long ans;
long long my_max(long long x,long long y)
//比较选取最大值
{
if(x>y)return(x);
else return(y);
}
int newnode(int x)
//新建一个长度为x的回文串的节点
{
tot++;
len[tot]=x;
return(tot);
}
int getfail(int x,int n)
///跳fail指针知道找到满足匹配条件的后缀回文为止
{
while(s[n-len[x]-1]!=s[n])x=fail[x];
return(x);
}
int main()
{
scanf("%s",s+1);//读入主串
s[0]=-1;fail[0]=1;last=0;
//初始化:偶数长度回文树的root的fail指向 数长度回文树的root
len[0]=0;len[1]=-1;tot=1;
//0号节点代表偶数长度回文树的root,初始化长度为0
//1号节点代表奇数长度回文树的root,初始化长度为1
int num=strlen(s+1);//获取字符串长度
for(int i=1;i<=num;i++)
{
s[i]-='a';
p=getfail(last,i);//获得满足条件的回文后缀p
if(ch[p][s[i]]==0)//如果有了转移就不用建了,否则要新建
{
q=newnode(len[p]+2);
//前后都加上新字符,所以新回文串长度要加2
fail[q]=ch[getfail(fail[p],i)][s[i]];
//因为fail指向的是原串的严格后缀,所以要从p的fail开始找起
ch[p][s[i]]=q;
//记录回文树
}
last=ch[p][s[i]];
//更新last
cnt[ch[p][s[i]]]++;
//该回文串在主串中出现次数加一
}
ans=0;
for(int i=tot;i>=1;i--)
{
cnt[fail[i]]+=cnt[i];
ans=my_max(ans,1ll*cnt[i]*len[i]);
}
printf("%lld\n",ans);//输出答案
return 0;
} 结语
通过这篇BLOG,相信大家对于回文串和回文树都有了一个全新的认识,接下来也会更新其他有意思的算法。最后希望你喜欢这篇BLOG!
蒟蒻你好帅,你要跟你生猴子
OrzOrzOrz
Orz您太强了
OrzOrzOrz
OrzOrzOrz
Orz