在上一篇BLOG中，我们介绍了二叉查找树的八种操作。但是有人会说，万一退化成链之类的不就超时了吗？为了让我们的二叉查找树高度的期望维持在 log n ，我们就要通过平衡树来进行一些维护。而今天我们就来介绍一种神奇的平衡树——TREAP

写在前面：如果你还不太熟悉二叉查找树，建议先抽空点我学习二叉查找树后再食用这篇BLOG.

什么是Treap

我们都知道，Treap是平衡树的一种实现形式，而平衡树的本质又是一棵二叉查找树，所以Treap拥有二叉查找树的性质，即对于每一个节点，若存在左子节点，那么该节点的值一定大于左子节点的值；若存在右子节点，那么该节点的值一定小于右子节点的值。

Treap=Binary Search Tree+Heap（二叉搜索树+堆） Treap之所以不同于一般的二叉查找树，是因为它除了有满足二叉查找树性质的存储点值，还有一个满足堆性质的随机的附加值(key)。也就是说Treap是一个随机附加域满足堆的性质的二叉搜索树，其结构相当于以随机数据插入的二叉搜索树。其基本操作的期望时间复杂度为O(logn)。相对于其他的平衡二叉搜索树，Treap的特点是实现简单，且能基本实现随机平衡的结构。

那么这个随机的附加值有什么用呢？举个栗子，当我们在插入一个节点时，开始时会像二叉查找树一样先找到一个这个值能放的位置，成为某一个节点下的叶子节点。到这里如果是二叉查找树，插入到这里就结束了。

但是聪明的人类就发现了，如果我一直插入比之前大的数，或者一直比前面小的数，那这棵查找树不就变成一条链了吗？那单次操作就不再是期望的O(log n)，而是O(n)了，那肯定不行啊，于是聪明的人类发明了Treap。

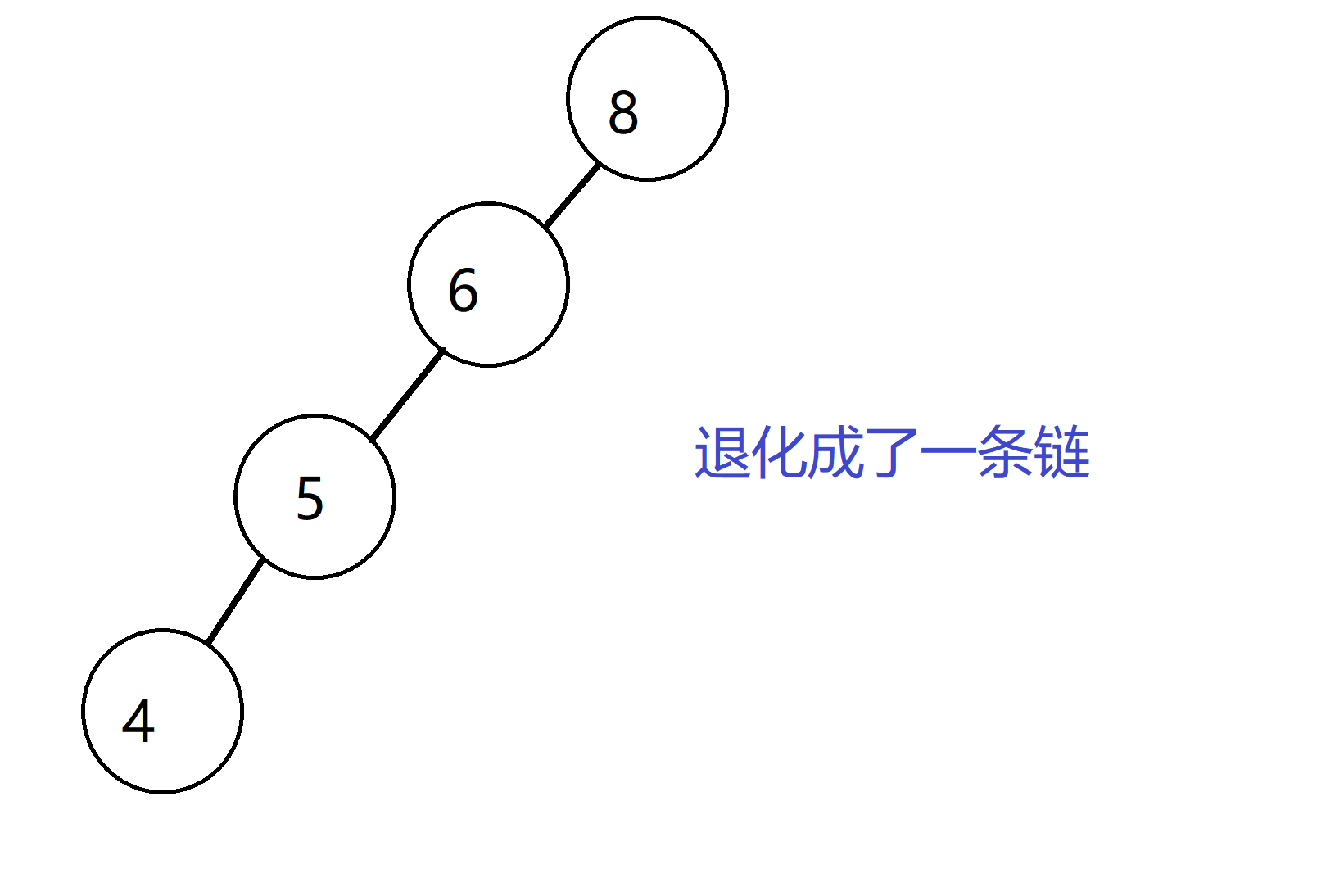
Treap的思想就是，在每一次插入的时候，都会给每个点一个随机的key值，然后让整棵树在满足原本存储的值(val)成一棵二叉查找树外，而外的key值能成为一个堆(大根堆或小根堆)，比如上面那个栗子，如果加入了随机的key值，就可能变成下面这样：

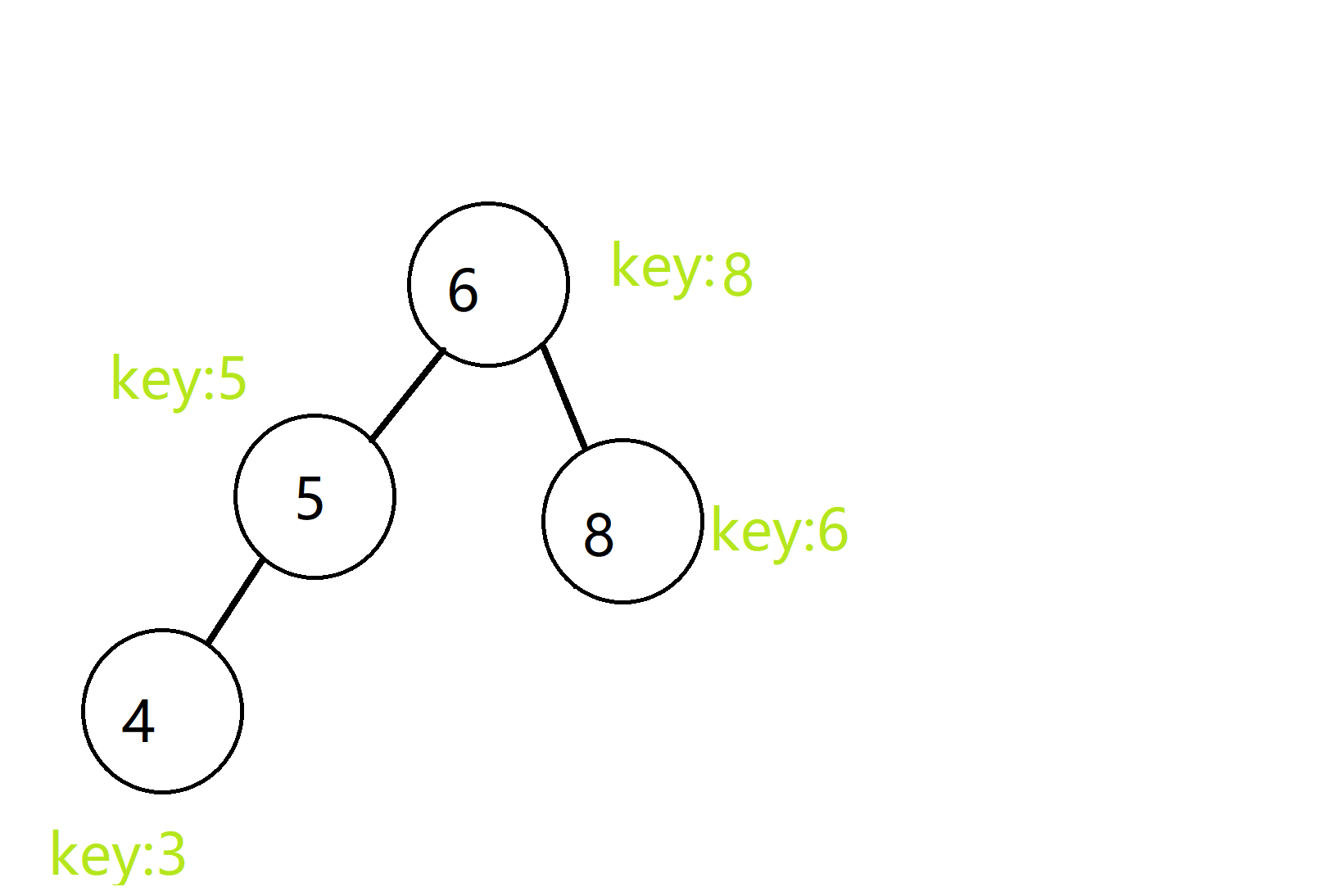
避免了退化成一条链的情况，那么我们要怎么操作才能让这棵树即满足val值形成二叉查找树，又满足key值形成大根堆呢？

这就是我们的精髓——旋转了。

比如在刚开始插入6的时候，他由于比先插入的8小，所以成为了8的左儿子：

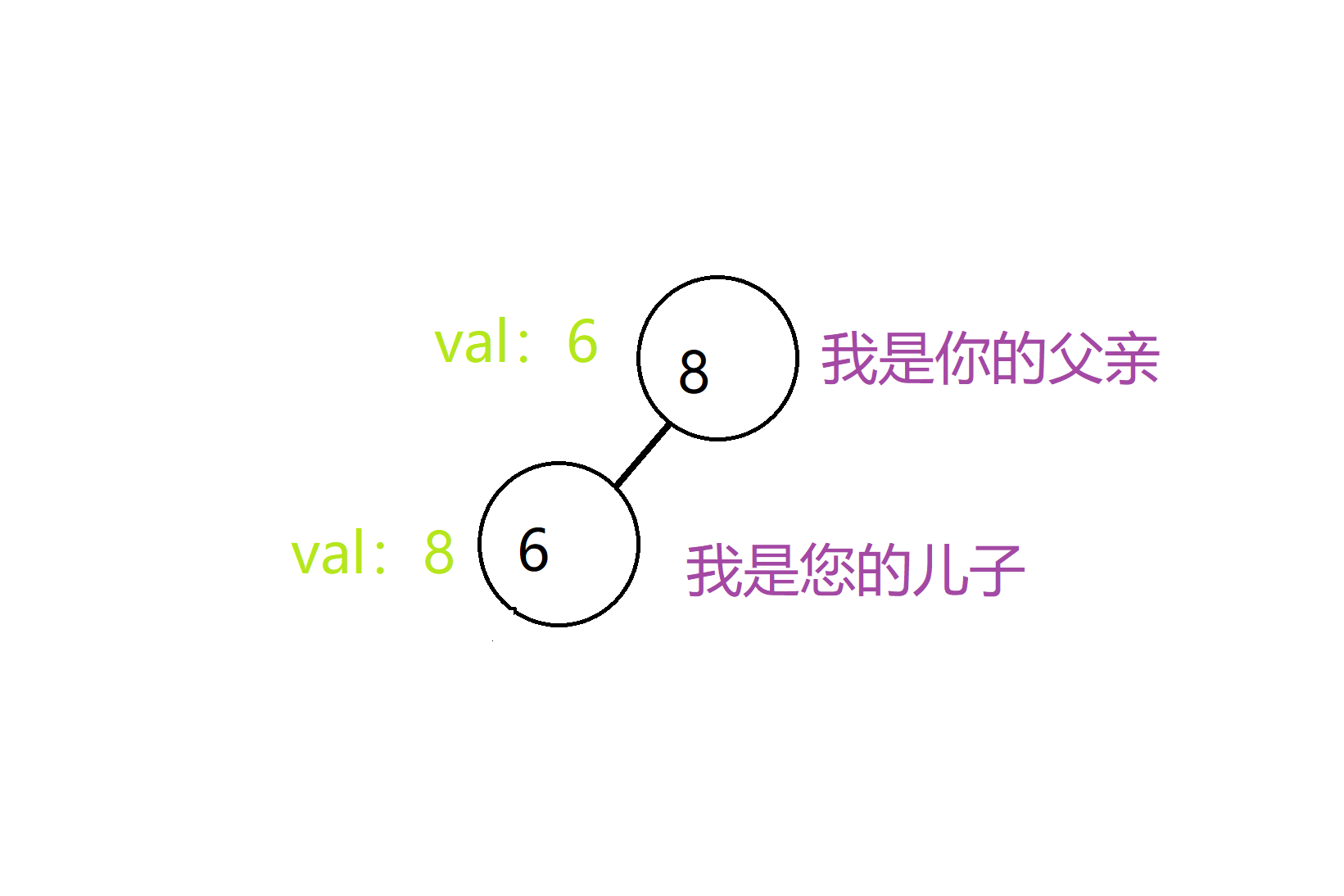
但是这时我们发现随机给到的key值不满足大根堆的性质，所以我们就要在不破坏二叉查找树的性质的前提下，把6旋转向上，成为8的父亲：

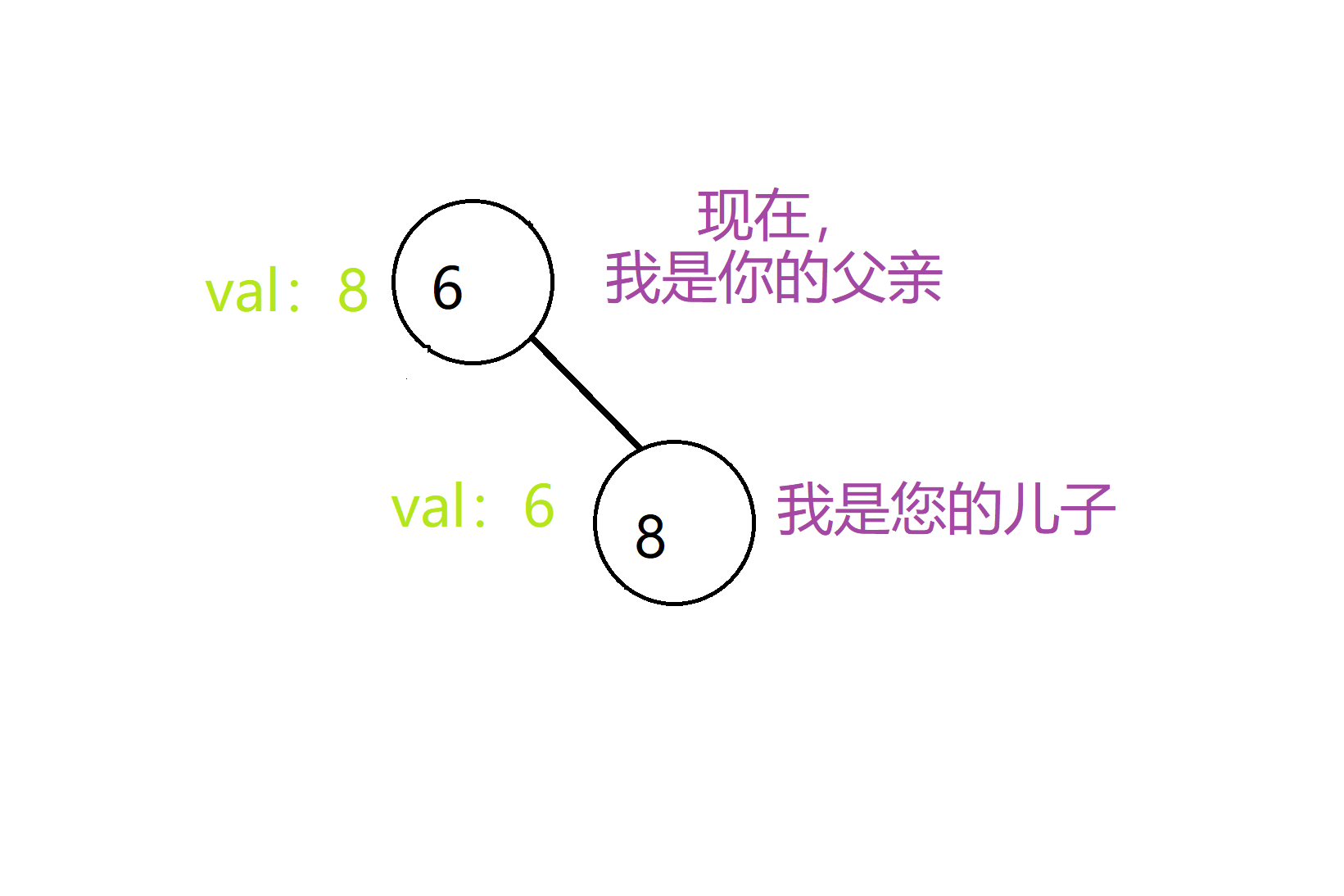
这样我们不停的对新插入的节点向上旋转直到满足堆性质的位置，我们就能完成对堆性质的维护了。

具体来说，旋转分为两种，左旋和右旋，比如我们要把x旋转向上，为了不破坏二叉查找树的性质，那么左旋和右旋是这样的：

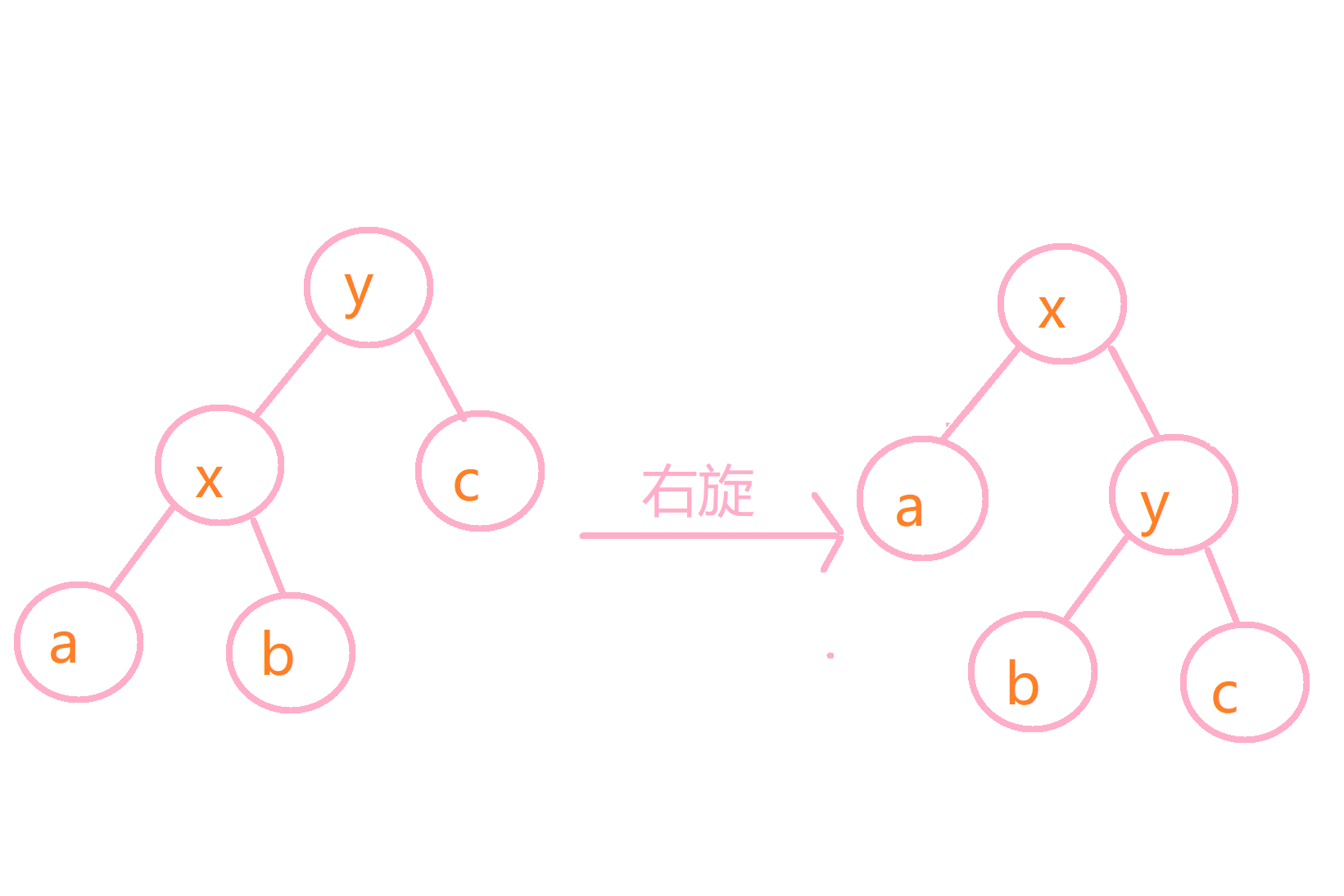
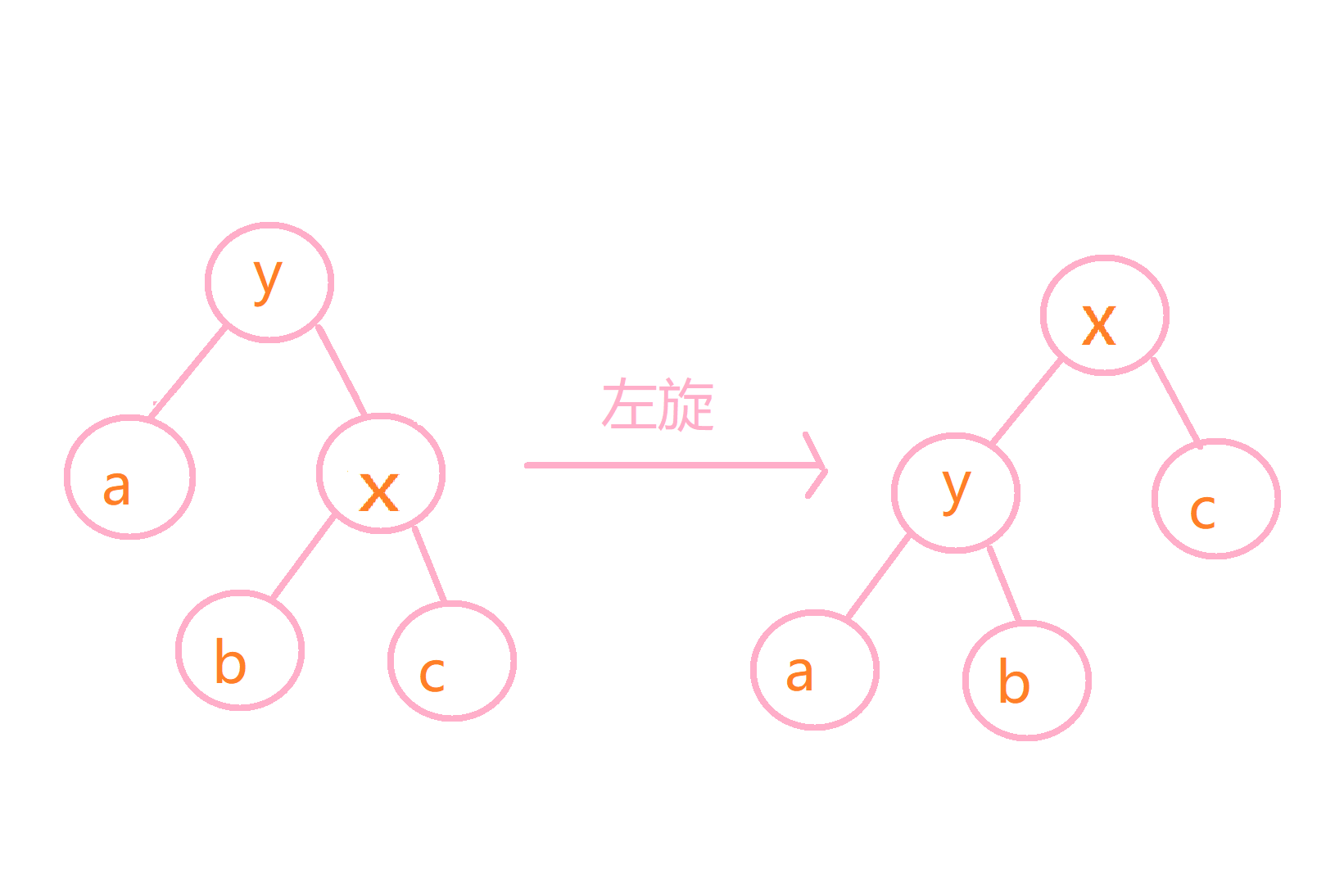
看懂这两幅图，treap的旋转也就理解的差不多了，具体代码如下：

struct trnode
{
    int d,n,c,f,son[2];//d为值，f为父亲编号，c为控制的节点个数，n为同值节点的个数 
}tr[110000];int len;

int update(int x)//更新x控制的节点数 
{
    int lc=tr[x].son[0];
    int rc=tr[x].son[1];
    tr[x].c=tr[lc].c+tr[rc].c+tr[x].n;
}

int rotate(int x,int w)
{
    int f=tr[x].f,ff=tr[f].f;//在旋转之前先确定好x的父亲和爷爷
    //开始旋转建立关系
    int r,R;//r表示儿辈，R表示父辈 

    r=tr[x].son[w],R=tr[x].f;//x的儿子准备当x父亲的新儿子 
    tr[R].son[1-w]=r;
    if(r!=0)tr[r].f=R;

    r=x,R=ff;//x准备当他爷爷新孩子 
    if(tr[R].son[0]==f) tr[R].son[0]=r; else tr[R].son[1]=r;
    tr[r].f=R;

    r=f,R=x;//x的父亲当x的儿子 
    tr[R].son[w]=r; 
    tr[r].f=R; 

    update(f);
    update(x); 
}

FHQ-Treap

上面我们主要介绍了一下什么是Treap，以及如何用旋转来实现Treap，但本篇文章的重点是如何不旋转也能实现Treap呢？FHQ大佬给出了一种精妙的算法。

作为一种平衡树，FHQ Treap不需要旋转！！！而且FHQ Treap代码简短，常数比splay小，支持区间操作，最重要的是可持久化！！听起来就令人激动，那这个神奇的Treap是如何实现的呢？

其实算法的中心只有两个算法——拆分和合并。其他的操作只要灵活的调用一下拆分和合并就可以了，在讲解具体操作之前我们先来了解一下FHQ-Treap。

与普通Treap的异同

与Treap相同，FHQ Treap也维护两个值key和d，key值就是每个节点的随机附加值满足堆的性质（大根或小根），d值就是原本每个节点存储的值，满足二叉搜索树的性质（即对于每一个节点，若存在左子节点，那么该节点的值一定大于左子节点的值；若存在右子节点，那么该节点的值一定小于右子节点的值），这里不再赘述。

与Treap不同的是，这里不再用旋转维护堆的性质，而是在合并的同时维护堆的性质，所以实现了“平衡”，而且这里每个节点只存一个数字，也就是说，n个相同元素会有n个点而不是一个节点记录cnt值表示有多少个相同元素。

核心操作

1.split（拆分）

拆分操作的意思是将一棵以now为根节点的Treap拆成两棵Treap（左树以x为根节点和右树以y为根节点），满足左树的所有值<=d，右树的所有值>d，因为原Treap满足堆的性质，自顶向下拆分后的两个树也会满足堆的性质，所以不需判断，作用将会在之后阐述，具体实现见代码：

void split(int now,int &a,int &b,int d)
{//拆分操作
    //now原Treap，a左树，b右树，d判定值
    //注意传地址符
    if(now==0){
        a=b=0;//若now=0分割完毕；
        return;
    }
    if(tr[now].d<=d)//因为now左子树中的所有值都小于now的值，所以若now属于左树，那么他们都属于左树递归now的右子树；
        a=now,split(tr[now].son[1],tr[a].son[1],b,d);//a=now已经使a的右子树=now的右子树，不再递归a的右子树；
        else//同上now右子树也都属于左树，递归左子树；
        b=now,split(tr[now].son[0],a,tr[b].son[0],d); 
    update(now);//因为后面会用到左（右）树的siz所以更新维护
}

2.merge（合并）

合并操作是将两个Treap a,b(满足a中所有元素均小于b中所有元素，且a以x为根节点，b以y为根节点)，合并成一个Treap，合并的原则是满足堆的性质，所以是一种平衡树，由于是堆的合并，与左偏树有几分类似，感兴趣的同学可以点击这里学习左偏树。

void merge(int &now,int a,int b)
{//合并操作
    //now新树
    if(a==0||b==0){
        now=a+b;//若某个树已空，则将另一个树整体插入
        return;
    }
    //按照key值合并（堆性质）
    if(tr[a].key<tr[b].key)//若a树key值<b树，那么b树属于a树的后代，因为b树恒大于a树，那么b树一定属于a树的右后代，a的左子树不变，直接赋给now，递归合并a的右子树和b
        now=a,merge(tr[now].son[1],tr[a].son[1],b);
    else
        now=b,merge(tr[now].son[0],a,tr[b].son[0]);//同理，a树一定是b树的左儿子，递归合并b的左儿子和a
    update(now);
} 

基本操作

1.随机一个节点的key值

由于在插入一个节点的同时，我们要给它随机一个key值，而c++自带的随机貌似要调用time库才能真正随机，所以我们干脆自己手写一个随机，seed放任意正整数貌似都没有问题。

int seed=233,root=1;

int Rand()//随机key值
{
    return seed=int(seed*482711ll%2147483647);
}

2.新建值为d的节点

这里的操作和二叉查找树一样，就不过多讲述了。

int add(int d)//新建值为d的节点
{
    tr[++len].c=1;
    tr[len].d=d;
    tr[len].key=Rand();
    tr[len].son[0]=tr[len].son[1]=0;
    return len; 
}

3.维护子树大小

在每一次加入或删除节点后，我们都要更新子树的大小，即这颗子树有多少个节点，和二叉查找树的操作一样，也不再过多解释了。

void update(int now)//维护子树大小
{
    tr[now].c=tr[tr[now].son[0]].c+tr[tr[now].son[1]].c+1;
}

4.找第k大的数是谁

由于我们存储的d值满足二叉查找树，所以只要按照二叉查找树的模板递归往下查询就好了，也不再过多解释了。

void find(int now,int rank)
{//找第k大
    while(tr[tr[now].son[0]].c+1!=rank){
        if(tr[tr[now].son[0]].c>=rank)
            now=tr[now].son[0];//若左子树大小大于rank，找左子树
        else
            rank-=(tr[tr[now].son[0]].c+1),now=tr[now].son[1];//找右子树（rank-左子树大小-树根（大小为1））号的元素
    }
    printf("%d\n",tr[now].d);
}

    void get_val(int rank)
{
    find(root,rank);//find查找即可
}

5.插入一个值为d的节点

这个操作就比较有意思了，建议一边看着代码一边来理解：

void insert(int d)
{
    int x=0,y=0,z;
    z=add(d);//新建节点z，作为z树
    split(root,x,y,d);//将树分为两部分，x树为<=待插入值，y树大于
    merge(x,x,z);//合并x树和新节点z（树），赋给x树
    merge(root,x,y);//合并新x树和y树，赋给根
    //就这么简单
}

我们现在要插入一个值为d的点，实现我们先新建一个值为d的点，用指针z指向它，然后我们把这颗Treap分为值小于等于d，和大于d 的两颗Treap，根节点分别为x和y，接着我们加入merge操作，把x和z合并起来，最后把x和y合并起来，就好了。

6.删除一个数

这个操作也比较有意思了，同样的建议一边看着代码一边来理解：

void delet(int d)
{
    int x=0,y=0,z=0;
    split(root,x,y,d);/分为x树为全部小于等于待删除的值，y树大于待删除的值
    split(x,x,z,d-1);//x树分为新x树小于待删除，z树等于待删除
    merge(z,tr[z].son[0],tr[z].son[1]);//合并z树左右儿子，赋给z树，即丢弃z树根节点（实现删除）
    merge(x,x,z);
    merge(root,x,y);//合并，不在重复
}

首先我们先把整颗Treap分为x树为全部小于等于待删除的值和y树大于待删除的值，接着我们再进一步分解，把x树分为新x树小于待删除，z树等于待删除的值。

这时由于z数中所有点的值都等于我们的待删除值，所以我们直接删除掉根节点，合并一下它的左右子树为新z，最后再把x，y，z合并为一棵Treap就好了。

7.获得一个数的排名

这个操作就很简单了，我们只要把原来的一整棵Treap拆分成小于这个数的子树x 和 大于等于这个数的子树y，再统计一下x的大小加一就是我们要的答案了。

void get_rank(int d)
{
    int x=0,y=0;
    split(root,x,y,d-1);//分为小于待查找值的x树和大于等于的y树
    printf("%d\n",tr[x].c+1);//即为待查找值的编号
    merge(root,x,y);//合并
}

8.寻找一个数的前驱

这个也很简单，我们只要拆分出一个小于这个数的子树x，再在x当中找到最大值就好了。

void get_pre(int d)
{
    int x=0,y=0;
    split(root,x,y,d-1);//x树为<=val-1值即小于val值
    find(x,tr[x].c);//在小于val值中找最大的（编号为siz的）就是前驱
    merge(root,x,y);
}

9.寻找一个数的后继

和找前驱一样，我们只要拆分出一个大于这个数的子树x，再在x当中找到最小值就好了。

void get_nxt(int d)
{
    int x=0,y=0;
    split(root,x,y,d);//x树小于等于val值，那么y树大于val值
    find(y,1);//在y树中找最小的，即为后继
    merge(root,x,y);//合并
}

到这里，FHQ-Treap的基本操作就介绍完了。

经典例题

【luogu p3369】
题目描述
您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：

插入 xx 数
删除 xx 数(若有多个相同的数，因只删除一个)
查询 xx 数的排名(排名定义为比当前数小的数的个数 +1+1 。若有多个相同的数，因输出最小的排名)
查询排名为 xx 的数
求 xx 的前驱(前驱定义为小于 xx ，且最大的数)
求 xx 的后继(后继定义为大于 xx ，且最小的数)
输入输出格式
输入格式：
第一行为 nn ，表示操作的个数,下面 nn 行每行有两个数 optopt 和 xx ， optopt 表示操作的序号( 1 \leq opt \leq 6 1≤opt≤6 )

输出格式：
对于操作 3,4,5,63,4,5,6 每行输出一个数，表示对应答案

输入输出样例
输入样例#1：
10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598
输出样例#1：
106465
84185
492737
说明
时空限制：1000ms,128M

1.n的数据范围： n \leq 100000 n≤100000

2.每个数的数据范围： [-{10}^7, {10}^7][−10
7
,10
7
]

这就是一道标准的平衡树题目了，直接给出板子：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std;
struct node
{
    int c,d,key,son[2];
}tr[5500000];int len;

int seed=233,root=1;

int Rand()//随机key值
{
    return seed=int(seed*482711ll%2147483647);
}

int add(int d)//新建值为d的节点
{
    tr[++len].c=1;
    tr[len].d=d;
    tr[len].key=Rand();
    tr[len].son[0]=tr[len].son[1]=0;
    return len; 
}

void update(int now)//维护子树大小
{
    tr[now].c=tr[tr[now].son[0]].c+tr[tr[now].son[1]].c+1;
}

void split(int now,int &a,int &b,int d)
{//拆分操作
    //now原Treap，a左树，b右树，d判定值
    //注意传地址符
    if(now==0){
        a=b=0;//若now=0分割完毕；
        return;
    }
    if(tr[now].d<=d)//因为now左子树中的所有值都小于now的值，所以若now属于左树，那么他们都属于左树递归now的右子树；
        a=now,split(tr[now].son[1],tr[a].son[1],b,d);//a=now已经使a的右子树=now的右子树，不再递归a的右子树；
        else//同上now右子树也都属于左树，递归左子树；
        b=now,split(tr[now].son[0],a,tr[b].son[0],d); 
    update(now);//因为后面会用到左（右）树的siz所以更新维护
}

void merge(int &now,int a,int b)
{//合并操作
    //now新树
    if(a==0||b==0){
        now=a+b;//若某个树已空，则将另一个树整体插入
        return;
    }
    //按照key值合并（堆性质）
    if(tr[a].key<tr[b].key)//若a树key值<b树，那么b树属于a树的后代，因为b树恒大于a树，那么b树一定属于a树的右后代，a的左子树不变，直接赋给now，递归合并a的右子树和b
        now=a,merge(tr[now].son[1],tr[a].son[1],b);
    else
        now=b,merge(tr[now].son[0],a,tr[b].son[0]);//同理，a树一定是b树的左儿子，递归合并b的左儿子和a
    update(now);
} 

void find(int now,int rank)
{//找第k大
    while(tr[tr[now].son[0]].c+1!=rank){
        if(tr[tr[now].son[0]].c>=rank)
            now=tr[now].son[0];//若左子树大小大于rank，找左子树
        else
            rank-=(tr[tr[now].son[0]].c+1),now=tr[now].son[1];//找右子树（rank-左子树大小-树根（大小为1））号的元素
    }
    printf("%d\n",tr[now].d);
}

void insert(int d)
{
    int x=0,y=0,z;
    z=add(d);//新建节点z，作为z树
    split(root,x,y,d);//将树分为两部分，x树为<=待插入值，y树大于
    merge(x,x,z);//合并x树和新节点z（树），赋给x树
    merge(root,x,y);//合并新x树和y树，赋给根
    //就这么简单
}
void delet(int d)
{
    int x=0,y=0,z=0;
    split(root,x,y,d);//分为x树为<=待aaa删除，y树大于
    split(x,x,z,d-1);//x树分为新x树<待删除，z树等于待删除
    merge(z,tr[z].son[0],tr[z].son[1]);//合并z树左右儿子，赋给z树，即丢弃z树根节点（实现删除）
    merge(x,x,z);
    merge(root,x,y);//合并，不在重复
}

void get_rank(int d)
{
    int x=0,y=0;
    split(root,x,y,d-1);//分为小于待查找值的x树和大于等于的y树
    printf("%d\n",tr[x].c+1);//即为待查找值的编号
    merge(root,x,y);//合并
} 
void get_val(int rank)
{
    find(root,rank);//find查找即可
}

void get_pre(int d)
{
    int x=0,y=0;
    split(root,x,y,d-1);//x树为<=val-1值即小于val值
    find(x,tr[x].c);//在小于val值中找最大的（编号为siz的）就是前驱
    merge(root,x,y);
}

void get_nxt(int d)
{
    int x=0,y=0;
    split(root,x,y,d);//x树小于等于val值，那么y树大于val值
    find(y,1);//在y树中找最小的，即为后继
    merge(root,x,y);//合并
}

int main()
{
    int i,j,k,m;root=1;
    add(2147483627);//初始虚节点
    tr[1].c=0;//siz为0，不算虚节点的大小
    scanf("%d",&m);
    for(i=1;i<=m;i++){
        scanf("%d%d",&j,&k);
        if(j==1)insert(k);
        if(j==2)delet(k);
        if(j==3)get_rank(k);
        if(j==4)get_val(k);
        if(j==5)get_pre(k);
        if(j==6)get_nxt(k);
    }
    return 0;
} 

结语

在这里特别感谢洛谷上的大佬 中二攻子，让我一次学会了FHQ-TREAP。希望你在看完这篇BLOG后，也能学会这个实用的数据结构。希望你喜欢这篇BLOG！