【蒟蒻动态规划】人类智慧结晶-浅谈管道取珠一类问题

Author： jvruo
发布时间：August 20, 2021
2182views
No comments
7220字数
Categories：蒟蒻动态规划

在 $NOI2009$ 的赛场上，一道叫《管道取珠》的题目横空出世，以及新颖的解法和独到的思维方法被誉为“人类智慧的结晶”。在之后对这道题的模仿、改编甚至加强一直都没有停下过。不得不承认管道取珠一类问题在 $2021$ 年的今天已经变成非常经典的一类问题了。今天我就结合管道取珠原题和一道 $ICPC$ 区域赛的题目，浅谈一下管道取珠这一类问题的思考方法。

原滋原味[管道取珠]

题目描述

Description

管道取珠是小$X$很喜欢的一款游戏。在本题中，我们将考虑该游戏的一个简单改版。游戏画面如图 $1$ 所示：

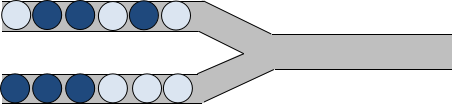
游戏初始时，左侧上下两个管道分别有一定数量的小球（有深色球和浅色球两种类型），而右侧输出管道为空。每一次操作，可以从左侧选择一个管道，并将该管道中最右侧的球推入右边输出管道。

例如，我们首先从下管道中移一个球到输出管道中，将得到图 $2$ 所示的情况：

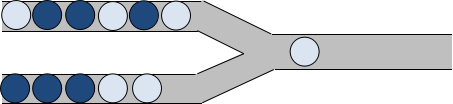
假设上管道中有 $n$ 个球,下管道中有 $m$ 个球，则整个游戏过程需要进行 $n+m$ 次操作，即将所有左侧管道中的球移入输出管道。最终 $n +m$ 个球在输出管道中从右到左形成输出序列。

爱好数学的小$X$知道，他共有 $C_{n+m}^{n}$ 种不同的操作方式，而不同的操作方式可能导致相同的输出序列。举个例子，对于图 $3$ 所示的游戏情形：

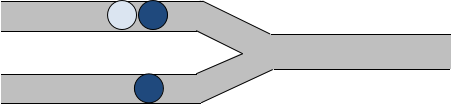
我们用 $A$ 表示浅色球，$B$ 表示深色球。并设移动上管道右侧球的操作为 $U$，移动下管道右侧球的操作为 $D$，则共有 $C_{2+1}^1=3$ 种不同的操作方式,分别为 $UUD$ , $UDU $, $DUU$；最终在输出管道中形成的输出序列（从右到左）分别为 $BAB$， $BBA$， $BBA$。可以发现后两种操作方式将得到同样的输出序列。

假设最终可能产生的不同种类的输出序列共有 $K$ 种，其中第 $i$ 种输出序列的产生方式(即不同的操作方式数目)有 $a_i$ 个。聪明的小$X$早已知道，$\sum_{i=1}^k a_i = C_{n+m}^{n}$，因此小$X$希望计算得到 $\sum_{i=1}^k a_i^2$。你能帮助他计算这个值么？由于这个值可能很大，因此只需要输出该值对 $1024523$ 的取模即可(即除以 $1024523$ 的余数)。

说明：文中 $C_{n+m}^{n}$ 表示组合数。组合数 $C_{a}^{b}$ 等价于在 $a$ 个不同的物品中选取 $b$ 个的选取方案数。

Input

第一行包含两个整数 $n,m(n, m \le 500)$，分别表示上下两个管道中球的数目。

第二行为一个 $AB$ 字符串，长度为 $n$，表示上管道中从左到右球的类型。其中 $A$ 表示浅色球，$B$ 表示深色球。

第三行为一个 $AB$ 字符串，长度为 $m$ ，表示下管道中的情形。

Output

仅包含一行，即为 $\sum_{i=1}^k a_i^2$ 除以 $1024523$ 的余数。

Sample Input

2 1
AB
B

Sample Output

解题思路

首先我没观察数据范围，由于 $n,m \le 500$，我们不可能算出所有的 $a_i$。我们的突破口是具$\sum_{i=1}^k a_i^2$体代表的是什么？或者换句话说，我没有没有什么东西的物理意义就是 $\sum_{i=1}^k a_i^2$？

第一次接触这类问题的同学非常难想到，这里我就直接揭晓答案了，这其实代表的是如果有两个一模一样的装置同时进行取珠子的操作，这两个装置取得相同的序列的方案数是多少：

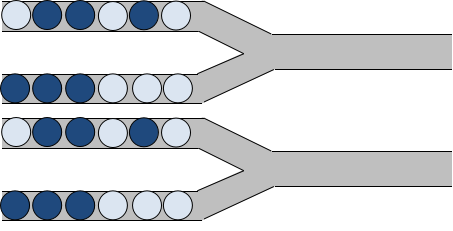
这是因为对于第一个装置的取出的一种序列假设为第 $i$ 种，在第二种序列中恰好有 $a_i$ 种与其对应，所以稍微写写画画就发现总的贡献就是 $\sum_{i=1}^k a_i^2$。

这时我们最朴素的方法就是设 $f[i][j][k][l]$ 表示第一个装置上面出来了 $i$ 个，下面出来了 $j$ 个并且第二个装置上面出来了 $k$ 个，下面出来了 $l$ 个出来的珠子相同的方案数。接下来我们考虑怎么转移：

$a[i] == a[k]$ 时，$f[i][j][k][l] += f[i - 1][j][k - 1][l]$；
$a[i] == a[l]$ 时，$f[i][j][k][l] += f[i - 1][j][k][l - 1]$；
$a[j] == a[k]$ 时，$f[i][j][k][l] += f[i][j - 1][k - 1][l]$；
$a[j] == a[l]$ 时，$f[i][j][k][l] += f[i][j - 1][k][l - 1]$。

当然这样做我没的时空复杂度都是 $O(n^4)$，是顶不足的。但是我们的 $i,j,k,l$ 有 $i + j = k + l$，所以我们可以该状态为 $f[x][i][k]$ 示第一个装置上面出来了 $i$ 个，并且第二个装置上面出来了 $k$ 个，两个装置都出了 $x$ 个珠子并且出来的珠子相同的方案数，这样我没的时空复杂度就变成了 $O(n^3)$，这样我们的时间复杂度就对了，转移也是一样的道理。但这时我们的空间还是有点大，同样的我们发现 $x$ 这一维度是可以滚动的，这样我们的状态就变成了 $f[0/1][i][k]$，空间也过得去了。

这道题后面的 $DP$ 过程其实是不难的，难的是我们对于 $\sum_{i=1}^k a_i^2$ 转化为两个一模一样的装置同时进行取珠子的操作，这两个装置取得相同的序列的方案数是多少这个模型转化的这一步。在这一题之后，出现了非常非常多无趣的改编题，但思路都是考虑多几个装置会怎么样，举一反三就可以了。

代码实现

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
const int MOD = 1024523;
int f[2][550][550];
char a[550], b[550];
int lena, lenb;
int main() {
    memset(f, 0, sizeof(f));
    scanf("%d%d", &lena, &lenb);
    scanf("%s", a + 1);
    scanf("%s", b + 1);
    f[0][0][0] = 1;

    for(int x = 1; x <= lena + lenb; x++) {
        for(int i = 0; i <= min(x, lena); i++) {
            for(int k = 0; k <= min(x, lena); k++) {
                f[x % 2][i][k] = 0;
                if(i > 0 && k > 0 && a[i] == a[k]) f[x % 2][i][k] = (f[x % 2][i][k] + f[(1 - x % 2)][i - 1][k - 1]) % MOD;
                if(i > 0 && x - k > 0 && a[i] == b[x - k]) f[x % 2][i][k] = (f[x % 2][i][k] + f[(1 - x % 2)][i - 1][k]) % MOD;
                if(x - i > 0 && k > 0 && b[x - i] == a[k]) f[x % 2][i][k] = (f[x % 2][i][k] + f[(1 - x % 2)][i][k - 1]) % MOD;
                if(x - i > 0 && x - k > 0 && b[x - i] == b[x - k]) f[x % 2][i][k] = (f[x % 2][i][k] + f[(1 - x % 2)][i][k]) % MOD;
            }
        }
    }

    printf("%d", f[(lena + lenb) % 2][lena][lena]);
    return 0;
}

新装升级[灯谜]

题目描述

Description

小蒟蒻在探险的时候发现了一个奇怪的游戏，这个游戏有 $n$ 盏灯，每盏灯刚开始都是熄灭的。有灯那么必然就有开关，小蒟蒻在另外一侧发现了 $m$ 个开关，对于每个开关，都控制着一定数量的灯。对于每个开关，小蒟蒻可以选择按一下，或者不按，每次按下，这个开关都会让其控制的灯的状态取反。
设 $x$ 是最后亮着的灯的个数，现在需要求 $E(x^3) * 2^m$ 的值，$E$ 表示取期望。只需要输出在模 $10^9 + 7$ 意义下的答案。

Input

第一行两个整数 $n,m(n, m \le 50)$。

接下来 $m$ 行，每行开头一个整数 $k(k \le n)$ 表示第 $i$ 个开关控制的灯的个数，接下来 $k$ 个整数表示控制的灯的编号。

Output

输出一个整数表示答案。

Sample Input

4 2
3 1 2 4
2 3 4

Sample Output

解题思路

首先要知道 $E(x^3) \ne (E(x))^3$，要不然这道题做法就不对了。

这是一道区域赛真题改编，当时很多前排队伍没出但是有中游队伍直接 $rush$ 过，区别就在于中游队伍可能做过我们上面那题管道取珠。要解决这个问题，我们要先理解为什么出题人要我们算 $E(x ^3)*2^m$ 而不是算 $E(x^3)$？这一点其实就是我们突破问题找到思路的一个突破口。这是因为我们的 $E(x^3)$ 其实是所有情况的一个加权平均值，而分母恰好就是所有情况的数量也就是每个开关按或者不按也就是 $2^m$。所以其实问题的本质就是求所有情况下的开灯情况的一个累加和也就是 $\sum X^3$。

我们令 $X = (x_1 + x_2 + …… + x_n)$，$x_i$ 是第 $i$ 个灯的开闭情况，$x_i = 1$ 代表第 $i$ 个灯是亮着的，$x_i = 0$ 代表第 $i$ 个灯是灭着的。那 $X^3 = (x_1 + x_2 + …… + x_n)^3$，我们还是要考虑这个 $X^3$ 的一个物理意义。这道题和我们之前的管道取珠以及很多无趣的改编题的区别就在于这题当中的物理含义不再是加几套一模一样的装置然后看最后相同的方案数了。在这道题种代表的物理含义其实是对于任意三个灯(可以重复) $x_i,x_j,x_k$，它们都亮着的时候会给答案贡献一个 $1$。

这是因为 $X^3 = (x_1 + x_2 + …… + x_n)^3$，而 $$(x_1 + x_2 + …… + x_n)^3 = (x_1 + x_2 + …… + x_n)*(x_1 + x_2 + …… + x_n)*(x_1 + x_2 + …… + x_n)$$。我们把这个式子展开就可以发现是任意三项乘积的累加和，而 $x_i = 0/1$，也就是说这就是对于任意三个灯(可以重复) $x_i,x_j,x_k$，它们都亮着的时候才会给答案贡献一个 $1$。

所以我们任意枚举三个灯 $x_i,x_j,x_k$，我们 $DP$ 计算有多少种按开关方案使得最后这三个灯都亮着。所以我们设 $F[t][st]$ 表示前 $t$ 个按钮 $x_i,x_j,x_k$ 三个灯亮灭情况为 $st$ 的方案数。考虑第 $t$ 个按钮按还是不按，如果不按，就是 $f[t][st] += f[t - 1][st]$；如果按了就是 $f[t][st] += f[t-1][st']$，其中 $st$ 为 $st'$ 的基础上按了第 $t$ 个按钮发生的变化。所以答案就是 $\sum f[i][7]$。

当然这道题时间还是卡的很紧的，如果三个灯 $x_i,x_j,x_k$ 都从 $1$ 到 $n$ 枚举的话会 $TLE$ 的，我们可以枚举 $i \le j \le k$，然后如果 $i = j = k$，那 $ans += f$；如果 $i, j, k$ 中有且仅有两个相等，那么 $ans += 3 * f$ 如果 $i,j,k$ 两两不等，那 $ans += 6 * f$，这样就能优化常数，最后 $AC$。

这道题作为改编题，跳出了多套相同系统的局限，聚焦于一套系统的许多点之间的关系，还巧妙的设置范围让我们能够使用状压$DP$解决这道问题，清新脱俗不愧是改编当中非常有意思的一道题。

代码实现

#include <cmath>
#include <cstdio> 
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
const int MOD = 1e9 + 7;
int a[55][55], num[55], f[55][8], ans;
int n, m;
int main() {
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= m; i++) {
        scanf("%d", &num[i]);
        for(int j = 1; j <= num[i]; j++) scanf("%d", &a[i][j]);
    }

    ans = 0;
    for(int i = 1; i <= n; i++) {
        for(int j = i; j <= n; j++) {
            for(int k = j; k <= n; k++) {
                f[0][0] = 1;
                for(int t = 1; t <= m; t++) {
                    for(int st = 0; st <= 7; st++) {
                        f[t][st] = 0;
                        f[t][st] = (f[t][st] + f[t - 1][st]) % MOD;

                        int temp_st = st;
                        for(int o = 1; o <= num[t]; o++) {
                            if(a[t][o] == i) temp_st ^= 4;
                            if(a[t][o] == j) temp_st ^= 2;
                            if(a[t][o] == k) temp_st ^= 1;
                        } 
                        f[t][st] = (f[t][st] + f[t - 1][temp_st]) % MOD;
                    }
                }
                if(i == j && j == k) ans = (ans + f[m][7]) % MOD;
                else if(j > i && k > j) ans = (ans + 6ll * f[m][7] % MOD) % MOD;
                else ans = (ans + 3ll * f[m][7] % MOD) % MOD;
            }
        }
    }

    printf("%d", ans);
    return 0;
 }

结语

通过这篇 $BLOG$，相信你已经对管道取珠问题有了自己的理解。我相信管道取珠这一经典思想以后还会以各种变型出现在我们的算法竞赛的赛场上，但也不要害怕，其本质都是通过挖掘所求量的物理意义化繁为简，希望这篇 $BLOG$ 能给你这种思想的一点点启发。最后希望你喜欢这篇 $BLOG$ ！

Last modification：August 20th, 2021 at 09:18 pm

If you think my article is useful to you, please feel free to appreciate

【蒟蒻动态规划】人类智慧结晶-浅谈管道取珠一类问题

jvruo • 2021 年 08 月 20 日

在 $NOI2009$ 的赛场上，一道叫《管道取珠》的题目横空出世，以及新颖的解法和独到的思维方法被誉为“人类智慧的结晶”。在之后对这道题的模仿、改编甚至加强一直都没有停下过。不得不承认管道取珠一类问题在 $2021$ 年的今天已经变成非常经典的一类问题了。今天我就结合管道取珠原题和一道 $ICPC$ 区域赛的题目，浅谈一下管道取珠这一类问题的思考方法。

原滋原味[管道取珠]

题目描述

Description

管道取珠是小$X$很喜欢的一款游戏。在本题中，我们将考虑该游戏的一个简单改版。游戏画面如图 $1$ 所示：

例如，我们首先从下管道中移一个球到输出管道中，将得到图 $2$ 所示的情况：

爱好数学的小$X$知道，他共有 $C_{n+m}^{n}$ 种不同的操作方式，而不同的操作方式可能导致相同的输出序列。举个例子，对于图 $3$ 所示的游戏情形：

说明：文中 $C_{n+m}^{n}$ 表示组合数。组合数 $C_{a}^{b}$ 等价于在 $a$ 个不同的物品中选取 $b$ 个的选取方案数。

Input

第一行包含两个整数 $n,m(n, m \le 500)$，分别表示上下两个管道中球的数目。

第二行为一个 $AB$ 字符串，长度为 $n$，表示上管道中从左到右球的类型。其中 $A$ 表示浅色球，$B$ 表示深色球。

第三行为一个 $AB$ 字符串，长度为 $m$ ，表示下管道中的情形。

Output

仅包含一行，即为 $\sum_{i=1}^k a_i^2$ 除以 $1024523$ 的余数。

Sample Input

2 1
AB
B

Sample Output

解题思路

$a[i] == a[k]$ 时，$f[i][j][k][l] += f[i - 1][j][k - 1][l]$；
$a[i] == a[l]$ 时，$f[i][j][k][l] += f[i - 1][j][k][l - 1]$；
$a[j] == a[k]$ 时，$f[i][j][k][l] += f[i][j - 1][k - 1][l]$；
$a[j] == a[l]$ 时，$f[i][j][k][l] += f[i][j - 1][k][l - 1]$。

代码实现

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
const int MOD = 1024523;
int f[2][550][550];
char a[550], b[550];
int lena, lenb;
int main() {
    memset(f, 0, sizeof(f));
    scanf("%d%d", &lena, &lenb);
    scanf("%s", a + 1);
    scanf("%s", b + 1);
    f[0][0][0] = 1;

    for(int x = 1; x <= lena + lenb; x++) {
        for(int i = 0; i <= min(x, lena); i++) {
            for(int k = 0; k <= min(x, lena); k++) {
                f[x % 2][i][k] = 0;
                if(i > 0 && k > 0 && a[i] == a[k]) f[x % 2][i][k] = (f[x % 2][i][k] + f[(1 - x % 2)][i - 1][k - 1]) % MOD;
                if(i > 0 && x - k > 0 && a[i] == b[x - k]) f[x % 2][i][k] = (f[x % 2][i][k] + f[(1 - x % 2)][i - 1][k]) % MOD;
                if(x - i > 0 && k > 0 && b[x - i] == a[k]) f[x % 2][i][k] = (f[x % 2][i][k] + f[(1 - x % 2)][i][k - 1]) % MOD;
                if(x - i > 0 && x - k > 0 && b[x - i] == b[x - k]) f[x % 2][i][k] = (f[x % 2][i][k] + f[(1 - x % 2)][i][k]) % MOD;
            }
        }
    }

    printf("%d", f[(lena + lenb) % 2][lena][lena]);
    return 0;
}

新装升级[灯谜]

题目描述

Description

Input

第一行两个整数 $n,m(n, m \le 50)$。

接下来 $m$ 行，每行开头一个整数 $k(k \le n)$ 表示第 $i$ 个开关控制的灯的个数，接下来 $k$ 个整数表示控制的灯的编号。

Output

输出一个整数表示答案。

Sample Input

4 2
3 1 2 4
2 3 4

Sample Output

解题思路

首先要知道 $E(x^3) \ne (E(x))^3$，要不然这道题做法就不对了。

代码实现

#include <cmath>
#include <cstdio> 
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
const int MOD = 1e9 + 7;
int a[55][55], num[55], f[55][8], ans;
int n, m;
int main() {
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= m; i++) {
        scanf("%d", &num[i]);
        for(int j = 1; j <= num[i]; j++) scanf("%d", &a[i][j]);
    }

    ans = 0;
    for(int i = 1; i <= n; i++) {
        for(int j = i; j <= n; j++) {
            for(int k = j; k <= n; k++) {
                f[0][0] = 1;
                for(int t = 1; t <= m; t++) {
                    for(int st = 0; st <= 7; st++) {
                        f[t][st] = 0;
                        f[t][st] = (f[t][st] + f[t - 1][st]) % MOD;

                        int temp_st = st;
                        for(int o = 1; o <= num[t]; o++) {
                            if(a[t][o] == i) temp_st ^= 4;
                            if(a[t][o] == j) temp_st ^= 2;
                            if(a[t][o] == k) temp_st ^= 1;
                        } 
                        f[t][st] = (f[t][st] + f[t - 1][temp_st]) % MOD;
                    }
                }
                if(i == j && j == k) ans = (ans + f[m][7]) % MOD;
                else if(j > i && k > j) ans = (ans + 6ll * f[m][7] % MOD) % MOD;
                else ans = (ans + 3ll * f[m][7] % MOD) % MOD;
            }
        }
    }

    printf("%d", ans);
    return 0;
 }

原滋原味[管道取珠]

题目描述

Description

Input

Output

Sample Input

Sample Output

解题思路

代码实现

新装升级[灯谜]

题目描述

Description

Input

Output

Sample Input

Sample Output

解题思路

代码实现

结语