第一次出模拟题很紧张啊……大部分都有原题,但是背景故事测试数据自定义比较器之类的什么的都是我苦苦冥想出来的QwQ。最后说一句,出题目真的好累啊,下面就让我们一起看DAY1的题目吧。
T1 木薯魔王(cassava)
题目部分
【问题描述】
很久很久以前,在一个叫坚果国的国度里,诞生了一个魔王,一个真正的魔王——他以抢夺村民们的木薯为乐,村民们敢怒而不敢言。久而久之,人们就称呼他为“木薯魔王”。
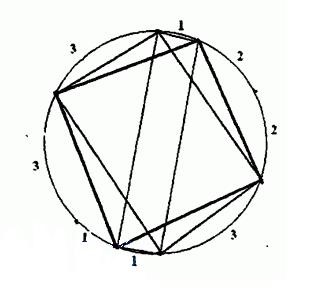
这天,木薯魔王又来到了一户名叫蒟蒻的农户家,他一眼就看上了蒟蒻家中的肥美的木薯,但是魔王毕竟是魔王,直接拿走全部的木薯不够优雅,所以他想玩一些花样。我们已知蒟蒻家的木薯地为圆形,在田地的圆周上插了n个篱笆,如果有四个篱笆能围成矩形那么我们就称其围成的矩形区域为X区域,而木薯魔王只会取X区域内的木薯。所以木薯魔王想知道,在这块木薯地上,有多少块不同的X区域?
换句话说,给出圆周上的若干个点,已知点与点之间的弧长,其值均为正整数,并依圆周顺序排列。请找出这些点中有没有可以围成矩形的,并希望在最短时间内找出所有不重复矩形,输出矩形的个数。
【输入格式】
从文件 cassava.in 中读入数据。
输入的第一行包含一个正整数 n(n≤100) ,表示篱笆的数量。
接下来n行,每行一个Ai(Ai≤1e6)分别为这n个点所分割的各个圆弧长度
【输出格式】
输出到文件 cassava.out 中。输出一个整数,表示篱笆所构成不重复矩形的个数。
【样例 1 输入】
8
1
2
2
3
1
1
3
3
【样例 1 输出】
3
【样例 1 说明】
见下图:
解题思路
这道题作为DAY1的签到题肯定是非常简单的啦。虽然看起来好像是非常复杂的计算几何,但如果我们换一个思路去想这道题就超级简单。
首先我们知道,在一个圆上,只有直径所对应的圆周角为90°,其次在一个矩形当中,任意角都为90°。所以我们就能推出,在圆内构成矩形的对角线定为两条互不重合的直径!所以我们只要通过题目所给出的任意相邻两点间的弧长这个条件,就能求出有多少条直径了,又因为Ai不为0,所以没有重合的直径。根据排列组合,我们要从i条直径当中选两条直径组成矩形的两条对角线,所以我们最后的答案ans关于直径的条数i的关系就是ans=i*(i-1)/2。当然,在直径的条数i≤1的时候,是无法构成矩形的,所以输出0。
难度在普及左右。
程序实现
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
int a[22],s[22];
int i,j,k,m,n,o,p,js,jl,jk;
int main()
{
FILE *fin,*fout;
fin=fopen("cassava.in","rb");
fout=fopen("cassava.out","wb");
fscanf(fin,"%d",&n);
for(int i=1;i<=n;i++)
{
fscanf(fin,"%d",&a[i]);
s[i]=s[i-1]+a[i];
}
if(s[n]%2==1)
{
fprintf(fout,"0");
fclose(fin);
fclose(fout);
exit(0);
}
jl=0;
for(int i=1;i<=n;i++)
{
if(s[i]>s[n]/2)break;
for(int j=1;j<=n;j++)if(s[j]-s[i]==s[n]/2)jl++;
}
fprintf(fout,"%d",jl*(jl-1)/2);
fclose(fin);
fclose(fout);
return 0;
}T2 蒟蒻(konjac)
题目部分
【问题描述】
我们的蒟蒻农夫回到家后,发现自己种的木薯全部都被木薯魔王抢去了,这就意味着他没办法拿着这些木薯去换购《荒野大坚果Ⅱ》了。怒发冲冠的蒟蒻决定带上他祖传的尚方宝剑,变身成为蒟蒻勇士,前往木薯国王的城堡去讨伐木薯魔王。
我们的蒟蒻勇士是一点超能力都没有的,但是幸运的是在路上蒟蒻看到了nm座魔法山峰,这nm座山峰恰好分布在n*m的矩形上。每座山峰都有他自己的高度h[i][j],而且每个山峰的山顶上都有一点能量值。为了打败木薯魔王,蒟蒻勇者必须收集尽可能多的能量值。由于得到了风神的庇护,开始时蒟蒻勇者可以传送到任意一座山峰的山顶上,由于体力不支,蒟蒻勇者没办法往高处爬了,所以接下来的每一步,蒟蒻勇者只能选择其当前所在山峰的上下左右的四座山峰中比当前所在山峰矮的山峰(即严格小于当前山峰高度的山峰)滚过去,现在蒟蒻勇者想知道,他最多能得到多少能量值。
下面是一个例子:
1 2 34 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
我们的蒟蒻勇者可以从某个点滚向上下左右相邻四个点之一,当且仅当高度减小。在上面的例子中,一条可行的路径为24-17-16-1(从24开始,在1结束),这样蒟蒻勇者可以得到四点能量值。当然25-24-23-...-3-2-1更长,这样我们的蒟蒻勇者可以得到25点能量值。事实上,这是最优的一条。
【输入格式】
从文件konjac.in中读入数据。
输入的第一行为表示魔法山峰区域的二维数组的行数R和列数C(1≤R,C≤1000)。 下面是R行,每行有C个数,代表每座魔法山峰的高度(两个数字之间用1个空格间隔)。
【输出格式】
输出到文件konjac.out中。
输出 1 行 1 个整数,表示蒟蒻勇士能获得的最大能量值。
【样例 1 输入】
5 5
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
【样例 1 输出】
25
解题思路
这道题作为DAY1的T2,虽然比T1略难,但还是一道超级大水题。这道题有动态规划和记忆化搜索两种写法,下面就来讲解一下记忆化搜索的想法。
很明显,题目想让我们求的就是一个二位矩阵里的最长下降路径。那我们的想法就很简单了,我们定义f[i][j]为以第i行第j个点为起点的最长下降路径的长度,初始值f[i][j]=1。那么接下来就很简单了,我们从头开始枚举每一个点,如果我们枚举到的这个点(i,j)的f[i][j]=1,那么就代表这个点可能还没处理过哦,那我们就以这个点为起点,深搜出以它为起点的最长下降路径的长度,在深搜的过程中,我们又会顺便更新走到路径上的f[i][j]值,如果在以后的访问中又访问到了这个点,就直接返回f[i][j]值即可。又由于f[i][j]记忆化的存在,每个点最多只处理一次。
所以总的时间复杂度为O(n*m)。难度定在普及+/提高-。
程序实现
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
int f[1100][1100],g[1100][1100];
int i,j,k,m,n,o,p,js,jl,jk,ans;
int my_max(int x,int y)
{
if(x>y)return(x);
else return(y);
}
void find(int u,int v)
{
if(f[u][v]>1)return;
if(u>1 && g[u-1][v]<g[u][v])
{
find(u-1,v);
f[u][v]=my_max(f[u][v],f[u-1][v]+1);
}
if(u<n && g[u+1][v]<g[u][v])
{
find(u+1,v);
f[u][v]=my_max(f[u][v],f[u+1][v]+1);
}
if(v>1 && g[u][v-1]<g[u][v])
{
find(u,v-1);
f[u][v]=my_max(f[u][v],f[u][v-1]+1);
}
if(v<m && g[u][v+1]<g[u][v])
{
find(u,v+1);
f[u][v]=my_max(f[u][v],f[u][v+1]+1);
}
return ;
}
int main()
{
FILE *fin,*fout;
fin=fopen("konjac.in","rb");
fout=fopen("konjac.out","wb");
fscanf(fin,"%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
fscanf(fin,"%d",&g[i][j]);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
f[i][j]=1;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(f[i][j]==1)find(i,j);
ans=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(f[i][j]>ans)ans=f[i][j];
fprintf(fout,"%d",ans);
fclose(fin);
fclose(fout);
return 0;
}T3 咕咕鸡(guguchicken)
题目部分
【问题描述】
得到了233333点能量值的蒟蒻勇者终于来到了木薯魔王的城堡,而木薯魔王作为一只有品位的魔王,他城堡的门口肯定是有高大勇猛的守卫的。果不其然,我们的蒟蒻勇者前脚刚到城堡门口,就见到了魔王最强大的守卫——一只咕咕鸡。以我们蒟蒻勇者的力量是肯定无法正面刚过咕咕鸡的,正在其一筹莫展之际,咕咕鸡主动走了上来,说道:“年轻的勇者哦,我敬佩你的勇气,有鉴于魔王昨天把我的新买的SP4和《荒野大坚果Ⅱ》抢走了,所以我打算祝你一臂之力!”
还没等蒟蒻勇者答应,咕咕鸡又说道:“但是我必须考验一下你有没有资格成为我的新主人,我给你个问题吧——”
“对于一个给定的序列S={a1,a2,a3,…,an},若P={ax1,ax2,ax3,…,axn} ,且满足条件x1<x2<…<xm且ax1<ax2<ax3<…,axn 。那么就称P为S的一个上升序列。如果有多个P满足条件,那么我想你告诉我字典序最小的那个。”
蒟蒻勇者点了点头,陷入了沉思……
简而言之,给出S序列,给出若干询问。对于第i个询问,求出长度为Li的上升序列,如有多个,求出字典序最小的那个(即首先x1最小,如果不唯一,再看x2最小……),如果不存在长度为Li的上升序列,则打印Impossible.
【输入格式】
从文件guguchicken.in中读入数据。
第一行一个整数N,表示序列一共有N(N≤5000)个元素。
第二行N个数,为a1, a2 , ……,an。
第三行一个M(M≤30000),表示询问次数。
下面接M行每行一个数Li,表示要询问长度为Li的上升序列。
【输出格式】
输出到文件guguchicken.out中。
每个询问输出一行,对于每个询问,如果对应的序列存在,则输出,否则打印Impossible.
【样例 1 输入】
6
3 4 1 2 3 6
3
6
4
5
【样例 1 输出】
Impossible
1 2 3 6
Impossible
解题思路
这道题就是一道很经典的DP题了,题目要我们求的就是一个长度为L的字典序最小的最长上升子序列。刚开始想,我们会觉得,好像正着做不太好做。所以我们先从后往前用二分或者树状数组之类的用n log n倒着做一次最长下降子序列,我们定义f[i]为倒着做时,以序列中第i个数字结尾的最长下降子序列的长度(初始化f[n]=1)——即我们求出的就是在原序列中以该位置开头的最长上升子序列的长度。
那么接下来就很简单了,我们只需要从前往后扫一遍。当我们枚举到第i个数的时候,我们先设上一个输出的值是last,现在已经输出了k个数,那么只需要a[i]>last(a[i]表示第i个数的值)且f[i]≥L-last,那么这个点就是合法的,就输出这个点,并且更新last和k++。最后记得特判Impossible的情况
其实这道题只要理解了题目中字典序最小的含义就很简单了。难度定在提高。
程序实现
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
int a[11000],d[11000],f[11000];
int i,j,k,m,n,o,p,js,jl,jk,ans,cnt=1,len;
int find(int l,int r)
{
if(r-l==1)return(l);
int mid=(l+r)/2;
if(d[mid]>js)return(find(mid,r));
else return(find(l,mid));
}
int main()
{
FILE *fin,*fout;
fin=fopen("guguchicken.in","rb");
fout=fopen("guguchicken.out","wb");
fscanf(fin,"%d",&n);
for(int i=1;i<=n;i++)fscanf(fin,"%d",&a[i]);
d[1]=a[n];f[n]=1;d[0]=2147483647; //初始化
int len=1;
for (int i=n-1;i>=1;i--)
{
if (a[i]<d[len])
{
d[++len]=a[i];
f[i]=len;
}
else
{
js=a[i];int j=find(0,len+1)+1;
f[i]=j;
d[j]=a[i];
}
}
//for(int i=1;i<=n;i++)printf("%d ",f[i]);
fscanf(fin,"%d",&m);
for(int i=1;i<=m;i++)
{
fscanf(fin,"%d",&o);jl=0;
if(o>len)fprintf(fout,"Impossible\n");
else
{
for(int j=1;j<=n;j++)if(f[j]>=o && a[j]>jl)
{
if(o>1)fprintf(fout,"%d ",a[j]);
else fprintf(fout,"%d\n",a[j]);
jl=a[j];
o--;if(o==0)break;
}
}
}
fclose(fin);
fclose(fout);
return 0;
}T4 蒟蒻棋(konjacchess)
题目部分
【问题描述】
得到了咕咕鸡的帮助后,我们的蒟蒻勇者终于进入了木薯魔王的城堡。此刻,蒟蒻勇者的心跳的飞快,因为他知道,他每向前走一步,当场去世的可能性就又增加了一分。
穿过幽长的走廊,我们的蒟蒻勇者终于见到了木薯魔王,并向他发出了挑战。“你想挑战我?”魔王笑了笑,“还蛊惑了我的咕咕鸡?看起来有点本事。这样吧,我和你下一盘蒟蒻棋,如果你赢了,我就把所有抢来的木薯还回去你看怎么样?”
蒟蒻勇者点了点头。“那么就听我讲讲这蒟蒻棋的规矩吧!”
「蒟蒻棋」是一种非常有趣的棋类游戏。大家都知道,围棋的「气」是指一个棋子所在的联通块相邻的空格。两粒棋如果在棋盘上线段的两端就认为是相邻的,也就是在同一个连通块里。比如在图中,白子为四个独立的连通块,黑子构成一个连通块,绿色点是黑子连通块唯一的「气」:
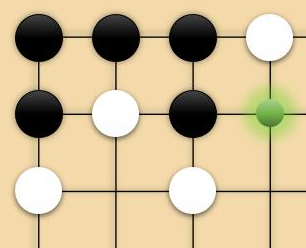
「提子」是指将没有「气」的棋子提出棋盘,在上图中,如果白方走绿点,那么就可以将黑子全部提走。
在普通围棋中,我们想尽量多地占领地盘、提走对方棋子。然而,蒟蒻棋恰恰相反——蒟蒻棋是一种非常和平的游戏,双方的走子不能产生任何提子,也就是说,任何一次走子不能让棋盘上任何一个棋子所在的连通块没有气。比如,白方在上图中不能走绿点。
在你的某一步棋后,对方无棋可走,那么你就赢了。
给你一个 n*n的棋盘,上面或许已经有一些棋子了,但此时局面一定是合法的,即不存在没有气的连通块;此时轮到黑棋下棋,因此棋盘上黑白棋子的数量一定是相等的。
你的任务是,依次为黑棋和白棋随意指定一个可行的走子位置,直到某一步游戏无法进行,决出胜负为止。
在正式的蒟蒻棋比赛还存在一些禁手规则。不过由于木薯魔王玩的是一种棋盘大小可变的新型不围棋,我们只用考虑上面提到的气的规则就好。
【输入格式】
从文件konjacchess.in中读入数据。
输入一行一个整数 n,表示棋盘大小。输入接下来 n行,每行有一个长度为 n的字符串,表示第 i 行的情况。
. 表示空X 表示黑棋O 表示白棋
详细请参考样例。
输入保证,棋盘初始局面合法,X 与 O 数量相等。
【输出格式】
输出到文件konjacchess.out中。
你需要输出至少一行,假设你输出了 L 行,那么对于前 L - 1 行,你应该输出两个用空格分隔的正整数表示下棋坐标 xi,yi其中奇数行表示黑棋的行动,偶数行表示白棋的行动。x 坐标为从上到下从 1 到 n,y 坐标为从左到右从 1 到 n。
请在第 L 行输出 -1 -1,表示此时第 L 手执棋人已经无棋可走。
你的输出可能会很大,即使本题时限为 1.5s,也请你不要使用太慢的方法输出大量内容。
【评分方式】
本题启用 Special Judge,没有部分分。我们将通过以下方式进行计分:
如果你输出格式错误,那么该测试点不得分。格式错误包括但不限于:输出了非数字内容;一行输出了超过或者少于两个正整数;输出的坐标在棋盘外;最后一行的输出不是 -1 -1。
如果你的输出格式正确,但是你的输出的某一行的答案就是不可接受的,那么该测试点不得分。例如:输出的坐标是黑棋不可以下的位置;黑棋有棋可走却输出了 -1 -1。
如果你的输出完全正确,无论你输出了多少行,你都将得到 10 分。
【样例 1 输入】
3
XXX
OOX
OO.
【样例 1 输出】
-1 -1
【样例2输入】
3
XOO
XO.
X..
【样例2输出】
2 3
-1 -1
解题思路
这道题作为DAY1的压轴题还是有一定的细节和码量的,考验的就是选手的码力和对细节的考量。其实思路是很简单的,我们只要在每一步下棋的时候,在我们还没有下的点当中选一个可行点下就行了,当下不下去的时候就结束程序,下面我们就来详细讲讲怎么操作。
很显然,我们的下棋程序主要分为两大部分:判断能否下和下下去后状态的维护,我们一点一点来解决。
首先我们先要开一个并查集f[i]j,其中要维护两个东西——一个是棋盘上(i,j)这个点所在哪个并查集——这个用记录父亲的方式就能很容易的记录和合并了;另一个是我们现在所在的并查集还有哪几格气(注意是哪几格气不是几格气),这个直接用set就行了。我们以现在要下黑棋为例子,我们如何判断现在的这个点(i,j)能不能下这个黑棋呢?很简单,我们只要判断三个东西——会不会让周围的白棋的气变成0,会不会让周围的黑棋的气变成0,会不会周围四个都是白棋,我一下下去就当场去世。如果这些条件都合法,那就代表这个点(i,j)是可以下的,具体判断直接用并查集就可以了。
接着考虑下下去以后如何维护状态。这也分为三步,首先先将该点构造成一个独立的并查集(维护好附近有哪几格气),接着将与他相连的联通块中去掉这个格子的气块(因为下了这个棋,这个格子就不是空的了,当然也就不是气了),最后将该格子和上下左右的同色块合并在一起就可以啦。
本题的难点主要在于细节的处理和选手的调试能力。难度定在提高+/省选。
程序实现
#include<set>
#include<cmath>
#include<queue>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
int a[660][660];char s[660];
int i,j,k,m,n,o,p,js,jl,jk,color,x,y,pd;
struct node
{
int fa;
set<int>q;
}f[600000];
int my_min(int x,int y)
{
if(x<y)return(x);
else return(y);
}
queue<int>jvruo;
int find(int u)
{
if(f[u].fa!=u)
{
f[u].fa=find(f[u].fa);
return(f[u].fa);
}
return(u);
}
int mer(int u,int v)
{
int uu=find(u),vv=find(v);
if(f[vv].q.size()<f[uu].q.size())swap(vv,uu);
f[uu].fa=vv;
f[vv].q.insert(f[uu].q.begin(),f[uu].q.end());
return 0;
}
int main()
{
FILE *fin,*fout;
fin=fopen("konjacchess.in","rb");
fout=fopen("konjacchess.out","wb");
fscanf(fin,"%d",&n);
memset(a,63,sizeof(a));
for(int i=1;i<=n;i++)
{
fscanf(fin,"%s",s+1);
for(int j=1;j<=n;j++)
{
if(s[j]=='X')a[i][j]=2;
if(s[j]=='O')a[i][j]=1;
if(s[j]=='.')
{
a[i][j]=0;
jvruo.push(i*n+j);
}
f[i*n+j].fa=i*n+j;
}
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
if(a[i][j]==1)
{
js=0;
if(a[i-1][j]==0)f[i*n+j].q.insert((i-1)*n+j);
if(a[i+1][j]==0)f[i*n+j].q.insert((i+1)*n+j);
if(a[i][j-1]==0)f[i*n+j].q.insert(i*n+j-1);
if(a[i][j+1]==0)f[i*n+j].q.insert(i*n+j+1);
if(a[i-1][j]==1 && a[i][j-1]!=1)mer(i*n+j,(i-1)*n+j);
if(a[i-1][j]!=1 && a[i][j-1]==1)mer(i*n+j,i*n+j-1);
if(a[i-1][j]==1 && a[i][j-1]==1)
{
mer(i*n+j,i*n+j-1);
mer(i*n+j,(i-1)*n+j);
}
}
if(a[i][j]==2)
{
js=0;
if(a[i-1][j]==0)f[i*n+j].q.insert((i-1)*n+j);
if(a[i+1][j]==0)f[i*n+j].q.insert((i+1)*n+j);
if(a[i][j-1]==0)f[i*n+j].q.insert(i*n+j-1);
if(a[i][j+1]==0)f[i*n+j].q.insert(i*n+j+1);
if(a[i-1][j]==2 && a[i][j-1]!=2)mer(i*n+j,(i-1)*n+j);
if(a[i-1][j]!=2 && a[i][j-1]==2)mer(i*n+j,i*n+j-1);
if(a[i-1][j]==2 && a[i][j-1]==2)
{
mer(i*n+j,i*n+j-1);
mer(i*n+j,(i-1)*n+j);
}
}
}
jl=n*n+1;color=1;
while(jl>jvruo.size())
{
color=3-color;
jl=jvruo.size();
for(int i=1;i<=jvruo.size();i++)
{
o=jvruo.front();
jvruo.pop();
x=o/n;y=o%n;
if(y==0)
{
y=n;
x--;
}
if(color==1)
{
js=5;pd=0;
if(x-1>0)if(a[x-1][y]==2)js=my_min(js,f[find((x-1)*n+y)].q.size());
if(x+1<=n)if(a[x+1][y]==2)js=my_min(js,f[find((x+1)*n+y)].q.size());
if(y-1>0)if(a[x][y-1]==2)js=my_min(js,f[find(x*n+y-1)].q.size());
if(y+1<=n)if(a[x][y+1]==2)js=my_min(js,f[find(x*n+y+1)].q.size());
if(js<=1)pd=1;//判断会不会堵住异色棋
if(pd==0)
{
if(x==1 || a[x-1][y]==2)
if(x==n || a[x+1][y]==2)
if(y==1 || a[x][y-1]==2)
if(y==n || a[x][y+1]==2)
pd=1;
} //判断会不会当场去世
if(pd==0)
{
js=0;
if(x-1>0)if(a[x-1][y]==1)js=(js+f[find((x-1)*n+y)].q.size())-1;
if(x+1<=n)if(a[x+1][y]==1)js=(js+f[find((x+1)*n+y)].q.size())-1;
if(y-1>0)if(a[x][y-1]==1)js=(js+f[find(x*n+y-1)].q.size())-1;
if(y+1<=n)if(a[x][y+1]==1)js=(js+f[find(x*n+y+1)].q.size())-1;
if(a[x-1][y]==0)js++;
if(a[x+1][y]==0)js++;
if(a[x][y-1]==0)js++;
if(a[x][y+1]==0)js++;
if(js<=0)pd=1;
}//判断会不会堵住同色棋
if(pd==0)
{
a[x][y]=1;
js=0;
if(a[x-1][y]==0)f[x*n+y].q.insert((x-1)*n+y);
if(a[x+1][y]==0)f[x*n+y].q.insert((x+1)*n+y);
if(a[x][y-1]==0)f[x*n+y].q.insert(x*n+y-1);
if(a[x][y+1]==0)f[x*n+y].q.insert(x*n+y+1);
if(x-1>0)if(a[x-1][y]>0)f[find((x-1)*n+y)].q.erase(x*n+y);
if(x+1<=n)if(a[x+1][y]>0)f[find((x+1)*n+y)].q.erase(x*n+y);
if(y-1>0)if(a[x][y-1]>0)f[find(x*n+y-1)].q.erase(x*n+y);
if(y+1<=n)if(a[x][y+1]>0)f[find(x*n+y+1)].q.erase(x*n+y);
if(x-1>0)if(a[x-1][y]==1)mer(x*n+y,(x-1)*n+y);
if(x+1<=n)if(a[x+1][y]==1)mer(x*n+y,(x+1)*n+y);
if(y-1>0)if(a[x][y-1]==1)mer(x*n+y,x*n+y-1);
if(y+1<=n)if(a[x][y+1]==1)mer(x*n+y,x*n+y+1);
fprintf(fout,"%d %d\n",x,y);
}//维护下下去后的状态
else jvruo.push(o);
}
if(color==1 && pd==0)break;
if(color==2)
{
js=5;pd=0;
if(x-1>0)if(a[x-1][y]==1)js=my_min(js,f[find((x-1)*n+y)].q.size());
if(x+1<=n)if(a[x+1][y]==1)js=my_min(js,f[find((x+1)*n+y)].q.size());
if(y-1>0)if(a[x][y-1]==1)js=my_min(js,f[find(x*n+y-1)].q.size());
if(y+1<=n)if(a[x][y+1]==1)js=my_min(js,f[find(x*n+y+1)].q.size());
if(js<=1)pd=1;//判断会不会堵住异色棋
if(pd==0)
{
if(x==1 || a[x-1][y]==1)
if(x==n || a[x+1][y]==1)
if(y==1 || a[x][y-1]==1)
if(y==n || a[x][y+1]==1)
pd=1;
} //判断会不会当场去世
if(pd==0)
{
js=0;
if(x-1>0)if(a[x-1][y]==2)js=(js+f[find((x-1)*n+y)].q.size())-1;
if(x+1<=n)if(a[x+1][y]==2)js=(js+f[find((x+1)*n+y)].q.size())-1;
if(y-1>0)if(a[x][y-1]==2)js=(js+f[find(x*n+y-1)].q.size())-1;
if(y+1<=n)if(a[x][y+1]==2)js=(js+f[find(x*n+y+1)].q.size())-1;
if(a[x-1][y]==0)js++;
if(a[x+1][y]==0)js++;
if(a[x][y-1]==0)js++;
if(a[x][y+1]==0)js++;
if(js<=0)pd=1;
}//判断会不会堵住同色棋
if(pd==0)
{
a[x][y]=2;
js=0;
if(a[x-1][y]==0)f[x*n+y].q.insert((x-1)*n+y);
if(a[x+1][y]==0)f[x*n+y].q.insert((x+1)*n+y);
if(a[x][y-1]==0)f[x*n+y].q.insert(x*n+y-1);
if(a[x][y+1]==0)f[x*n+y].q.insert(x*n+y+1);
if(x-1>0)if(a[x-1][y]>0)f[find((x-1)*n+y)].q.erase(x*n+y);
if(x+1<=n)if(a[x+1][y]>0)f[find((x+1)*n+y)].q.erase(x*n+y);
if(y-1>0)if(a[x][y-1]>0)f[find(x*n+y-1)].q.erase(x*n+y);
if(y+1<=n)if(a[x][y+1]>0)f[find(x*n+y+1)].q.erase(x*n+y);
if(x-1>0)if(a[x-1][y]==2)mer(x*n+y,(x-1)*n+y);
if(x+1<=n)if(a[x+1][y]==2)mer(x*n+y,(x+1)*n+y);
if(y-1>0)if(a[x][y-1]==2)mer(x*n+y,x*n+y-1);
if(y+1<=n)if(a[x][y+1]==2)mer(x*n+y,x*n+y+1);
fprintf(fout,"%d %d\n",x,y);
}//维护下下去后的状态
else jvruo.push(o);
}
if(color==2 && pd==0)break;
}
}
fprintf(fout,"-1 -1");
fclose(fin);
fclose(fout);
return 0;
}定义比较器的编写
这道题比题目更难的,是对于自定义比较器的编写。主要的思路就是先读入选手的输出文件,然后逐一判断是否操作合法,最后再跑一遍操作后的图,如果无法继续操作下去,则选手的答案是合法的。下面给出cena下的定义比较器的编写:
#include<set>
#include<cmath>
#include<queue>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
FILE *fscore,*freport,*fstd,*fin,*fout;
int a[660][660];char s[660];
int i,j,k,m,n,o,p,js,jl,jk,color,x,y,pd,pdd;
struct node
{
int fa;
set<int>q;
}f[600000];
int my_min(int x,int y)
{
if(x<y)return(x);
else return(y);
}
queue<int>jvruo;
int find(int u)
{
if(f[u].fa!=u)
{
f[u].fa=find(f[u].fa);
return(f[u].fa);
}
return(u);
}
int mer(int u,int v)
{
int uu=find(u),vv=find(v);
if(f[vv].q.size()<f[uu].q.size())swap(vv,uu);
f[uu].fa=vv;
f[vv].q.insert(f[uu].q.begin(),f[uu].q.end());
return 0;
}
int pf;
int Judge()
{
fscanf(fin,"%d",&n);
memset(a,63,sizeof(a));
for(int i=1;i<=n;i++)
{
fscanf(fin,"%s",s+1);
for(int j=1;j<=n;j++)
{
if(s[j]=='X')a[i][j]=2;
if(s[j]=='O')a[i][j]=1;
if(s[j]=='.')
{
a[i][j]=0;
}
f[i*n+j].fa=i*n+j;
}
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
if(a[i][j]==1)
{
js=0;
if(a[i-1][j]==0)f[i*n+j].q.insert((i-1)*n+j);
if(a[i+1][j]==0)f[i*n+j].q.insert((i+1)*n+j);
if(a[i][j-1]==0)f[i*n+j].q.insert(i*n+j-1);
if(a[i][j+1]==0)f[i*n+j].q.insert(i*n+j+1);
if(a[i-1][j]==1 && a[i][j-1]!=1)mer(i*n+j,(i-1)*n+j);
if(a[i-1][j]!=1 && a[i][j-1]==1)mer(i*n+j,i*n+j-1);
if(a[i-1][j]==1 && a[i][j-1]==1)
{
mer(i*n+j,i*n+j-1);
mer(i*n+j,(i-1)*n+j);
}
}
if(a[i][j]==2)
{
js=0;
if(a[i-1][j]==0)f[i*n+j].q.insert((i-1)*n+j);
if(a[i+1][j]==0)f[i*n+j].q.insert((i+1)*n+j);
if(a[i][j-1]==0)f[i*n+j].q.insert(i*n+j-1);
if(a[i][j+1]==0)f[i*n+j].q.insert(i*n+j+1);
if(a[i-1][j]==2 && a[i][j-1]!=2)mer(i*n+j,(i-1)*n+j);
if(a[i-1][j]!=2 && a[i][j-1]==2)mer(i*n+j,i*n+j-1);
if(a[i-1][j]==2 && a[i][j-1]==2)
{
mer(i*n+j,i*n+j-1);
mer(i*n+j,(i-1)*n+j);
}
}
}
fscanf(fout,"%d%d",&x,&y);
color=1;
while(x!=-1 && y!=-1)
{
color=3-color;
pdd=0;
for(int i=1;i<=1;i++)
{
if(color==1)
{
js=5;pd=0;
if(x-1>0)if(a[x-1][y]==2)js=my_min(js,f[find((x-1)*n+y)].q.size());
if(x+1<=n)if(a[x+1][y]==2)js=my_min(js,f[find((x+1)*n+y)].q.size());
if(y-1>0)if(a[x][y-1]==2)js=my_min(js,f[find(x*n+y-1)].q.size());
if(y+1<=n)if(a[x][y+1]==2)js=my_min(js,f[find(x*n+y+1)].q.size());
if(js<=1)pd=1;
if(pd==0)
{
if(x==1 || a[x-1][y]==2)
if(x==n || a[x+1][y]==2)
if(y==1 || a[x][y-1]==2)
if(y==n || a[x][y+1]==2)
pd=1;
}
if(pd==0)
{
js=0;
if(x-1>0)if(a[x-1][y]==1)js=(js+f[find((x-1)*n+y)].q.size())-1;
if(x+1<=n)if(a[x+1][y]==1)js=(js+f[find((x+1)*n+y)].q.size())-1;
if(y-1>0)if(a[x][y-1]==1)js=(js+f[find(x*n+y-1)].q.size())-1;
if(y+1<=n)if(a[x][y+1]==1)js=(js+f[find(x*n+y+1)].q.size())-1;
if(a[x-1][y]==0)js++;
if(a[x+1][y]==0)js++;
if(a[x][y-1]==0)js++;
if(a[x][y+1]==0)js++;
if(js<=0)pd=1;
}
if(pd==0)
{
a[x][y]=1;
js=0;
if(a[x-1][y]==0)f[x*n+y].q.insert((x-1)*n+y);
if(a[x+1][y]==0)f[x*n+y].q.insert((x+1)*n+y);
if(a[x][y-1]==0)f[x*n+y].q.insert(x*n+y-1);
if(a[x][y+1]==0)f[x*n+y].q.insert(x*n+y+1);
if(x-1>0)if(a[x-1][y]>0)f[find((x-1)*n+y)].q.erase(x*n+y);
if(x+1<=n)if(a[x+1][y]>0)f[find((x+1)*n+y)].q.erase(x*n+y);
if(y-1>0)if(a[x][y-1]>0)f[find(x*n+y-1)].q.erase(x*n+y);
if(y+1<=n)if(a[x][y+1]>0)f[find(x*n+y+1)].q.erase(x*n+y);
if(x-1>0)if(a[x-1][y]==1)mer(x*n+y,(x-1)*n+y);
if(x+1<=n)if(a[x+1][y]==1)mer(x*n+y,(x+1)*n+y);
if(y-1>0)if(a[x][y-1]==1)mer(x*n+y,x*n+y-1);
if(y+1<=n)if(a[x][y+1]==1)mer(x*n+y,x*n+y+1);
pdd=1;
}
else jvruo.push(o);
}
if(color==1 && pd==0)break;
if(color==2)
{
js=5;pd=0;
if(x-1>0)if(a[x-1][y]==1)js=my_min(js,f[find((x-1)*n+y)].q.size());
if(x+1<=n)if(a[x+1][y]==1)js=my_min(js,f[find((x+1)*n+y)].q.size());
if(y-1>0)if(a[x][y-1]==1)js=my_min(js,f[find(x*n+y-1)].q.size());
if(y+1<=n)if(a[x][y+1]==1)js=my_min(js,f[find(x*n+y+1)].q.size());
if(js<=1)pd=1;
if(pd==0)
{
if(x==1 || a[x-1][y]==1)
if(x==n || a[x+1][y]==1)
if(y==1 || a[x][y-1]==1)
if(y==n || a[x][y+1]==1)
pd=1;
}
if(pd==0)
{
js=0;
if(x-1>0)if(a[x-1][y]==2)js=(js+f[find((x-1)*n+y)].q.size())-1;
if(x+1<=n)if(a[x+1][y]==2)js=(js+f[find((x+1)*n+y)].q.size())-1;
if(y-1>0)if(a[x][y-1]==2)js=(js+f[find(x*n+y-1)].q.size())-1;
if(y+1<=n)if(a[x][y+1]==2)js=(js+f[find(x*n+y+1)].q.size())-1;
if(a[x-1][y]==0)js++;
if(a[x+1][y]==0)js++;
if(a[x][y-1]==0)js++;
if(a[x][y+1]==0)js++;
if(js<=0)pd=1;
}
if(pd==0)
{
a[x][y]=2;
js=0;
if(a[x-1][y]==0)f[x*n+y].q.insert((x-1)*n+y);
if(a[x+1][y]==0)f[x*n+y].q.insert((x+1)*n+y);
if(a[x][y-1]==0)f[x*n+y].q.insert(x*n+y-1);
if(a[x][y+1]==0)f[x*n+y].q.insert(x*n+y+1);
if(x-1>0)if(a[x-1][y]>0)f[find((x-1)*n+y)].q.erase(x*n+y);
if(x+1<=n)if(a[x+1][y]>0)f[find((x+1)*n+y)].q.erase(x*n+y);
if(y-1>0)if(a[x][y-1]>0)f[find(x*n+y-1)].q.erase(x*n+y);
if(y+1<=n)if(a[x][y+1]>0)f[find(x*n+y+1)].q.erase(x*n+y);
if(x-1>0)if(a[x-1][y]==2)mer(x*n+y,(x-1)*n+y);
if(x+1<=n)if(a[x+1][y]==2)mer(x*n+y,(x+1)*n+y);
if(y-1>0)if(a[x][y-1]==2)mer(x*n+y,x*n+y-1);
if(y+1<=n)if(a[x][y+1]==2)mer(x*n+y,x*n+y+1);
pdd=1;
}
else jvruo.push(o);
}
if(color==2 && pd==0)break;
}
fscanf(fout,"%d%d",&x,&y);
if(pdd==0)return(0);
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
if(a[i][j]==0)jvruo.push(i*n+j);
}
jl=n*n+1;
while(jl>jvruo.size())
{
color=3-color;
jl=jvruo.size();
for(int i=1;i<=jvruo.size();i++)
{
o=jvruo.front();
jvruo.pop();
x=o/n;y=o%n;
if(y==0)
{
y=n;
x--;
}
if(color==1)
{
js=5;pd=0;
if(x-1>0)if(a[x-1][y]==2)js=my_min(js,f[find((x-1)*n+y)].q.size());
if(x+1<=n)if(a[x+1][y]==2)js=my_min(js,f[find((x+1)*n+y)].q.size());
if(y-1>0)if(a[x][y-1]==2)js=my_min(js,f[find(x*n+y-1)].q.size());
if(y+1<=n)if(a[x][y+1]==2)js=my_min(js,f[find(x*n+y+1)].q.size());
if(js<=1)pd=1;
if(pd==0)
{
if(x==1 || a[x-1][y]==2)
if(x==n || a[x+1][y]==2)
if(y==1 || a[x][y-1]==2)
if(y==n || a[x][y+1]==2)
pd=1;
}
if(pd==0)
{
js=0;
if(x-1>0)if(a[x-1][y]==1)js=(js+f[find((x-1)*n+y)].q.size())-1;
if(x+1<=n)if(a[x+1][y]==1)js=(js+f[find((x+1)*n+y)].q.size())-1;
if(y-1>0)if(a[x][y-1]==1)js=(js+f[find(x*n+y-1)].q.size())-1;
if(y+1<=n)if(a[x][y+1]==1)js=(js+f[find(x*n+y+1)].q.size())-1;
if(a[x-1][y]==0)js++;
if(a[x+1][y]==0)js++;
if(a[x][y-1]==0)js++;
if(a[x][y+1]==0)js++;
if(js<=0)pd=1;
}
if(pd==0)
{
a[x][y]=1;
js=0;
if(a[x-1][y]==0)f[x*n+y].q.insert((x-1)*n+y);
if(a[x+1][y]==0)f[x*n+y].q.insert((x+1)*n+y);
if(a[x][y-1]==0)f[x*n+y].q.insert(x*n+y-1);
if(a[x][y+1]==0)f[x*n+y].q.insert(x*n+y+1);
if(x-1>0)if(a[x-1][y]>0)f[find((x-1)*n+y)].q.erase(x*n+y);
if(x+1<=n)if(a[x+1][y]>0)f[find((x+1)*n+y)].q.erase(x*n+y);
if(y-1>0)if(a[x][y-1]>0)f[find(x*n+y-1)].q.erase(x*n+y);
if(y+1<=n)if(a[x][y+1]>0)f[find(x*n+y+1)].q.erase(x*n+y);
if(x-1>0)if(a[x-1][y]==1)mer(x*n+y,(x-1)*n+y);
if(x+1<=n)if(a[x+1][y]==1)mer(x*n+y,(x+1)*n+y);
if(y-1>0)if(a[x][y-1]==1)mer(x*n+y,x*n+y-1);
if(y+1<=n)if(a[x][y+1]==1)mer(x*n+y,x*n+y+1);
return(0);
}
else jvruo.push(o);
}
if(color==1 && pd==0)break;
if(color==2)
{
js=5;pd=0;
if(x-1>0)if(a[x-1][y]==1)js=my_min(js,f[find((x-1)*n+y)].q.size());
if(x+1<=n)if(a[x+1][y]==1)js=my_min(js,f[find((x+1)*n+y)].q.size());
if(y-1>0)if(a[x][y-1]==1)js=my_min(js,f[find(x*n+y-1)].q.size());
if(y+1<=n)if(a[x][y+1]==1)js=my_min(js,f[find(x*n+y+1)].q.size());
if(js<=1)pd=1;
if(pd==0)
{
if(x==1 || a[x-1][y]==1)
if(x==n || a[x+1][y]==1)
if(y==1 || a[x][y-1]==1)
if(y==n || a[x][y+1]==1)
pd=1;
}
if(pd==0)
{
js=0;
if(x-1>0)if(a[x-1][y]==2)js=(js+f[find((x-1)*n+y)].q.size())-1;
if(x+1<=n)if(a[x+1][y]==2)js=(js+f[find((x+1)*n+y)].q.size())-1;
if(y-1>0)if(a[x][y-1]==2)js=(js+f[find(x*n+y-1)].q.size())-1;
if(y+1<=n)if(a[x][y+1]==2)js=(js+f[find(x*n+y+1)].q.size())-1;
if(a[x-1][y]==0)js++;
if(a[x+1][y]==0)js++;
if(a[x][y-1]==0)js++;
if(a[x][y+1]==0)js++;
if(js<=0)pd=1;
}
if(pd==0)
{
a[x][y]=2;
js=0;
if(a[x-1][y]==0)f[x*n+y].q.insert((x-1)*n+y);
if(a[x+1][y]==0)f[x*n+y].q.insert((x+1)*n+y);
if(a[x][y-1]==0)f[x*n+y].q.insert(x*n+y-1);
if(a[x][y+1]==0)f[x*n+y].q.insert(x*n+y+1);
if(x-1>0)if(a[x-1][y]>0)f[find((x-1)*n+y)].q.erase(x*n+y);
if(x+1<=n)if(a[x+1][y]>0)f[find((x+1)*n+y)].q.erase(x*n+y);
if(y-1>0)if(a[x][y-1]>0)f[find(x*n+y-1)].q.erase(x*n+y);
if(y+1<=n)if(a[x][y+1]>0)f[find(x*n+y+1)].q.erase(x*n+y);
if(x-1>0)if(a[x-1][y]==2)mer(x*n+y,(x-1)*n+y);
if(x+1<=n)if(a[x+1][y]==2)mer(x*n+y,(x+1)*n+y);
if(y-1>0)if(a[x][y-1]==2)mer(x*n+y,x*n+y-1);
if(y+1<=n)if(a[x][y+1]==2)mer(x*n+y,x*n+y+1);
return(0);
}
else jvruo.push(o);
}
if(color==2 && pd==0)break;
}
}
return(1);
}
int main(int argc,char *argv[])
{
fscore=fopen("score.log","w"); //打开得分文件
freport=fopen("report.log","w");//打开报告文件
fstd=fopen(argv[2],"r"); //打开测试点标准输出文件
int score=atoi(argv[1]); //取得测试点的分数
fin=fopen("konjacchess.in","r"); //打开测试点标准输入文件
fout=fopen("konjacchess.out","r"); //打开用户的数据输出文件
if (!fout)
{
fprintf(fscore,"%d",0); //返回0分
fprintf(freport,"没输出你交上来干啥");//报告Judge结果为no output
}
else if (Judge()==1) //Judge后结果为真
{
fprintf(fscore,"%d",score);//返回满分
fprintf(freport,"太厉害了,被你A了"); //报告Judge结果为right
}
else
{
fprintf(fscore,"%d",0); //返回0分
fprintf(freport,"你愉快地WA了");//报告Judge结果为wrong
}
fclose(fscore);//关闭得分文件
fclose(freport);//关闭报告文件
return 0;
} 结语
以上是 JROI DAY1 的题目和解析了,希望你能在这次模拟题中有所收获。最后希望你喜欢这篇BLOG!
确实……由于时间的关系这次的题目蛮多都是原题的……不过都是一些很有意思的题目,望谅解……不过自定义比较器是博主苦思冥想搞出来的QwQ
我看了一题叫不围棋的和jvruo棋好像