这几天闲来无事去学习了一下计算几何,发现其实不($sang$)是($xin$)太($bing$)难($kuang$)
今天就重点介绍一下简单的叉积及其简单的运用(毕竟作为蒟蒻,难的搞不来啊)
什么是计算几何?
“对几何外形信息的计算机表示、分析和综合”——福雷斯特
其实所谓计算几何,就是用计算机去解决不同维度上的几何问题,而我们要做的,就是设计一套算法,让计算机去分析和解决一系列的几何问题。
一些基本知识
坐标的存储
一般来说,计算几何都涉及到了小数坐标,这时开一个含两个 $double$ 类型的结构体就比较稳健,我一般的定义如下:
struct node { //定义一个点
double x, y;
}a[11000];线段的存储
聪明绝顶的你肯定已经想到了,线段就是包含两个点的一个结构体,所以我一般的定义如下
struct line { //定义一条线
node p1, p2;
}list[11000];叉积
终于到今天的主角—叉积了!
那么什么是叉积呢?叉积其实是两个矢量模的乘积再乘夹角正弦,经过推导可以发现两个向量$A(x_1,y_1)$,$B(x_2,y_2)$的叉积为:$x_1 * y_2 - x_2 * y_1$,先丢出代码:
double multi(node p1, node p2, node p0) { //计算叉积,p1,p2,p0都为点
double x1, y1, x2, y2;
x1 = p1.x - p0.x;
y1 = p1.y - p0.y;
x2 = p2.x - p0.x;
y2 = p2.y - p0.y;
return x1 * y2 - x2 * y1;
}这就是传说中的叉积计算了!是不是很短呢,那就让我们来理解一下这个 $multi$ 函数吧。
由于叉积是向量间的运算,大家都知道向量可以用末坐标减去首坐标得到,那么其实 $multi$ 函数计算的就是向量 $A(x1,y1)$ 与向量 $B(x2,y2)$ 的叉积。
对于 $multi$ 函数的意义,首先 $multi$ 的正负是有特殊含义的:以 $p_0$ 为参考点,如果 $multi$ 大于 $0$,则 $p_2$ 在 $p_1$ 的逆时针方向,反正,如果 $multi$ 小于 $0$,则 $p_2$ 在 $p_1$的顺时针方向,特殊的,当 $multi$ 等于 $0$,$p_1$、$p_2$、$p_0$ 三点共线。
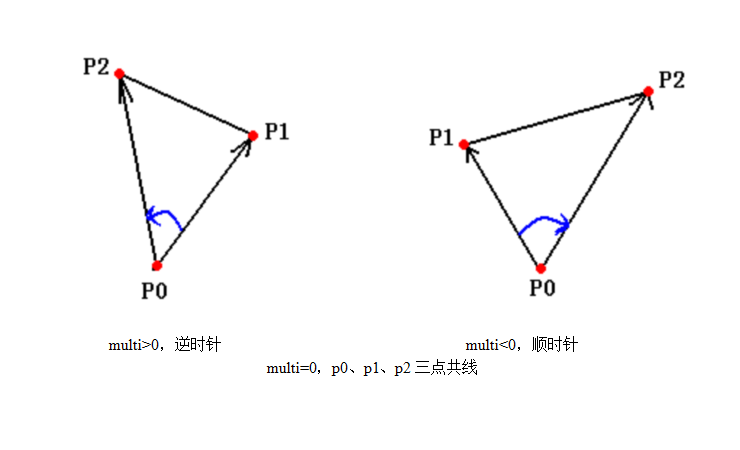
其次,$multi$ 的值也是有含义的!通过后面的学习你就会发现,$multi$ 的绝对值就是以 $p_0$、$p_1$、$p_2$ 三点构成的三角形的面积的两倍!利用这个规律,可以完成很多与计算几何有关的题目。
一些简单的运用
[caioj1212]判断线段相交(跨立实验)
题目描述
问题描述
有 $n$ 条线段(编号为 $1$ ~ $n$),按 $1$ ~ $n$ 的顺序放在二维坐标系上(就是先放 $1$ 号,再放 $2$ 号……),
要求输出最上面的那些线段的编号(就是没有其他线段压在它上面的那些线段)
输入格式
第一行第一个数 $n(1 \le n \le 10000)$表示这组数据有 $n$ 条线段。
接下来 $n$ 行,每行两个坐标,表示第i条线段的两个端点。
输出格式
输出一行。输出最上面的线段的编号(从小到大)。相邻两个编号用空格隔开,最后一个编号没有空格。
样例输入输出
【样例1输入】
5
1 1 4 2
2 3 3 1
1 -2.0 8 4
1 4 8 2
3 3 6 -2.0【样例1输出】
2 4 5【样例2输入】
3
0 0 1 1
1 0 2 1
2 0 3 1【样例2输出】
1 2 3解题思路
这道题很明显要让我们判断任意两条线段是否相交,这就要用到刚刚讲到的叉积的第一种用法了!
很明显,相交有两种情况,相交且穿过和相交但不穿过(如下图)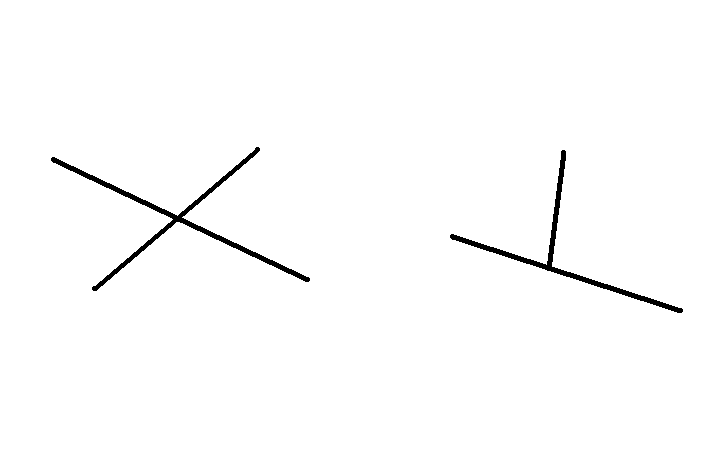
我们首先先讨论第一种情况,如何判断两条直线相交且穿过?

如上图,先假设两条直线为 $L_1$ 和 $L_2$,每条直线的两个端点分别为 $p_1$ 和 $p_2$,那么如果以
$L_1.p_1$为一个参考点,如果 $L_1.p_2$ 在 $L2.p1$ 与 $L_2.p_2$ 中间;再以 $L_2.p_1$ 为参考点,如果 $L_2.p_2$ 在 $L_1.p_1$ 与 $L_1.p_2$ 中间,那么就可以判断 $L_1$ 与 $L_2$ 相交且穿过(如下图)
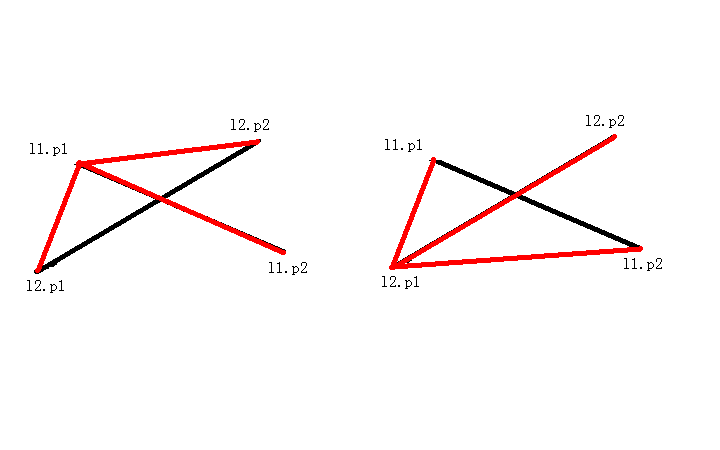
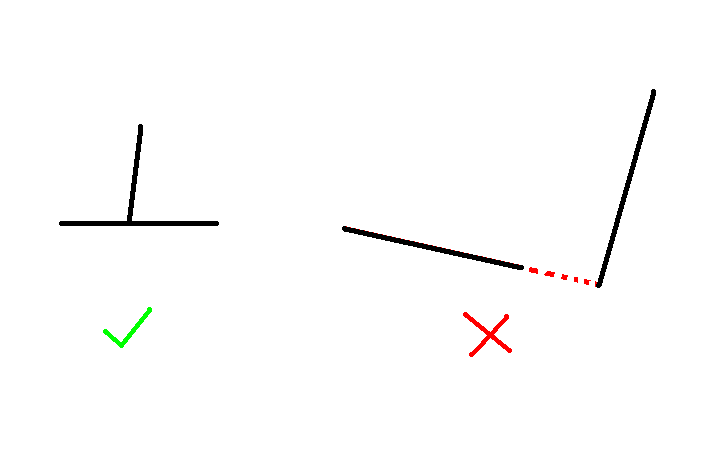
这种情况非常好理解吧,下一种情况就更加简单了,仅需讨论哪三个点在一条“直线”上(毕竟不穿过,所以必有三点共线),然后判断一下
不穿过的那个点是否在一条“线段”上(如下图)
具体代码如下
double check(line l1, line l2) { //判断是否相交
if(multi(l2.p1, l1.p2, l1.p1) * multi(l1.p2, l2.p2, l1.p1) > 0)//判断以L1.p1为基准,L1.p2是否在L2.p1与L2.p2中间
if(multi(l1.p1, l2.p2, l2.p1) * multi(l2.p2, l1.p2, l2.p1) > 0)//判断以L2.p1为基准,L2.p2是否在L1.p1与L2.p2中间
return true;//大部分情况下,能判断两直线相交
if(multi(l1.p1, l1.p2, l2.p1) == 0) if(mymin(l1.p1.x, l1.p2.x) <= l2.p1.x) if(mymax(l1.p1.x, l1.p2.x) >= l2.p1.x) if(mymin(l1.p1.y, l1.p2.y) <= l2.p1.y) if(mymax(l1.p1.y, l1.p2.y) >= l2.p1.y) return true;
if(multi(l1.p1, l1.p2, l2.p2) == 0) if(mymin(l1.p1.x, l1.p2.x) <= l2.p2.x) if(mymax(l1.p1.x, l1.p2.x) >= l2.p2.x) if(mymin(l1.p1.y, l1.p2.y) <= l2.p2.y) if(mymax(l1.p1.y, l1.p2.y) >= l2.p2.y) return true;
if(multi(l2.p1, l2.p2, l1.p1) == 0) if(mymin(l2.p1.x, l2.p2.x) <= l1.p1.x) if(mymax(l2.p1.x, l2.p2.x) >= l1.p1.x) if(mymin(l2.p1.y, l2.p2.y) <= l1.p1.y) if(mymax(l2.p1.y, l2.p2.y) >= l1.p1.y) return true;
if(multi(l2.p1, l2.p2, l1.p2) == 0) if(mymin(l2.p1.x, l2.p2.x) <= l1.p2.x) if(mymax(l2.p1.x, l2.p2.x) >= l1.p2.x) if(mymin(l2.p1.y, l2.p2.y) <= l1.p2.y) if(mymax(l2.p1.y, l2.p2.y) >= l1.p2.y) return true;
//判断两条直线相交且一条直线端点在另一条直线上
return false;
}在之前的版本里,我在判断两条直线相交且一条直线端点在另一条直线上的情况中忽略了两条直线互相一条与 $x$ 轴垂直,一条与 $y$ 轴垂直,且某一条延伸出去恰好交于另一条直线交点的情况,于是在一次比赛中 $WA$ 了十多发 $QwQ$,下面放上错误代码以作为警示:
double check(line l1, line l2) { //判断是否相交
if(multi(l2.p1, l1.p2, l1.p1) * multi(l1.p2, l2.p2, l1.p1) > 0)//判断以L1.p1为基准,L1.p2是否在L2.p1与L2.p2中间
if(multi(l1.p1, l2.p2, l2.p1) * multi(l2.p2, l1.p2, l2.p1) > 0)//判断以L2.p1为基准,L2.p2是否在L1.p1与L2.p2中间
return true;//大部分情况下,能判断两直线相交 if(multi(l2.p1,l1.p1,l1.p2)==0)if(mymin(l1.p1.x,l1.p2.x<=l2.p1.x)if(mymax(l1.p1.x,l1.p2.x)>=l2.p1.x)return true;
if(multi(l2.p1, l1.p1, l1.p2) == 0) if(mymin(l1.p1.x, l1.p2.x) <= l2.p1.x) if(mymax(l1.p1.x, l1.p2.x) >= l2.p1.x) return true;
if(multi(l2.p2, l1.p1, l1.p2) == 0) if(mymin(l1.p1.x, l1.p2.x) <= l2.p2.x) if(mymax(l1.p1.x, l1.p2.x) >= l2.p2.x) return true;
if(multi(l1.p1, l2.p1, l2.p2) == 0) if(mymin(l2.p1.x, l2.p2.x) <= l1.p1.x) if(mymax(l2.p1.x, l2.p2.x) >= l1.p1.x) return true;
if(multi(l1.p2, l2.p1, l2.p2) == 0) if(mymin(l2.p1.x, l2.p2.x) <= l1.p2.x) if(mymax(l2.p1.x, l2.p2.x) >= l1.p2.x) return true;
//判断两条直线相交且一条直线端点在另一条直线上
return false;
}主程序就很简单了,一条一条边读入,读入第i条边时判断他与前 $i-1$ 条边是否相交,若相交,这之前的边j被盖住,判断数组 $bo[j]=1$。最后统计$bo[i]==0$ 的边就好啦,附上完整代码:
#include<cmath>
#include<cstdlib>
#include<cstdio>
#include<cstring>
using namespace std;
struct node { //定义一个点
double x, y;
};
struct line { //定义一条线
node p1, p2;
} list[11000];
int a[11000] = {0};
bool bo[11000] = {0};
int n, len;
//================================
double mymax(double x, double y) { //求max
if(x > y)return x;
else return y;
}
double mymin(double x, double y) { //求min
if(x < y)return x;
else return y;
}
//=================================
double multi(node p1, node p2, node p0) { //计算叉积,p1,p2,p0都为点
double x1, y1, x2, y2;
x1 = p1.x - p0.x;
y1 = p1.y - p0.y;
x2 = p2.x - p0.x;
y2 = p2.y - p0.y;
return x1 * y2 - x2 * y1;
}
double check(line l1, line l2) { //判断是否相交
if(multi(l2.p1, l1.p2, l1.p1) * multi(l1.p2, l2.p2, l1.p1) > 0)//判断以L1.p1为基准,L1.p2是否在L2.p1与L2.p2中间
if(multi(l1.p1, l2.p2, l2.p1) * multi(l2.p2, l1.p2, l2.p1) > 0)//判断以L2.p1为基准,L2.p2是否在L1.p1与L2.p2中间
return true;//大部分情况下,能判断两直线相交
if(multi(l1.p1, l1.p2, l2.p1) == 0) if(mymin(l1.p1.x, l1.p2.x) <= l2.p1.x) if(mymax(l1.p1.x, l1.p2.x) >= l2.p1.x) if(mymin(l1.p1.y, l1.p2.y) <= l2.p1.y) if(mymax(l1.p1.y, l1.p2.y) >= l2.p1.y) return true;
if(multi(l1.p1, l1.p2, l2.p2) == 0) if(mymin(l1.p1.x, l1.p2.x) <= l2.p2.x) if(mymax(l1.p1.x, l1.p2.x) >= l2.p2.x) if(mymin(l1.p1.y, l1.p2.y) <= l2.p2.y) if(mymax(l1.p1.y, l1.p2.y) >= l2.p2.y) return true;
if(multi(l2.p1, l2.p2, l1.p1) == 0) if(mymin(l2.p1.x, l2.p2.x) <= l1.p1.x) if(mymax(l2.p1.x, l2.p2.x) >= l1.p1.x) if(mymin(l2.p1.y, l2.p2.y) <= l1.p1.y) if(mymax(l2.p1.y, l2.p2.y) >= l1.p1.y) return true;
if(multi(l2.p1, l2.p2, l1.p2) == 0) if(mymin(l2.p1.x, l2.p2.x) <= l1.p2.x) if(mymax(l2.p1.x, l2.p2.x) >= l1.p2.x) if(mymin(l2.p1.y, l2.p2.y) <= l1.p2.y) if(mymax(l2.p1.y, l2.p2.y) >= l1.p2.y) return true;
//判断两条直线相交且一条直线端点在另一条直线上
return false;
}
//==================================
int main() {
scanf("%d", &n);
for(int i = 1; i <= n; i++) scanf("%lf%lf%lf%lf", &list[i].p1.x, &list[i].p1.y, &list[i].p2.x, &list[i].p2.y);
for(int i = 1; i < n; i++) {
for(int j = i + 1; j <= n; j++) {
if(check(list[i], list[j])) { //判断相交
bo[i] = 1;
break;
}
}
}
len = 0;
for(int i = 1; i <= n; i++) if(bo[i] == 0) a[++len] = i;
for(int i = 1; i < len; i++) printf("%d ", a[i]);
printf("%d\n", a[len]);
return 0;
}
[caioj1213]面积
题目描述
问题描述
在一个平面坐标系上随意画一条有 $n$ 个点的封闭折线(按画线的顺序给出点的坐标),保证封闭折线的任意两条边都不相交。最后要计算这条路线包围的面积。
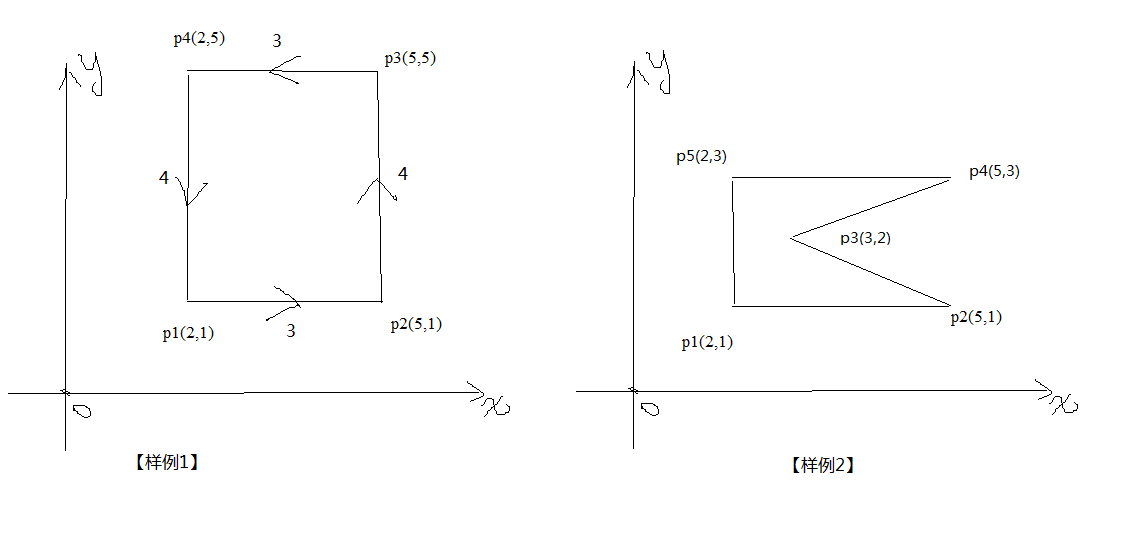
输入格式
第一行整数 $n (3 \le n \le 1000)$,表示有 $n$ 个点。
下来 $n$ 行,每行两个整数 $x$(横坐标)和$y$(纵坐标),表示点坐标$(-10000 < x,y \le 10000)$。
输出格式
一行一个实数,即封闭折线所包围的面积(保留 $4$ 位小数)。
样例输入输出
【样例1输入】
4
2 1
5 1
5 5
2 5【样例1输出】
12.0000【样例2输入】
5
2 1
5 1
3 2
5 3
2 3【样例2输出】
4.0000解题思路
这道题对比上一道题就简单很多了,这道题要用到叉积的第二种用法——计算面积!对于任意一个多边形,只要以一号点 $p_1$ 为参考点,枚举任意两个相邻的点 $p_i$ 和 $p_{i-1}(i>=3)$,带符号计算 $p_1$ 和 $p_i、p_{i-1}$所构成的三角形的面积($\frac{multi(p_i,p_{i-1},p_1)}{2}$),累加取绝对值就是答案了。
至于为什么要带符号运算,请看我用下面这幅图演示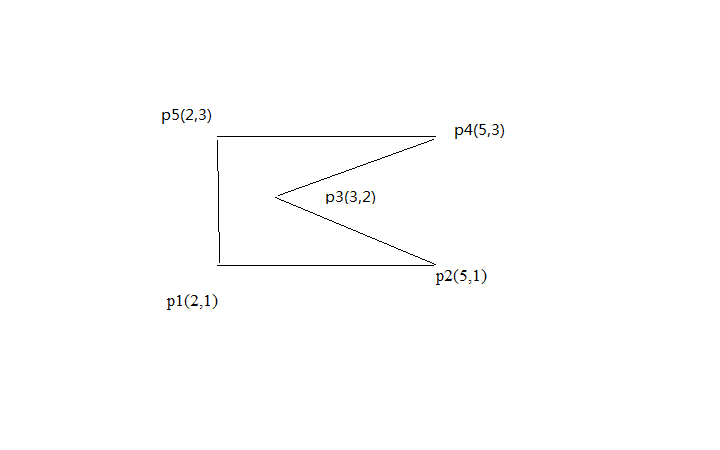
对于这个多边形,首先先加上 $\frac{multi(p_3,p_2,p_1)}{2}$ 的值(由于 $p_3$ 在 $p_2$ 的逆时针方向,所以为正)即为加上了红色部分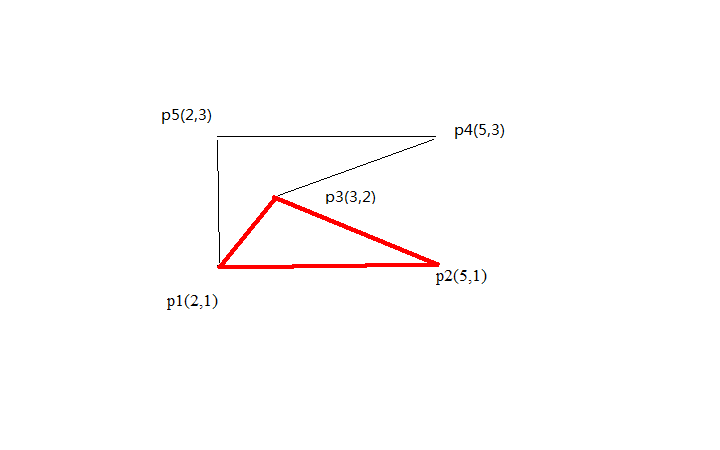
然后再加上 $\frac{multi(p_4,p_3,p_1)}{2}$ 的值(由于 $p_4$ 在 $p_3$ 的顺时针方向,所以为负)即为减去了绿色部分
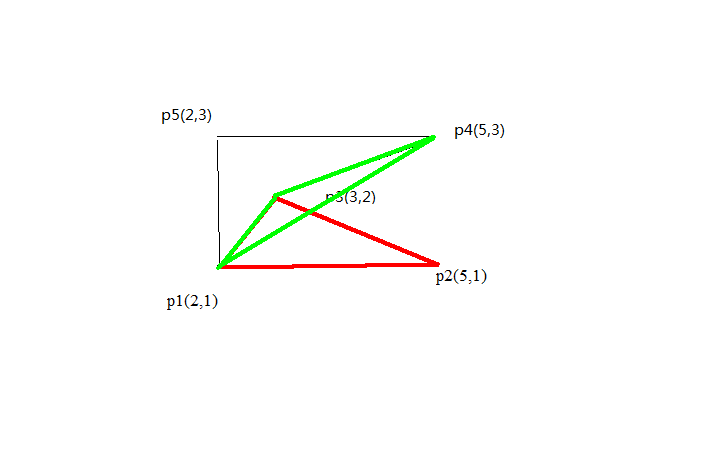
然后再加上 $\frac{multi(p_5,p_4,p_1)}{2}$ 的值(由于 $p_5$ 在 $p_4$ 的逆时针方向,所以为正)即为加上了黄色部分,就是答案了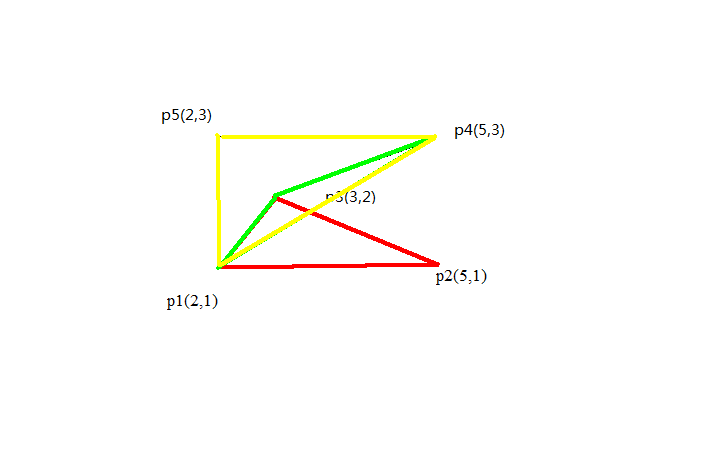
最后附上代码:
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
struct node {
double x, y;
} a[11000];
int n;
double ans;
double multi(node p1, node p2, node p0) { //计算叉积,p1,p2,p0都为点
double x1, y1, x2, y2;
x1 = p1.x - p0.x;
y1 = p1.y - p0.y;
x2 = p2.x - p0.x;
y2 = p2.y - p0.y;
return x1 * y2 - x2 * y1;
}
int main() {
scanf("%d", &n);
for(int i = 1; i <= n; i++) scanf("%lf%lf", &a[i].x, &a[i].y);
for(int i = 2; i <= n; i++) {
ans = ans + multi(a[i], a[i - 1], a[1]);
}
ans = ans / 2.0;
if(ans < 0) ans = -ans;
printf("%0.4lf", ans);
return 0;
}结语
通过上面的学习和例题,是不是已经初步了解了计算几何的一点点精(皮)髓(毛)呢,希望你能有所收获,在计算几何的路上越走越远吧(蒟蒻的我可能是走不下去了)
最后$Orz$各位大佬,写的不好请各位神犇提出建议和意见,感谢你的阅读!
受益匪浅
聪明绝♂顶?
我是博主的同学
这篇文章改变了我的一生。
当我在打lol时,看到了一个残血的人,我就冲上去,把他秒了,博主说我抢了他五杀,我说我抢了你吗比的五杀,我们吵了起来,后来我才知道,他身披国旗,是真的没有开挂。
(1)“三个代表”是我们的立党之本。我们党自成立之日起,就是走在中国社会发展前列的先进政党。我们的党章规定,中国共产党的中国工人阶级的先锋队。我们党的历史使命、历史地位、历史作用,始终是与党的先进性联系在一起的。什么时候坚持并做到了这样“三个代表”,我们党就兴旺发达,就得到人民群众的拥护,就经得起任何风浪的冲击。什么时候如果偏离或投有完全做到“三个代表”,就会出这样那样的问题,人民就会不满意,党就会遇到困难和曲折。
(2)“三个代表”是我们的执政之基。我们党的执政地位是历史赋予的、人民赋予的。我们党能够执政、并且能够执好政的基础,从根本上来说,就在于能够代表中国先进生产力的发展要求,代表中国先进文化的前进方向,代表中国:最广大人民的根本利益。我们党执政的内容和任务,就是要不断解放和发展中国社会的生产力,增强综合国力,推进社会发展;就是要不断建设和发展面向现代化、面向世界、面向未来的民族的、科学的、大众的社会主义文化,培育“四有”公民,弘扬民族精神;就是要全心全为人民服务,维护最广大人民的根本利益,不断满足人民群众日益增长的物质文化生活需要。面向新的世纪,我们党治国理政的任务更加艰巨,所要解决的问题也更多、更复杂。只有坚持“三个代表”,当好“三个代表”,我们才能始终用好人民赋予的执政权力,无愧于历史赋予的执政地位;才能不断提高我们的执政水平,巩固我们的执政基础。
(3)“三个代表”是我们的力量之源。我们党建党之初,只有几十个党员。为什么能够不断发展壮大,成为今天拥有6100多万党员的大党?为什么能够战胜曾经比自己强大得多的国内外敌人,建立起社会主义的新中国?为什么能够在一穷二白的基础上,取得经济和社会发展的巨大成就,解决了12亿人的温饱问题;在本世纪末进入了小康社会?为什么虽然也犯过错误,有过曲折,但始终“岁老根弥壮,阳骄叶更阴”,经得起各种风浪、磨难的考验,得到人民群众的拥护和支持?所有这一切,就是于我们党能够始终从根本上促进中国社会生产力的发展,推动中国文化的进步,切切实实地为人民办实事、谋利益。这是我们全部力量的源泉所在,也是我们不断成功和发展的奥秘所在。
我是博主女朋友
这篇博客改变了他的一生。
当我五杀被抢后,我非常绝望,去酒吧喝酒准备一醉不醒,这时,我遇见了他,他看了这篇博客后,学会了赚钱。他找到我后,和我***,之后我放弃了轻生的想法,成为了他的女朋友,虽然我被日后得知,他还有几万个女朋友,但我不在乎,因为他在我绝望的时候拯救了我。现在他回北大读书,我任然天天开他的劳斯莱斯去学校看望他,感觉人生变得如此幸福!!!
这篇博客改变了我的一生。
当我考上北大之后,因为学费交不起,没有办法去北京读书,我愤怒的撕掉了录取通知书,和小伙伴们去网吧电竞去了。这时候,小伙伴们介绍我上了jv%ruo%.co%m,不仅不花钱,学会了以后还能赚钱,不一会我就赚了几十亿,买了劳斯莱斯,找了七八十万个女朋友,北大校长都专门过来,请我回去读书。
感谢博主
Orz,太强了
博主让我10min就学会了计算几何!太厉害了
你搞的这个文章啊,Exited!
要提高姿势水平
Orz,太强了
Orz,Orz
Orz,太强了